2.5 Properties of the Derivative
In elementary calculus, we learn how to differentiate sums, products, quotients, and composite functions. We now generalize these ideas to functions of several variables, paying particular attention to the differentiation of composite functions. The rule for differentiating composites, called the chain rule, takes on a more profound form for functions of several variables than for those of one variable.
If \(f\) is a real-valued function of one variable, written as \(z = f(y)\), and \(y\) is a function of \(x\), written \(y= g(x)\), then \(z\) becomes a function of \(x\) through substitution, namely, \(z = f(g(x))\), and we have the familiar chain rule: \[ \frac{dz}{dx} = \frac{dz}{dy} \frac{dy}{dx} = f' (g(x)) g' (x). \]
If \(f\) is a real-valued function of three variables \(u,v\), and \(w\), written in the form \(z = f(u,v,w)\), and the variables \(u,v,w\) are each functions of \(x,u = g(x), v= h(x)\), and \(w = k (x)\), then by substituting \(g(x), h(x)\), and \(k (x)\) for \(u,v\), and \(w\), we obtain \(z\) as a function of \(x\colon\, z = f (g (x), h (x), k(x))\). The chain rule in this case reads: \[ \frac{dz}{dx} = \frac{\partial z}{\partial u} \frac{du}{dx} + \frac{\partial z}{\partial v} \frac{dv}{dx} + \frac{\partial z}{\partial w} \frac{dw}{dx}. \]
One of the goals of this section is to explain such formulas in detail.
Sums, Products, Quotients
These rules work just as they do in one-variable calculus.
125
Theorem 10 Sums, Products, Quotients
- (i) Constant Multiple Rule. Let \(f\colon\, U \subset {\mathbb R}^n \rightarrow {\mathbb R}^m\) be differentiable at \({\bf x}_0\) and let \(c\) be a real number. Then \(h ({\bf x}) = cf ( {\bf x})\) is differentiable at \({\bf x}_0\) and \[ {\bf D} h ( {\bf x}_0) = c {\bf D}\! f ( {\bf x}_0) \qquad \hbox{(equality of matrices)}. \]
- (ii) Sum Rule. Let \(f\colon\, U \subset {\mathbb R}^n \rightarrow {\mathbb R}^m\) and \(g\colon\, U \subset {\mathbb R}^n \rightarrow {\mathbb R}^m\) be differentiable at \({\bf x}_0\). Then \(h ( {\bf x}) = f ( {\bf x})+ g ( {\bf x})\) is differentiable at \({\bf x}_0\) and \[ {\bf D} h ( {\bf x}_0) = {\bf D}\! f ( {\bf x}_0) + {\bf D} g ( {\bf x}_0) \qquad \hbox{(sum of matrices).} \]
- (iii) Product Rule. Let \(f\colon\, U \subset {\mathbb R}^n \rightarrow {\mathbb R}\) and \(g\colon\, U \subset {\mathbb R}^n \rightarrow {\mathbb R}\) be differentiable at \({\bf x}_0\) and let \(h ( {\bf x}) = g ({\bf x}) f ({\bf x})\). Then \(h\colon\, U \subset {\mathbb R}^n \rightarrow {\mathbb R}\) is differentiable at \({\bf x}_0\) and \[ {\bf D} h ( {\bf x}_0 ) = g ( {\bf x}_0) {\bf D}\! f ( {\bf x}_0)+ f ( {\bf x}_0) {\bf D} g ( {\bf x}_0). \] (Note that each side of this equation is a \(1\times n\) matrix; a more general product rule is presented in Exercise \(31\) at the end of this section.)
- (iv) Quotient Rule. With the same hypotheses as in rule (iii), let \(h ( {\bf x}) = f ({\bf x}) / g ( {\bf x})\) and suppose \(g\) is never zero on \(U\). Then \(h\) is differentiable at \({\bf x}_0\) and \[ {\bf D} h ( {\bf x}_0) = \frac{ g ( {\bf x}_0) {\bf D}\! f ( {\bf x}_0) - f ( {\bf x}_0) {\bf D} g ( {\bf x}_0)}{ [ g ( {\bf x}_0)]^2} . \]
proof
The proofs of rules (i) through (iv) proceed almost exactly as in the one-variable case, with a slight difference in notation. We shall prove rules (i) and (ii), leaving the proofs of rules (iii) and (iv) as Exercise 27.
- (i) To show that \({\bf D} h ( {\bf x}_0) = c {\bf D}\! f ({\bf x}_0)\), we must show that \[ {\mathop {{\rm limit} }_{{\bf x} \to {\bf x}_0}} \ \frac{ \| h ( {\bf x} ) - h ( {\bf x}_0) - c {\bf D}\! f ( {\bf x}_0) ( {\bf x}- {\bf x}_0) \| }{ \| {\bf x} - {\bf x}_0 \| } =0, \] that is, that \[ {\mathop {{\rm limit} }_{{\bf x} \to {\bf x}_0}} \ \frac{ \| cf( {\bf x}) - cf( {\bf x}_0) - c {\bf D}\! f ( {\bf x}_0) ( {\bf x}- {\bf x}_0) \| }{ \| {\bf x} - {\bf x}_0 \| } =0, \] [see equation (4) of Section 2.3]. This is certainly true, since \(f\) is differentiable and the constant \(c\) can be factored out [see Theorem 3(i), Section 2.2].
- (ii) By the triangle inequality, we may write \begin{eqnarray*} &&\frac{ \| h ({\bf x}) - h ( {\bf x}_0) - [{\bf D}\! f ( {\bf x}_0) + {\bf D} g ({\bf x}_0) ] ( {\bf x}- {\bf x}_0) \| }{ \| {\bf x} - {\bf x}_0 \|} \\[3pt] && =\frac{ \| f({\bf x})-f({\bf x}_0)-[{\bf D}\! f({\bf x}_0)]({\bf x}-{\bf x}_0)+g({\bf x})-g({\bf x}_0)-[{\bf D}g({\bf x}_0)]({\bf x}-{\bf x}_0) \|}{\| {\bf x}-{\bf x}_0 \| } \\[3pt] && \leq \frac{ \| f({\bf x})-f({\bf x}_0)-[{\bf D}\! f({\bf x}_0)]({\bf x}-{\bf x}_0) \| }{ \| {\bf x}-{\bf x}_0 \| }+ \frac{ \| g({\bf x})-g({\bf x}_0)-[{\bf D}g({\bf x}_0)] ({\bf x}-{\bf x}_0) \| }{ \| {\bf x}-{\bf x}_0 \| }, \end{eqnarray*} and each term approaches 0 as \({\bf x}\rightarrow {\bf x}_0\). Hence, rule (ii) holds.
126
example 1
Verify the formula for \({\bf D}h\) in rule (iv) of Theorem 10 with \[ f(x,y,z)=x^2+y^2+z^2 \hbox{ and } g(x,y,z)=x^2+1. \]
solution Here \[ h(x,y,z)=\frac{x^2+y^2+z^2}{x^2+1}, \] so that by direct differentiation \begin{eqnarray*} {\bf D}h(x,y,z) &\!=\!& \bigg[\frac{\partial h}{\partial x},\frac{\partial h}{\partial y}, \frac{\partial h}{\partial z}\bigg] \!=\!\bigg[\frac{(x^2+1)2x-(x^2+y^2+z^2)2x}{(x^2+1)^2}, \frac{2y}{x^2+1},\frac{2z}{x^2+1}\bigg]\\[6pt] &=&\!\bigg[\frac{2x(1-y^2-z^2)}{(x^2+1)^2},\frac{2y}{x^2+1},\frac{2z}{x^2+1}\bigg]. \end{eqnarray*}
By rule (iv), we get \[ {\bf D}h=\frac{g{\bf D}\! f-f{\bf D}g}{g^2}= \frac{(x^2+1)[2x,2y,2z]-(x^2+y^2+z^2)[2x,0,0]}{(x^2+1)^2}, \] which is the same as what we obtained directly.
Chain Rule
As we mentioned earlier, it is in the differentiation of composite functions that we meet apparently substantial alterations of the formula from one-variable calculus. However, if we use the \({\bf D}\) notation, that is, matrix notation for derivatives, the chain rule for functions of several variables looks similar to the one-variable rule.
Theorem 11 Chain Rule
Le} \(U\subset {\mathbb R}^n\) and \(V \subset {\mathbb R}^m\) be open sets. Let \(g\colon\, U\subset {\mathbb R}^n\rightarrow {\mathbb R}^m\) and \(f\colon\, V \subset {\mathbb R}^m\rightarrow {\mathbb R}^p\) be given functions such that \(g\) maps \(U\) into \(V\), so that \(f \circ g\) is defined. Suppose \(g\) is differentiable at \({\bf x}_0\) and \(f\) is differentiable at \({\bf y}_0=g({\bf x}_0)\). Then \(f \circ g\) is differentiable at \({\bf x}_0\) and \begin{equation*} {\bf D}(f\circ g)({\bf x}_0)={\bf D}\! f({\bf y}_0){\bf D}g({\bf x}_0).\tag{1} \end{equation*}
The right-hand side is the matrix product of \({\bf D} f({\bf y}_0)\) with \({\bf D} g({\bf x}_0)\).
127
We shall now give a proof of the chain rule under the additional assumption that the partial derivatives of f are continuous, building up to the general case by developing two special cases that are themselves important. (The complete proof of Theorem 11 without the additional assumption of continuity is given in the Internet supplement for Chapter 2.)
First Special Case of the Chain Rule
Suppose \({\bf c}\colon\, {\mathbb R}\rightarrow {\mathbb R}^3\) is a differentiable path and \(f\colon\, {\mathbb R}^3\rightarrow {\mathbb R}\). Let \(h(t)=f({\bf c}(t))=f(x(t),y(t),z(t)),\) where \({\bf c}(t)=(x(t),y(t),z(t))\). Then \begin{equation*} \frac{{\it dh}}{{\it dt}}= \frac{\partial f}{\partial x}\frac{{\it dx}}{{\it dt}} +\frac{\partial f}{\partial y}\frac{{\it dy}}{{\it dt}} +\frac{\partial f}{\partial z}\frac{{\it dz}}{{\it dt}}.\tag{2} \end{equation*}
That is, \[ \frac{{\it dh}}{{\it dt}}={\nabla}\! f({\bf c}(t))\,{ \cdot}\,{\bf c}'(t), \] where \({\bf c}'(t)=(x'(t),y'(t),z'(t))\).
This is the special case of Theorem 11 in which we take \({\bf c}=g\) and \(f\) to be real-valued, and \(m=3\). Notice that \[ \nabla \! f({\bf c}(t))\,{ \cdot}\,{\bf c}'(t)={\bf D}\! f({\bf c}(t)) {\bf Dc}(t), \] where the product on the left-hand side is the dot product of vectors, while the product on the right-hand side is matrix multiplication, and where we regard \({\bf D}\! f({\bf c}(t))\) as a row matrix and \({\bf Dc}(t)\) as a column matrix. The vectors \(\nabla \! f({\bf c}(t))\) and \({\bf c}'(t)\) have the same components as their matrix equivalents; the notational change indicates the switch from matrices to vectors.
proof of equation (2)
By definition, \[ \frac{dh}{dt}(t_0)=\mathop {{\rm limit}\ }_{t\rightarrow t_0}\frac{h(t)-h(t_0)}{t-t_0}. \]
Adding and subtracting two terms, we write \begin{eqnarray*} \frac{h(t)-h(t_0)}{t-t_0}&=&\frac{f(x(t),y(t),z(t))-f(x(t_0),y(t_0),z(t_0))}{t-t_0}\\[5pt] &=&\frac{f(x(t),y(t),z(t))-f(x(t_0),y(t),z(t))}{t-t_0}\\[5pt] & & +\frac{f(x(t_0),y(t),z(t))-f(x(t_0),y(t_0),z(t))}{t-t_0}\\[5pt] & &+\frac{f(x(t_0),y(t_0),z(t))-f(x(t_0),y(t_0),z(t_0))}{t-t_0}.\\[-15.8pt] \end{eqnarray*}
Now we invoke the mean-value theorem from one-variable calculus, which states: If \(g\colon\, [a,b]\rightarrow {\mathbb R}\) is continuous and is differentiable on the open interval \((a,b)\), then there is a point \(c\) in \((a,b)\) such that \(g(b)-g(a)=g'(c)(b-a)\). Applying this to \(f\) as a function of \(x\), we can assert that for some \(c\) between \(x\) and \(x_0\), \[ f(x,y,z)-f(x_0,y,z)=\bigg[\frac{\partial f}{\partial x}(c,y,z)\bigg] (x-x_0). \]
128
In this way, we find that \begin{eqnarray*} \frac{h(t)-h(t_0)}{t-t_0}&=&\bigg[\frac{\partial f}{\partial x}(c,y(t),z(t))\bigg] \frac{x(t)-x(t_0)}{t-t_0}+ \bigg[\frac{\partial f}{\partial y}(x(t_0),d,z(t))\bigg] \frac{y(t)-y(t_0)}{t-t_0} \\[6pt] && + \bigg[\frac{\partial f}{\partial z}(x(t_0),y(t_0),e)\bigg] \frac{z(t)-z(t_0)}{t-t_0}, \end{eqnarray*} where \(c,d\), and \(e\) lie between \(x(t)\) and \(x(t_0)\), between \(y(t)\) and \(y(t_0)\), and between \(z(t)\) and \(z(t_0)\), respectively. Taking the limit \(t\rightarrow t_0\), using the continuity of the partials \(\partial f/\partial x, \partial f/\partial y, \partial f/\partial z\), and the fact that \(c,d\), and \(e\) converge to \(x(t_0),y(t_0)\), and \(z(t_0)\), respectively, we obtain formula (2).
Second Special Case of the Chain Rule
Let \(f\colon\, {\mathbb R}^3\rightarrow {\mathbb R}\) and let \(g\colon\, {\mathbb R}^3 \rightarrow {\mathbb R}^3\). Write \[ g(x,y,z)=(u(x,y,z) , v(x,y,z) , w(x,y,z)) \] and define \(h\colon\, {\mathbb R}^3\rightarrow {\mathbb R}\) by setting \[ h(x,y,z)=f(u(x,y,z), v(x,y,z), w(x,y,z)). \]
In this case, the chain rule states that \begin{equation*} \bigg[\begin{array}{ccc} \displaystyle \frac{\partial h}{\partial x} &\displaystyle \frac{\partial h}{\partial y} &\displaystyle \frac{\partial h}{\partial z} \end{array}\bigg] = \bigg[\begin{array}{ccc} \displaystyle \frac{\partial f}{\partial u} &\displaystyle \frac{\partial f}{\partial v} &\displaystyle \frac{\partial f}{\partial w} \end{array}\bigg] \left[ \begin{array}{ccc} \displaystyle \frac{\partial u}{\partial x}&\displaystyle \frac{\partial u}{\partial y}&\displaystyle \frac{\partial u}{\partial z}\\[10pt] \displaystyle \frac{\partial v}{\partial x} &\displaystyle \frac{\partial v}{\partial y}&\displaystyle \frac{\partial v}{\partial z}\\[10pt] \displaystyle \frac{\partial w}{\partial x}&\displaystyle \frac{\partial w}{\partial y}&\displaystyle \frac{\partial w}{\partial z} \end{array}\right]\!.\tag{3} \end{equation*}
In this special case, we have taken \(n=m=3\) and \(p=1\) for concreteness, and \(U={\mathbb R}^3\) and \(V={\mathbb R}^3\) for simplicity, and have written out the matrix product \([{\bf D}\! f({\bf y}_0)][{\bf D}g({\bf x}_0)]\) explicitly (with the arguments \({\bf x}_0\) and \({\bf y}_0\) suppressed in the matrices).
proof of the second special case of the chain rule
By definition, \(\partial h/ \partial x\) is obtained by differentiating \(h\) with respect to \(x\), holding \(y\) and \(z\) fixed. But then \((u(x,y,z),v(x,y,z),w(x,y,z))\) may be regarded as a vector function of the single variable \(x\). The first special case applies to this situation and, after the variables are renamed, gives \begin{equation*} \frac{\partial h}{\partial x}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}+\frac{\partial f}{\partial w}\frac{\partial w}{\partial x}.\tag{3'} \end{equation*}
Similarly, \begin{equation*} \frac{\partial h}{\partial y}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial y}+\frac{\partial f}{\partial w}\frac{\partial w}{\partial y}\tag{3''} \end{equation*} and \begin{equation*} \frac{\partial h}{\partial z}=\frac{\partial f}{\partial u}\frac{\partial u}{\partial z}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial z}+\frac{\partial f}{\partial w}\frac{\partial w}{\partial z}.\tag{3'''} \end{equation*}
129
In actual calculations, at the last step, we usually express \(\frac{\partial f}{\partial u}\), \(\frac{\partial f}{\partial v}\), and \(\frac{\partial f}{\partial w}\) in terms of \(x,y,z\). These equations are exactly what would be obtained by multiplying out the matrices in equation (3).
proof of theorem 11
The general case in equation (1) may be proved in two steps. First, equation (2) is generalized to \(m\) variables; that is, for \(f(x_1,\ldots, x_m)\) and \({\bf c}(t)=(x_1(t),\ldots ,x_m(t))\), we have \[ \frac{{\it dh}}{{\it dt}}= \sum^m_{i=1}\frac{\partial f}{\partial x_i}\frac{dx_i}{{\it dt}}, \] where \(h(t)=f(x_1(t),\ldots ,x_m(t))\). Second, the result obtained in the first step is used to obtain the formula \[ \frac{\partial h_j}{\partial x_i}=\sum^m_{k=1}\frac{\partial f_j}{\partial y_k}\frac{\partial y_k}{\partial x_i}, \] where \(f=(f_1,\ldots, f_p)\) is a vector function of arguments \(y_1,\ldots,y_m; g(x_1,\ldots ,x_n) = (y_1(x_1,\) \(\ldots,\) \(x_n),\ldots ,y_m(x_1,\ldots, x_n));\) and \(h_j(x_1,\ldots ,x_n)=f_j(y_1(x_1,\ldots , x_n),\ldots , y_m (x_1,\ldots, x_n))\). (Using the letter \(y\) for both functions and arguments is an abuse of notation, but it can help us remember the formula.) This formula is equivalent to formula (1) after the matrices are multiplied out.
The pattern of the chain rule will become clear once you have worked some additional examples. For instance, \[ \frac{\partial}{\partial x}f(u(x,y),v(x,y),w(x,y),z(x,y))=\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}+\frac{\partial f}{\partial w}\frac{\partial w}{\partial x}+\frac{\partial f}{\partial z}\frac{\partial z}{\partial x}, \] with a similar formula for \(\partial f/\partial y\).
The chain rule can help us understand the relationship between the geometry of a mapping \(f\colon\, {\mathbb R}^2\rightarrow {\mathbb R}^2\) and the geometry of curves in \({\mathbb R}^2\). (Similar statements may be made about \({\mathbb R}^3\) or, generally, \({\mathbb R}^n\).) If \({\bf c}(t)\) is a path in the plane, then as we saw in Section 2.4, \({\bf c'}(t)\) represents the tangent (or velocity) vector of the path \({\bf c}(t)\), and this tangent (or velocity) vector is thought of as beginning at \({\bf c}(t)\). Now let \({\bf p}(t)=f({\bf c}(t))\), where \(f\colon\, {\mathbb R}^2\rightarrow {\mathbb R}^2\). The path \({\bf p}\) represents the image of the path \({\bf c}(t)\) under the mapping \(f\). The tangent vector to \({\bf p}\) is given by the chain rule:
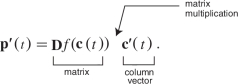
In other words, the derivative matrix of f maps the tangent (or velocity) vector of a path \({\bf c}\) to the tangent (or velocity) vector of the corresponding image path \({\bf p}\) (see Figure 2.49). Thus, points are mapped by f, while tangent vectors to curves are mapped by the derivative of f, evaluated at the base point of the tangent vector in the domain.
130

example 2
Verify the chain rule in the form of formula \((3')\) for \[ f(u,v,w)=u^2+v^2-w, \] where \[ u(x,y,z)=x^2y, v(x,y,z)=y^2, w(x,y,z) =e^{-xz}. \]
solution Here \begin{eqnarray*} h(x,y,z)&=&f(u(x,y,z), v(x,y,z),w(x,y,z))\\[3pt] &=&(x^2y)^2+y^4-e^{-xz}=x^4y^2+y^4-e^{-xz}. \end{eqnarray*}
Thus, differentiating directly, \[ \frac{\partial h}{\partial x}=4x^3y^2+ze^{-xz}. \]
On the other hand, using the chain rule, \begin{eqnarray*} \frac{\partial h}{\partial x}&=&\frac{\partial f}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial f}{\partial v}\frac{\partial v}{\partial x}+\frac{\partial f}{\partial w}\frac{\partial w}{\partial x}=2u(2xy)+2v \,{\cdot}\, 0+(-1)(-ze^{-xz})\\[3pt] &=& (2x^2y)(2xy)+ze^{-xz}, \end{eqnarray*} which is the same as the preceding equation.
example 3
Given \(g(x,y)=(x^2+1,y^2)\) and \(f(u,v)= (u+v,u,v^2),\) compute the derivative of \(f\circ g\) at the point \((x,y)= (1,1)\) using the chain rule.
solution The matrices of partial derivatives are \[ {\bf D}\! f(u,v)=\left[ \begin{array}{c@{\quad}c} \\[-10.5pt] \displaystyle \frac{\partial f_1}{\partial u} &\displaystyle \frac{\partial f_1}{\partial v}\\[10pt] \displaystyle \frac{\partial f_2}{\partial u} &\displaystyle \frac{\partial f_2}{\partial v}\\[10pt] \displaystyle \frac{\partial f_3}{\partial u}&\displaystyle \frac{\partial f_3}{\partial v} \end{array} \right] =\left[ \begin{array}{c@{\quad}c} 1&1\\ 1&0\\ 0&2v \end{array} \right]\!\!\quad\hbox{and}\quad {\bf D}g(x,y)=\bigg[ \begin{array}{c@{\quad}c} 2x&0\\ 0&2y \end{array} \bigg]. \]
131
When \((x,y)=(1,1)\), note that \(g(x,y)=(u,v)=(2,1)\). Hence, \[ {\bf D} (f\circ g)(1,1)={\bf D}\! f(2,1){\bf D}g(1,1)=\left[ \begin{array}{c@{\quad}c} 1&1\\ 1&0\\ 0&2 \end{array} \right] \left[ \begin{array}{c@{\quad}c} 2&0\\ 0&2 \end{array} \right] =\left[ \begin{array}{c@{\quad}c} 2&2\\ 2&0\\ 0&4 \end{array} \right] \] is the required derivative.
example 4
Let \(f(x,y)\) be given and make the substitution \(x=r\cos \theta, y=r\sin \theta\) (polar coordinates). Write a formula for \(\partial f/\partial \theta\).
solution By the chain rule, \[ \frac{\partial f}{\partial \theta}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial \theta}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial \theta}, \] that is, \[ \frac{\partial f}{\partial \theta}=-r \sin \theta \frac{\partial f}{\partial x}+ r\cos \theta \frac{\partial f}{\partial y}. \]
example 5
Let \(f(x,y) = (\cos y +x^2,e^{x+y})\) and \(g(u,v)=(e^{u^2},u-\sin v)\). (a) Write a formula for \(f\circ g\). (b) Calculate \({\bf D} (f\circ g)(0,0)\) using the chain rule.
solution (a) We have \begin{eqnarray*} (f \circ g)(u,v)&=&f(e^{u^2},u-\sin v)\\[2pt] &=& \big(\cos\, (u-\sin v)+e^{2u^2},e^{e^{u^{2}}\,+\,u-\sin v} \big). \end{eqnarray*}
(b) By the chain rule, \[ {\bf D}(f\circ g)(0,0)=[{\bf D}\! f(g(0,0))][{\bf D}g(0,0)]=[{\bf D}\! f(1,0)][{\bf D}g(0,0)]. \]
Now \[ {\bf D}g(0,0)=\left[ \begin{array}{c@{\quad}c} 2ue^{u^2}&0\\ 1&{-}{\cos v} \end{array} \right]_{(u,v)=(0,0)}=\left[\begin{array}{c@{\quad}c} 0&0\\ 1&-1 \end{array} \right] \] and \[ {\bf D}\! f(1,0)=\left[ \begin{array}{c@{\quad}c} 2x&{-}{\sin y}\\ e^{x+y}&e^{x+y} \end{array} \right]_{(x,y)=(1,0)}=\left[\begin{array}{c@{\quad}c} 2&0\\ e&e \end{array} \right]\!. \] [Remember that \({\bf D}\! f\) is evaluated at \(g(0,0)\), not at \((0,0)\)!]. Thus, \[ {\bf D}(f\circ g)(0,0)=\left[ \begin{array}{c@{\quad}c} 2&0\\ e&e \end{array} \right]\left[ \begin{array}{c@{\quad}c} 0&0\\ 1&-1 \end{array} \right]=\left[ \begin{array}{c@{\quad}c} 0&0\\ e&-e \end{array} \right]\!. \]
example 6
Let \(f\colon\, U\subset {\mathbb R}^{n}\rightarrow {\mathbb R}^{m}\) be differentiable, with \(f=(f_1,\ldots ,f_m)\), and let \(g({\bf x})=\sin\,[f({\bf x})\,{ \cdot}\, f{{\bf (x)}}]\). Compute \({\bf D}g({\bf x})\).
132
solution By the chain rule, \({\bf D}g({\bf x})=\cos\, [f({\bf x})\,{ \cdot}\, f({\bf x})]{\bf D}h({\bf x})\), where \(h({\bf x})= [f({\bf x})\,{\cdot}\, f({\bf x})]=f^2_1({\bf x})+ \cdots +f^2_m({\bf x})\). Then \begin{eqnarray*} {\bf D}h(x)&=&\bigg[ \frac{\partial h}{\partial x_1} \quad\cdots\quad \frac{\partial h}{\partial x_n}\bigg]\\[4pt] &=&\bigg[2\! f_1\frac{\partial f_1}{\partial x_1}+\cdots +2\! f_m \frac{\partial f_m}{\partial x_1} \quad\cdots\quad 2\! f_1\frac{\partial f_1}{\partial x_n}+ \cdots + 2\! f_m \frac{\partial f_m}{\partial x_n}\bigg], \end{eqnarray*} which can be written \(2f({\bf x}){\bf D}\! f({\bf x})\), where we regard \(f\) as a row matrix, \[ f=[f_1\quad\cdots\quad f_m] \hbox{and} {\bf D}\! f=\left[ \begin{array}{c@{\quad}c@{\quad}c}\\[-10pt] \displaystyle \frac{\partial f_1}{\partial x_1}&\cdots & \displaystyle \frac{\partial f_1}{\partial x_n}\\ \vdots & &\vdots\\ \displaystyle \frac{\partial f_m}{\partial x_1} &\cdots & \displaystyle \frac{\partial f_m}{\partial x_n} \end{array} \right]\!. \]
Thus, \({\bf D}g({\bf x})=2[\cos\,(f({\bf x}) \,{ \cdot}\, f({\bf x}))]f({\bf x}){\bf D}\! f({\bf x})\).