12.2 Acceleration
In Section 12.1 we studied the basic geometry of paths, learning how to sketch curves (the images of paths) and compute tangent lines. We also learned to think of, as the name suggests, a path as the trajectory of a particle and to regard the derivative of the path as its velocity vector. In this section we continue our study of paths, including additional topics, especially acceleration.
Differentiation of Paths
Recall that a path in \({\mathbb R}^n\) is a map \({\bf c}\) of \(\,{\mathbb R}\) or an interval in \({\mathbb R}\) to \({\mathbb R}^n\). If the path is differentiable, its derivative at each time \(t\) is a vector with \(n\) components. Specifically, if \(x_1(t),\ldots ,x_n(t)\) are the component functions of \({\bf c}(t)\), then its derivative \({\bf c}'(t)\) is given by \[ {\bf c}' (t) = (d x_1/{\it dt},\ldots ,dx_n/{\it dt})\qquad\hbox{or by}\qquad {\bf c}' (t) = (x'_1(t),\ldots ,x'_n(t)). \]
218
Recall from Section 12.1 that \({\bf c}'(t)\) is the tangent vector to the path at the point \({\bf c}(t)\). Also recall that if \({\bf c}\) represents the path of a moving particle, then its velocity vector is \[ {\bf v}={\bf c}'(t), \] and its speed is \(s=\|{\bf v}\|\).
The differentiation of paths is facilitated by the following rules.
Differentiation Rules
Let \({\bf b}(t)\) and \({\bf c}(t)\) be differentiable paths in \({\mathbb R}^3\) and \(p(t)\) and \(q(t)\) be differentiable scalar functions: \[ \begin{array}{r@{\quad}l} {\it Sum Rule}\,\colon &{\displaystyle \frac{d}{{\it dt}}}[{\bf b}(t)+{\bf c}(t)] ={\bf b}'(t)+{\bf c}'(t)\\[15pt] {\it Scalar Multiplication Rule}\,\colon &{\displaystyle\frac{d}{{\it dt}}}[p(t){\bf c}(t)]=p'(t){\bf c} (t)+p(t){\bf c}'(t)\\[15pt] {\it Dot Product Rule}\,\colon & {\displaystyle\frac{d}{{\it dt}}}[{\bf b}(t)\,{\cdot}\, {\bf c}(t)]={\bf b}'(t)\,{\cdot}\, {\bf c}(t)+ {\bf b}(t)\,{\cdot}\,{\bf c}'(t)\\[15pt] {\it Cross Product Rule}\,\colon &{\displaystyle\frac{d}{{\it dt}}}[{\bf b}(t)\times {\bf c}(t)]={\bf b}'(t)\times {\bf c}(t)+{\bf b}(t)\times {\bf c}'(t) \\[15pt] {\it Chain Rule}\,\colon &{\displaystyle\frac{d}{{\it dt}}}[{\bf c}(q(t))]=q'(t){\bf c}'(q(t)) \end{array} \]
These rules follow by applying the usual differentiation rules to the components.
example 1
Show that if \({\bf c}(t)\) is a vector function such that \(\|{\bf c}(t)\|\) is constant, then \({\bf c}'(t)\) is perpendicular to \({\bf c}(t)\) for all \(t\).
solution Because \(\|{\bf c}(t)\|\) is constant, so is its square \(\|{\bf c}(t)\|^2 = {\bf c}(t)\,{\cdot}\, {\bf c}(t)\). The derivative of this constant is zero, so by the dot product rule, \[ 0=\frac{d}{{\it dt}}[{\bf c}(t)\,{\cdot}\, {\bf c}(t)]={\bf c}'(t)\,{\cdot}\, {\bf c}(t)+{\bf c}(t) \,{\cdot}\,{\bf c}'(t)=2{\bf c}(t)\,{\cdot}\, {\bf c}'(t); \] thus, \({\bf c}(t)\,{\cdot}\, {\bf c}'(t)=0\); that is, \({\bf c}'(t)\) is perpendicular to \({\bf c}(t)\).
For a path describing uniform rectilinear motion, the velocity vector is constant. In general, the velocity vector is a vector function \({\bf v}={\bf c}'(t)\) that depends on \(t\). The derivative \({\bf a}=d{\bf v}/{\it dt}={\bf c}''(t)\), if it exists, is called the acceleration of the curve. If the curve is \((x(t),y(t),z(t))\), then the acceleration at time \(t\) is given by \[ {\bf a}(t)=x''(t){\bf i}+y''(t){\bf j}+z''(t){\bf k} \]
example 2
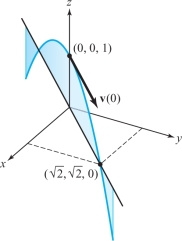
A particle moves in such a way that its acceleration is constantly equal to \(-{\bf k}\). If the position when \(t=0\) is (0, 0, 1) and the velocity at \(t=0\) is \({\bf i}+{\bf j}\), when and where does the particle fall below the plane \(z=0\)? Describe the path traveled by the particle (assume \(t\geq 0\)).
219
solution Let \(\textbf{c}(t)=(x(t),y(t),z(t))=x(t){\bf i}+y(t){\bf j}+z(t){\bf k}\) be the path traced out by the particle, so that the velocity vector is \({\bf c}'(t)=x'(t){\bf i}+y'(t){\bf j}+z'(t){\bf k}\). The acceleration \({\bf c}''(t)\) is \(-{\bf k}\), so \(x''(t)=0,y''(t)=0\), and \(z''(t)=-1\). It follows that \(x'(t)\) and \(y'(t)\) are constant functions, and \(z'(t)\) is a linear function with slope \(-1\). Because \({\bf c}'(0)={\bf i}+{\bf j}\), we get \({\bf c}'(t)={\bf i}+{\bf j}-t{\bf k}\). Integrating again and using the initial position (0, 0, 1), we find that \((x(t),y(t),z(t))= (t,t,1-\frac{1}{2}t^2)\). The particle drops below the plane \(z=0\) when \(1-\frac{1}{2}t^2=0;\) that is, \(t=\sqrt{2}\) (because \(t\ge 0\)). At that instant, the position is \((\sqrt{2},\sqrt{2},0)\). The path traveled by the particle is a parabola in the plane \(y=x\) (see Figure 12.17), because in this plane the equation is described by \(z=1-\frac{1}{2}x^2\).
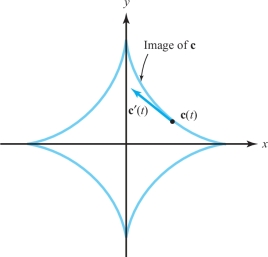
The image of a differentiable path, even one whose derivative is continuous, is not necessarily “very smooth”; indeed, it may have sharp bends or changes of direction. For instance, the cycloid \({\bf c}(t) = ( t - \sin t, 1- \cos t)\) shown in Figure 12.6 in Section 12.1 has cusps at all points where \({\bf c}\) touches the \(x\) axis (that is, when \(1-\cos t=0\), which happens when \(t=2\pi n,n=0,\pm 1,\ldots\)). Another example is the hypocycloid of four cusps, \({\bf c}\colon [0,2\pi]\rightarrow {\mathbb R}^2,t\mapsto (\,\cos^3 t,\,\sin^3 t)\), which has cusps at four points (Figure 12.18). At all such points, however, \({\bf c}'(t)={\bf 0}\), and the tangent line is not well defined. Evidently, the direction of \({\bf c}'(t)\) may change abruptly at points where it slows to rest.
A differentiable path \({\bf c}\) is said to be regular at \(t=t_{0}\) if \({\bf c}'(t_{0}) \ne {\bf 0}\). If \({\bf c}' (t) \ne {\bf 0}\) for all \(t\), we say that \({\bf c}\) is a regular path. In this case, the image curve looks smooth.
example 3
A particle moves along a hypocycloid according to the equations \[ x = \,\cos^3 t , \qquad y = \,\sin^3 t, \qquad a \le t \le b. \]
What are the velocity and speed of the particle?
solution The velocity vector of the particle is \[ {\bf v} = \frac{d x}{{\it dt}} {\bf i} + \frac{d y}{{\it dt}} {\bf j} = - ( 3 \,\sin t \,\cos^2 t) {\bf i} + ( 3 \,\cos t \,\sin^2 t) {\bf j}, \] and its speed is \[ s = \|{\bf v}\| = ( 9 \,\sin^2 t \,\cos^4 t + 9 \,\cos^2 t \,\sin^4 t)^{1/2} = 3\, |\sin t|\ \, |\!\cos t|. \]
Question 12.29 Section 12.2 Progress Check Question 3
A particle moves along a helix as given by the path \({\bf c}(t) = (\cos (4t), \sin (4t), 3t)\). Find the speed of the particle at time \(t=0\).
| A. |
| B. |
| C. |
| D. |
| E. |