Review Exercises from the old Chapter 2
144
Question 13.186
Describe the graphs of:
- (a) \(f (x,y) = 3x^2 + y^2\)
- (b) \(f (x,y) = xy + 3x\)
Question 13.187
Describe some appropriate level surfaces and sections of the graphs of:
- (a) \(f (x,y,z) = 2x^2 + y^2 + z^2\)
- (b) \(f (x,y,z) = x^2\)
- (c) \(f (x,y,z) = xyz\)
Question 13.188
Compute the derivative \({\bf D} f ({\bf x})\) of each of the following functions:
- (a) \(f (x,y) = (x^2 y, e^{-xy})\)
- (b) \(f (x) = (x,x)\)
- (c) \(f (x,y,z) = e^x + e^y + e^z\)
- (d) \(f (x,y,z) = (x,y,z)\)
Question 13.189
Suppose \(f (x,y) = f(y,x)\) for all \((x,y)\). Prove that \[ ( \partial f / \partial x) (a,b)= ( \partial f / \partial y) (b,a). \]
Question 13.190
Let \(f(u, v)=(\cos u, v+\sin u)\) and \(g(x, y, z)=(x^2+\pi y^2, xz)\). Compute \(D(f \circ g)\) at (0, 1, 1) using the chain rule.
Question 13.191
Use the chain rule to find \(D(f \circ g)(-2, 1)\) for \(f(u, v, w)=(v^2+uw, u^2+w^2, u^2v-w^3)\) and \(g(x, y)=(xy^3, x^2-y^2, 3x+5y)\).
Question 13.192
Use the chain rule to find \(D(f \circ g)(-1, 2)\) for \(f(u, v, w)=(v^2+w^2, u^3-vw, u^2v+w)\) and \(g(x, y)=(3x+2y, x^3y, y^2-x^2)\).
Question 13.193
Let \(f(x, y)=(xy, \frac{x}{y}, x+y)\) and \(g(w, s, t)=(we^s, se^{wt})\). Find \(D(f \circ g)(3, 1, 0)\).
Question 13.194
Let \(\textbf{r}(t)=(t\cos(\pi t), t\sin(\pi t), t)\) be a path. Where will the tangent line to \(\textbf{r}\) at \(t=5\) intersect the \(xy\) plane?
Question 13.195
Let \(f(x, y)=x^2e^{-xy}\).
- (a) Find a vector normal to the graph of \(f\) at (1, 2).
- (b) Find the equation of the tangent plane to the graph of \(f\) at (1, 2).
- (c) What point on the surface given by \(z=x^2-y^2\) has a tangent plane parallel to the plane found in (b)?
Question 13.196
Let \(f(x,y) = (1- x^2 - y^2)^{1/2}\). Show that the plane tangent to the graph of \(f\) at \((x_0, y_0, f (x_0, y_0))\) is orthogonal to the vector \((x_0, y_0 ,f (x_0, y_0))\). Interpret geometrically.
Question 13.197
Let \(F(u,v)\) and \(u=h(x,y,z)\), \(v=k(x,y,z)\) be given (differentiable) real-valued functions and let \(f(x,y,z)\) be defined by \(f(x,y,z)=F(h(x,y,z)\), \(k(x,y,z))\). Write a formula for the gradient of \(f\) in terms of the partial derivatives of \(F, h\), and \(k\).
Question 13.198
Find an equation for the tangent plane of the graph of \(f\) at the point \((x_0, y_0, f (x_0, y_0))\) for:
- (a) \(f\colon\, {\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto x - y +2, (x_0, y_0) = (1,1)\)
- (b) \(f\colon\, {\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto x^2 + 4 y^2, (x_0, y_0) = (2,-1)\)
- (c) \(f\colon\, {\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto xy, (x_0, y_0) = (-1,-1)\)
- (d) \(f (x,y) =\, \log\, (x+y)+ x \cos y + \arctan (x+y), (x_0, y_0) = (1,0)\)
- (e) \(f (x,y) = \sqrt{x^2 + y^2},\qquad (x_0, y_0) = (1,1)\)
- (f) \(f (x,y) = xy,\qquad (x_0, y_0) = (2,1)\)
Question 13.199
Compute an equation for the tangent planes of the following surfaces at the indicated points.
- (a) \(x^2 + y^2 + z^2 =3, \qquad\quad (1,1,1)\)
- (b) \(x^3 - 2 y^3 + z^3 =0, \qquad (1,1,1)\)
- (c) \((\cos x) ( \cos y) e^z =0, (\pi /2, 1,0)\)
- (d) \(e^{xyz} =1, (1,1,0)\)
Question 13.200
Draw some level curves for the following functions:
- (a) \(f(x,y) = 1 /xy\)
- (b) \(f(x,y) = x^2 - xy - y^2\)
Question 13.201
Consider a temperature function \(T (x,y)= x \sin y\). Plot a few level curves. Compute \(\nabla T\) and explain its meaning.
Question 13.202
Find the following limits if they exist:
- (a) \({\rm limit}_{(x,y) \to (0,0)} \frac{\cos xy-1}{x}\)
- (b) \({\rm limit}_{(x,y)\to (0,0)}\sqrt{|(x+y) / (x-y)|}, x \ne y\)
Question 13.203
Compute the first partial derivatives and gradients of the following functions:
- (a) \(f(x,y,z) = xe^z + y \cos x\)
- (b) \(f (x,y,z) = (x+ y + z)^{10}\)
- (c) \(f (x,y,z) = (x^2 + y) /z\)
Question 13.204
Compute \(\displaystyle\frac{\partial}{\partial x}[x\exp\,(1+x^2+y^2)]\)
145
Question 13.205
Let \(f \colon \mathbb{R}^2 \to \mathbb{R}^4\) and \(g \colon \mathbb{R}^2 \to \mathbb{R}^2\) be given by \(f(x, z)=(x^2-y^2, 0, \sin(xy), 1)\) and \(g(x, y)=(ye^{x^2}, xe^{y^2})\). Compute \(D(f \circ g)(1, 2)\).
Question 13.206
Let \(f(x, y)=(x^2+y^2)e^{-(x^2+y^2+10)}\). Find the rate of change of \(f\) at (2, 1) in the direction pointing toward the origin.
Question 13.207
Let \(y (x)\) be a differentiable function defined implicitly by \(F (x,y(x)) =0\). From Exercise 19(a), Section 13.4, we know that \[ \frac{dy}{dx} = - \frac{ \partial F / \partial x}{ \partial F/ \partial y}. \]
Consider the surface \(z = F (x,y)\), and suppose \(F\) is increasing as a function of \(x\) and as a function of \(y\); that is, \(\partial F/ \partial x > 0\) and \(\partial F / \partial y > 0\). By considering the graph and the plane \(z=0\), show that for \(z\) fixed at \(z=0\), \(y\) should decrease as \(x\) increases and \(x\) should decrease as \(y\) increases. Does this agree with the minus sign in the formula for \(dy/dx\)?
Question 13.208
Consider the graph of a function \(f (x,y)\) [Figure 13.53]. Let \((x_0, y_0)\) lie on a level curve \(C\), so \(\nabla f (x_0, y_0)\) is perpendicular to this curve. Show that the tangent plane of the graph is the plane that (i) contains the line perpendicular to \(\nabla f (x_0, y_0)\) and lying in the horizontal plane \(z = f (x_0, y_0)\), and (ii) has slope \( \| \nabla f (x_0, y_0) \|\) relative to the \(xy\) plane.
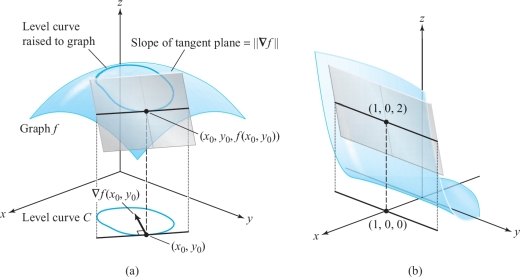 Figure 13.53: (a) The relationship between the gradient of a function and the tangent plane to the graph [Exercise 23(a)]. For a specific instance of the tangent plane in (b) see Exercise 23(b).
Figure 13.53: (a) The relationship between the gradient of a function and the tangent plane to the graph [Exercise 23(a)]. For a specific instance of the tangent plane in (b) see Exercise 23(b).(By the slope of a plane \(P\) relative to the \(xy\) plane we mean the tangent of the angle \(\theta, 0 \le \theta \le \pi\), between the upward-pointing normal \({\bf p}\) to \(P\) and the unit vector \({\bf k}\).)
- Use this method to show that the tangent plane of the graph of \(f (x,y) = (x + \cos y) x^2\) at \((1, 0, 2)\) is as sketched in Figure 13.53.
Question 13.209
Find the plane tangent to the surface \(z = x^2 + y^2\) at the point \((1, -2,5)\). Explain the geometric significance, for this surface, of the gradient of \(f (x,y) = x^2 + y^2\) (see Exercise 23).
Question 13.210
In which direction is the directional derivative of \(f (x,y) = (x^2 - y^2) / (x^2 + y^2)\) at (1, 1) equal to zero?
Question 13.211
Find the directional derivative of the given function at the given point and in the direction of the given vector.
- (a) \(f(x,y,z) = e^x \cos (yz),\qquad p_0 = (0,0,0), {\bf v}= (2,1,-2)\)
- (b) \(f(x,y,z) = xy + yz + zx,\qquad p_0 = (1,1,2), {\bf v} = (10, -1, 2)\)
Question 13.212
Find the tangent plane and normal to the hyperboloid \(x^2 + y^2 - z^2 = 18\) at \((3,5,-4)\).
Question 13.213
Let \((x (t), y(t))\) be a path in the plane, \(0 \le t \le 1\), and let \(f(x,y)\) be a \(C^1\) function of two variables. Assume that \((dx/dt)f_x+(dy/dt)f_y \le 0\). Show that \(f (x (1), y (1)) \le f (x (0), y(0))\).
146
Question 13.214
A bug finds itself in a toxic environment. The toxicity level is given by \(T (x,y) = 2x^2 - 4y^2\). The bug is at \((-1,2)\). In what direction should it move to lower the toxicity the fastest?
Question 13.215
Find the direction in which the function \(w = x^2 + xy\) increases most rapidly at the point \((-1,1)\). What is the magnitude of \(\nabla w\) at this point? Interpret this magnitude geometrically.
Question 13.216
Let \(f\) be defined on an open set \(S\) in \({\mathbb R}^n\). We say that \(f\) is homogeneous of degree \(p\) over \(S\) if \(f ( \lambda {\bf x})= \lambda^p f({\bf x})\) for every real \(\lambda\) and for every \({\bf x}\) in \(S\) for which \(\lambda {\bf x} \in S\).
- (a) If such a function is differentiable at \({\bf x}\), show that \({\bf x}\,{ \cdot}\, \nabla f ({\bf x})= pf ( {\bf x})\). This is known as Euler’s theorem for homogeneous functions. [HINT: For fixed x, define \(g ( \lambda)= f ( \lambda {\bf x})\) and compute \(g'(1)\).]
- (b) Find \(p\) and check Euler’s theorem for the function \(f (x,y,z) = x- 2y - \sqrt{xz},\) on the region where \(xz > 0\).
Question 13.217
If \(z= [ f(x-y) ]/y\) (where \(f\) is differentiable and \(y\neq 0\)), show that the identity \(z + y( \partial z / \partial x) + y ( \partial z / \partial y) =0\) holds.
Question 13.218
Given \(z= f((x +y)/ (x-y))\) for \(f\) a \(C^1\) function, show that \[ x \frac{\partial z}{\partial x} + y \frac{\partial z}{ \partial y} =0. \]
Question 13.219
Let \(f\) have partial derivatives \(\partial f ( {\bf x}) / \partial x_i\), where \(i=1,2, \ldots , n\), at each point \({\bf x}\) of an open set \(U\) in \({\mathbb R}^n\). If \(f\) has a local maximum or a local minimum at the point \({\bf x}_0\) in \(U\), show that \(\partial f ({\bf x}_0) / \partial x_i =0\) for each \(i\).
Question 13.220
Consider the functions defined in \({\mathbb R}^2\) by the following formulas:
- (i) \(f(x,y) = xy / (x^2 + y^2) \quad \hbox{if} \quad (x,y) \ne (0,0), f (0,0) =0\)
- (ii) \(f(x,y) = x^2y^2 / (x^2 + y^4) \quad \hbox{if} \quad (x,y) \ne (0,0), f (0,0) =0\)
- (a) In each case, show that the partial derivatives \(\partial f (x,y)/ \partial x\) and \(\partial f (x,y)/ \partial y\) exist for every \((x,y)\) in \({\mathbb R}^2\), and evaluate these derivatives explicitly in terms of \(x\) and \(y\).
- (b) Explain why the functions described in (i) and (ii) are or are not differentiable at (0, 0).
Question 13.221
Compute the gradient vector \(\nabla f(x,y)\) at all points \((x,y)\) in \({\mathbb R}^2\) for each of the following functions:
- (a) \(f(x,y) = x^2 y^2 \log\, ( x^2 + y^2 ) \quad \hbox{if} (x,y) \ne (0,0), f (0,0) =0\)
- (b) \(f(x,y) = x y \sin\, [1 / (x^2 + y^2 )] \quad \hbox{if} (x,y) \ne (0,0), \qquad f (0,0) =0\)
Question 13.222
Find the directional derivatives of the following functions at the point \((1, 1)\) in the direction \(({\bf i} + {\bf j})/ \sqrt{2}\):
- (a) \(f(x,y) = x \tan^{-1}\, (x/y)\)
- (b) \(f(x,y) = \cos\, (\sqrt{x^2 + y^2})\)
- (c) \(f(x,y) = \exp\, (-x^2 - y^2)\)
Question 13.223
- (a) Let \({\bf u} = {\bf i} - 2 {\bf j} +2 {\bf k}\) and \({\bf v} = 2 {\bf i} + {\bf j} - 3 {\bf k}\). Find: \(\| {\bf u} \| , {\bf u}\,{ \cdot}\,{\bf v},{\bf u} \times {\bf v}\), and a vector in the same direction as \({\bf u}\), but of unit length.
- (b) Find the rate of change of \(e^{xy} \sin (xyz)\) in the direction \({\bf u}\) at \((0, 1, 1)\).
Question 13.224
Let \(h (x,y) = 2 e^{-x^2} + e^{-3y^2}\) denote the height on a mountain at position \((x,y)\). In what direction from \((1, 0)\) should one begin walking in order to climb the fastest?
Question 13.225
Compute an equation for the plane tangent to the graph of \[ f(x,y) = \frac{e^x}{x^2 + y^2} \] at \(x=1, y=2\).
Question 13.226
- (a) Give a careful statement of the general form of the chain rule.
- (b) Let \(f(x,y) = x^2 + y\) and \({\bf h} (u)= ( \sin 3u, \cos 8u)\). Let \(g(u) = f({\bf h} (u))\). Compute \(dg/du\) at \(u=0\) both directly and by using the chain rule.
Question 13.227
- (a) Sketch the level curves of \(f(x,y) = - x^2 - 9 y^2\) for \(c=0, -1,-10.\)
- (b) On your sketch, draw in \(\nabla f\) at \((1,1)\). Discuss.
Question 13.228
At time \(t=0\), a particle is ejected from the surface \(x^2 + 2 y^2 + 3 z^2 =6\) at the point \((1, 1, 1)\) in a direction normal to the surface at a speed of 10 units per second. At what time does it cross the sphere \(x^2 + y^2 + z^2 =103\)?
Question 13.229
At what point(s) on the surface in Exercise 43 is the normal vector parallel to the line \(x=y=z\)?
Question 13.230
Compute \(\partial z / \partial x\) and \(\partial z / \partial y\) if \[ z = \frac{u^2 + v^2}{u^2 - v^2}, \qquad u = {\mathop e}^{-x-y}, \qquad v = e^{xy} \] (a) by substitution and direct calculation, and (b) by the chain rule.
147
Question 13.231
Compute the partial derivatives as in Exercise 45 if \(z= uv, u = x+y,\) and \(v=x-y\).
Question 13.232
What is wrong with the following argument? Suppose that \(w = f(x,y)\) and \(y = x^2\). By the chain rule, \[ \frac{\partial w}{\partial x} = \frac{\partial w}{\partial x} \frac{\partial x}{\partial x} + \frac{\partial w\, \partial y}{\partial y\, \partial x} = \frac{\partial w}{\partial x} + 2x \frac{\partial w}{\partial y} . \]
Hence, \(0 = 2x ( \partial w/ \partial y)\), and so \(\partial w / \partial y =0\). Choose an explicit example to really see that this is incorrect.
Question 13.233
A boat is sailing northeast at 20 km/h. Assuming that the temperature drops at a rate of 0.2\(^\circ\)C/km in the northerly direction and 0.3\(^\circ\)C/km in the easterly direction, what is the time rate of change of temperature as observed on the boat?
Question 13.234
Use the chain rule to find a formula for \((d /dt) \,{\exp}\, [f(t) g(t)].\)
Question 13.235
Use the chain rule to find a formula for \((d/ dt) ( f (t)^{g(t)})\).
Question 13.236
Verify the chain rule for the function \(f(x,y,z) = [ \ln\, (1+ x^2 + 2 z^2)] /(1 + y^2)\) and the path \({\bf c} (t) = (t, 1- t^2, \cos t)\).
Question 13.237
Verify the chain rule for the function \(f(x,y) = x^2 / (2 + \cos y)\) and the path \(x = e^t,\) \(y= e^{-t}\).
Question 13.238
Suppose that \(u (x,t)\) satisfies the differential equation \(u_t + uu_x =0\) and that \(x\), as a function \(x= f(t)\) of \(t\), satisfies \(dx/dt = u(x,t)\). Prove that \(u ( f(t),t)\) is constant in \(t\).
Question 13.239
The displacement at time \(t\) and horizontal position on a line \(x\) of a certain violin string is given by \(u = \sin\, ( x- 6t) + \sin\, ( x+ 6t)\). Calculate the velocity of the string at \(x=1\) when \(t = \frac{1}{3}\).
Question 13.240
The ideal gas law \(PV = nRT\) involves a constant \(R\), the number \(n\) of moles of the gas, the volume \(V\), the Kelvin temperature \(T\), and the pressure \(P\).
- (a) Show that each of \(n,P,T,V\) is a function of the remaining variables, and determine explicitly the defining equations.
- (b) Calculate \(\partial V / \partial T, \partial T / \partial P, \partial P / \partial V\) and show that their product equals \(-1\).
Question 13.241
The potential temperature \(\theta\) is defined in terms of temperature \(T\) and pressure \(p\) by \[ \theta = T \left( \frac{1000}{p} \right)^{0.286}. \]
The temperature and pressure may be thought of as functions of position \((x,y,z)\) in the atmosphere and also of time \(t\).
- (a) Find formulas for \(\partial \theta / \partial x, \partial \theta / \partial y, \partial \theta / \partial z, \partial \theta / \partial t\) in terms of partial derivatives of \(T\) and \(p\).
- (b) The condition \(\partial \theta / \partial z < 0\) is regarded as an unstable atmosphere, for it leads to large vertical excursions of air parcels from a single upward or downward impetus. Meteorologists use the formula \[ \frac{\partial \theta}{\partial z}= \frac{\theta}{T} \left( \frac{\partial T}{\partial z} + \frac{g}{C_p} \right), \] where \(g=32.2\) and \(C_p\) is a positive constant. How does the temperature change in the upward direction for an unstable atmosphere?
Question 13.242
The specific volume \(V\), pressure \(P\), and temperature \(T\) of a van der Waals gas are related by \(P = RT / ( V- \beta ) - \alpha / V^2\), where \(\alpha, \beta,\) and \(R\) are constants.
- (a) Explain why any two of \(V,P\), and \(T\) can be considered independent variables that determine the third variable.
- (b) Find \(\partial T / \partial P, \partial P / \partial V, \partial V / \partial T\). Identify which variables are constant, and interpret each partial derivative physically.
- (c) Verify that \(( \partial T / \partial P) ( \partial P / \partial V) ( \partial V / \partial T) = -1 (\hbox{ not } +\! 1!)\).
Question 13.243
The height \(h\) of the Hawaiian volcano Mauna Loa is (roughly) described by the function \(h (x,y) = 2.59 - 0.00024y^2 - 0.00065 x^2\), where \(h\) is the height above sea level in miles and \(x\) and \(y\) measure east–west and north–south distances in miles from the top of the mountain. At \((x,y) = (-2, -4)\):
- (a) How fast is the height increasing in the direction \((1, 1)\) (that is, northeastward)? Express your answer in miles of height per mile of horizontal distance traveled.
- (b) In what direction is the steepest upward path?
Question 13.244
- (a) In what direction is the directional derivative of \(f(x,y) = ( x^2 - y^2)/ (x^2 + y^2)\) at (1, 1) equal to zero?
- (b) How about at an arbitrary point \((x_0, y_0)\) in the first quadrant?
- (c) Describe the level curves of \(f\). In particular, discuss them in terms of the result of part (b).
148
Question 13.245
- (a) Show that the curve \(x^2 -y^2=c\), for any value of \(c\), satisfies the differential equation \(dy/dx = x/y\).
- (b) Draw in a few of the curves \(x^2 - y^2=c\), say for \(c= \pm 1\). At several points \((x,y)\) along each of these curves, draw a short segment of slope \(x/y\); check that these segments appear to be tangent to the curve. What happens when \(y=0\)? What happens when \(c=0\)?
Question 13.246
Suppose that \(f\) is a differentiable function of one variable and that a function \(u = g (x,y)\) is defined by \[ u = g (x,y)= xyf \left( \frac{x+y}{xy} \right). \]
Show that \(u\) satisfies a (partial) differential equation of the form \[ x^2 \frac{ \partial u}{ \partial x} - y^2 \frac{\partial u}{ \partial y}= G (x,y) u \] and find the function \(G (x,y)\).
Question 13.247
- (a) Let \(F\) be a function of one variable and \(f\) a function of two variables. Show that the gradient vector of \(g (x,y) = F (f (x,y))\) is parallel to the gradient vector of \(f(x,y)\).
- (b) Let \(f(x,y)\) and \(g(x,y)\) be functions such that \(\nabla f = \lambda \nabla g\) for some function \(\lambda (x,y)\). What is the relation between the level curves of \(f\) and \(g\)? Explain why there might be a function \(F\) such that \(g (x,y) = F(f(x,y))\).
1Some mathematicians would write such an \(f\) in boldface, using the notation \({\bf f}({\bf x})\), because the function is vector-valued. We did not do so, as a matter of personal taste. We use boldface primarily for mappings that are vector fields, introduced later. The notion of function was developed over many centuries, with the definition extended to cover more cases as they arose. For example, in 1667 James Gregory defined a function as “a quantity obtained from other quantities by a succession of algebraic operations or by any other operation imaginable.” In 1755 Euler gave the following definition: “If some quantities depend on others in such a way as to undergo variation when the latter are varied then the former are called functions of the latter.”
2It turns out that we need to postulate the existence of only some matrix giving the best linear approximation near \({\bf x}_0\in {\mathbb R}^n\), because in fact this matrix is necessarily the matrix whose \(ij\)th entry is \(\partial f_i/\partial x_j\) (see the Internet supplement for Chapter 2).
3If \(t\) lies at the endpoint of an interval, we should, as in one-variable calculus, take right- or left-handed limits.
4See S. M. Binder, “Mathematical Methods in Elementary Thermodynamics,” J. Chem. Educ., 43 (1966): 85–92. A proper understanding of partial differentiation can be of significant use in applications; for example, see M. Feinberg, “Constitutive Equation for Ideal Gas Mixtures and Ideal Solutions as Consequences of Simple Postulates,” Chem. Eng. Sci., 32 (1977): 75–78.
5This discussion assumes that one walks at the same speed in all directions. Of course, hikers know that this is not necessarily realistic.