Question 13.280

\({\bf V}(x,y,z)=e^{xy}{\bf i}-e^{xy}{\bf j}+e^{yz}{\bf k}\)

Question 13.281

\({\bf V} (x,y,z)=yz{\bf i}+xz{\bf j}+xy{\bf k}\)

Question 13.282

\({\bf V}(x,y,z)=x{\bf i}+(y+\cos x){\bf j}+(z+e^{xy}){\bf k}\)

Question 13.283

\({\bf V}(x,y,z)=x^2{\bf i}+(x+y)^2{\bf j}+(x+y+z)^2{\bf k}\)

Question 13.284

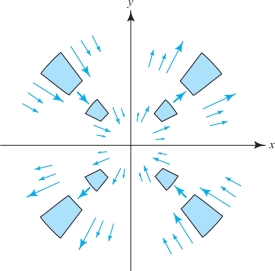
Figure 13.37 shows some flow lines and moving regions for a fluid moving in the plane-field velocity field \({\bf V}\). Where is div \({\bf V} > 0\), and also where is div \({\bf V} < 0\)?

Question 13.285

Let \(V(x,y,z)=x{\bf i}\) be the velocity field of a fluid in space. Relate the sign of the divergence with the rate of change of volume under the flow.

Question 13.286

Sketch a few flow lines for \({\bf F}(x,y)=y{\bf i}\). Calculate \(\nabla\,{\cdot}\, {\bf F}\) and explain why your answer is consistent with your sketch.

Question 13.287

Sketch a few flow lines for \({\bf F}(x,y)=-3x{\bf i}-y{\bf j}\). Calculate \(\nabla \,{\cdot}\, {\bf F}\) and explain why your answer is consistent with your sketch.

Question 13.288

\({\bf F}(x,y)=x^3{\bf i}-x\sin\, (xy){\bf j}\)

Question 13.289

\({\bf F}(x,y)=y{\bf i}-x{\bf j}\)

Question 13.290

\({\bf F}(x,y)=\sin\, (xy){\bf i} -\cos\, (x^2y){\bf j}\)

Question 13.291

\({\bf F}(x,y)=xe^y{\bf i}-[\,y/(x+y)]{\bf j}\)

Question 13.292

\({\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}\)

Question 13.293

\({\bf F}(x,y,z)=yz{\bf i}+xz{\bf j}+xy{\bf k}\)

Question 13.294

\({\bf F}(x,y,z)=(x^2+y^2+z^2)(3{\bf i}+4{\bf j}+5{\bf k})\)

Question 13.295

\({\bf F}(x,y,z)=\displaystyle\frac{yz{\bf i}-xz{\bf j}+xy{\bf k}}{x^2+y^2+z^2}\)

Question 13.296

\({\bf F}(x,y)=\sin x{\bf i}+\cos x{\bf j}\)

Question 13.297

\({\bf F}(x,y)=y{\bf i}-x{\bf j}\)

Question 13.298

\({\bf F}(x,y)=xy{\bf i}+(x^2-y^2){\bf j}\)

Question 13.299

\({\bf F}(x,y)=x{\bf i}+y{\bf j}\)

Question 13.300

Let \(\textbf{F}(x,y,z)=(x^2,x^2y,z+zx)\).

• (a) Verify that \(\nabla \cdot (\nabla \times \textbf{F}) =0\).
• (b) Can there exist a function \(f \colon \mathbb R^3 \to \mathbb R\) such that \(\textbf{F}=\nabla f\)? Explain.

Question 13.301

• (a) Which of the vector fields in Exercises 13–16 could be gradient fields?
• (b) Which of the vector fields in Exercises 9–12 could be the curl of some vector field \(\textbf{V} \colon \mathbb R^3 \to \mathbb R^3\)?

Question 13.302

Let \(\textbf{F}(x, y, z)=(e^{xz}, \sin(xy), x^5y^3z^2)\).

• (a) Find the divergence of \(\textbf{F}\).
• (b) Find the curl of \(\textbf{F}\).

Question 13.303

Suppose \(f\colon \mathbb R^3 \to \mathbb R\) is a \(C^2\) scalar function. Which of the following expressions are meaningful, and which are nonsense? For those which are meaningful, decide whether the expression defines a scalar function or a vector field.

• (a) curl(grad\(f\))
• (b) grad(curl \(f\)))
• (c) div(grad \(f\))
• (d) grad(div \(f\))
• (e) curl (div \(f\))
• (f) div(curl \(f\))

Question 13.304

Suppose \(\textbf{F}\colon \mathbb R^3 \to \mathbb R^3\) is a \(C^2\) vector field. Which of the following expressions are meaningful, and which are nonsense? For those which are meaningful, decide whether the expression defines a scalar function or a vector field.

• (a) curl(grad \(\textbf{F}\))
• (b) grad(curl \(\textbf{F}\)))
• (c) div(grad \(\textbf{F}\))
• (d) grad(div \(\textbf{F}\))
• (e) curl (div \(\textbf{F}\))
• (f) div(curl \(\textbf{F}\))

Question 13.305

Suppose \(f, g, h \colon \mathbb R \to \mathbb R\) are differentiable. Show that the vector field \(\textbf{F}(x, y, z)= \big( f(x), g(y), h(z) \big)\) is irrotational.

Question 13.306

Suppose \(f, g, h \colon \mathbb R^2 \to \mathbb R\) are differentiable. Show that the vector field \(\textbf{F}(x, y, z)= \big( f(y, z), g(x, z), h(x, y) \big)\) has zero divergence.

Question 13.307

Prove identity 13 in the list of vector identities.

Question 13.308

\(f(x,y,z)=\sqrt{x^2+y^2+z^2}\)

Question 13.309

\(f(x,y,z)=xy+yz+xz\)

Question 13.310

\(f(x,y,z)=1/(x^2+y^2+z^2)\)

Question 13.311

\(f(x,y,z)=x^2y^2+y^2z^2\)

Question 13.312

Show that \({\bf F}=y(\cos x){\bf i}+x(\sin y){\bf j}\) is not a gradient vector field.

Question 13.313

Show that \({\bf F}=(x^2+y^2){\bf i}-2xy{\bf j}\) is not a gradient field.

260

Question 13.314

Prove identity 10 in the list of vector identities.

Question 13.315

Suppose that \(\nabla \,{\cdot}\, {\bf F}= 0\) and \(\nabla \,{\cdot}\, {\bf G}=0\). Which of the following necessarily have zero divergence?

• (a) \({\bf F}+{\bf G}\)
• (b) \({\bf F}\times {\bf G}\)

Question 13.316

Let \({\bf F}=2xz^2{\bf i}+{\bf j}+y^3 zx{\bf k}\) and \(f=x^2y\). Compute the following quantities.

• (a) \(\nabla f\)
• (b) \(\nabla \times {\bf F}\)
• (c) \({\bf F}\times \nabla f\)
• (d) \({\bf F} \,{\cdot}\, (\nabla f)\)

Question 13.317

Let \({\bf r}(x,y,z)=(x,y,z)\) and \(r=\sqrt{x^2+y^2+z^2}=\|{\bf r}\|\). Prove the following identities.

• (a) \(\nabla (1/r)=-{\bf r}/r^3,r\neq 0\); and, in general, \(\nabla (r^n)=nr^{n-2}{\bf r}\) and \(\nabla (\log r)={\bf r}/r^2\).
• (b) \(\nabla^2 (1/r)=0,r\neq 0;\) and, in general, \(\nabla^2 r^n=n(n+1)\,r^{n-2}.\)
• (c) \(\nabla \,{\cdot}\, ({\bf r}/r^3)=0;\) and, in general, \(\nabla \,{\cdot}\, (r^n {\bf r})=(n+3)\,r^n\).
• (d) \(\nabla \times {\bf r} = {\bf 0};\) and, in general, \(\nabla \times (r^n {\bf r})={\bf 0}\).

Question 13.318

Does \(\nabla \times {\bf F}\) have to be perpendicular to \({\bf F}\)?

Question 13.319

Let \({\bf F}(x,y,z)=3 x^2 y{\bf i}+(x^3+y^3){\bf j}\).

• (a) Verify that curl \({\bf F}={\bf 0}\).
• (b) Find a function \(f\) such that \({\bf F}=\nabla f\). (Techniques for constructing \(f\) in general are given in Chapter 8. The one in this problem should be sought by trial and error.)

Question 13.320

Show that the real and imaginary parts of each of the following complex functions form the components of an irrotational and incompressible vector field in the plane; here \(i=\sqrt{-1}.\)

• (a) \((x-iy)^2\)
• (b) \((x-iy)^3\)
• (c) \(e^{x-iy}=e^x(\cos y-i\sin y)\)