13.8 Newton’s Second Law
220
If a particle of mass \(m\) moves in \({\mathbb R}^3\), the force vector field \({\bf F}\) acting on it at the point \({\bf c}(t)\) is related to the acceleration \({\bf a}(t)\) by Newton’s second law: \[ {\bf F} \hbox{(}{\bf c}\hbox{(}t\hbox{)}\hbox{)} = m {\bf a}\hbox{(}t\hbox{)}. \]
In particular, if no forces act on a particle, then \({\bf a}(t)={\bf 0}\), so \({\bf c}'(t)\) is constant and the particle follows a straight line.
Acceleration and Newton’s Second Law
The acceleration of a twice differentiable path \({\bf c}(t)\) is \[ {\bf a}(t)={\bf c}''(t). \]
If \({\bf F}\) is the force acting and \(m\) is the mass of the particle, then \[ {\bf F}=m{\bf a}. \]
In the problem of determining the path \({\bf c}(t)\) of a particle under the influence of a given force field, \({\bf F}\), Newton’s law becomes a differential equation (i.e., an equation involving derivatives) for \({\bf c}(t)\).
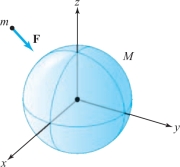
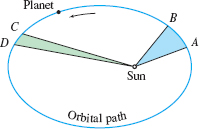
For example, the motion of a planet moving along a path \({\bf r}(t)\) around the sun (considered to be located at the origin in \({\mathbb R}^3\)) obeys the law \[ m{\bf r}''=-\frac{GmM}{r^3}{\bf r}, \] where \(M\) is the mass of the sun, \(m\) that of the planet, \(r=\|{\bf r}\|\), and \(G\) is the gravitational constant. The relation used in determining the force, \({\bf F}=-GmM{\bf r}/r^3\), is called Newton’s law of gravitation (see Figure 13.78). We begin with the special case of circular orbits.
Circular Orbits
Consider a particle of mass \(m\) moving at constant speed \(s\) in a circular path of radius \(r_0\). Supposing that it moves in the \(xy\) plane, we can suppress the third component and write its location as \[ {\bf r} (t) = \bigg( r_0 \cos \big(\frac{st}{r_0}\big), r_0 \sin \big(\frac{st}{r_0}\big) \bigg). \]
221
Note that this is a circle of radius \(r_{0}\) and that its speed is given by \(\|{\bf r}{'} (t)\|=s\). The quantity \(s/r_{0}\) is called the frequency and is denoted \(\omega\). Thus, \[ {\bf r}(t) = (r_{0} \cos \, (\omega t), \ r_{0} \sin \, (\omega t)). \]
The acceleration is given by \[ {\bf a} (t) = {\bf r}'' (t) = \bigg({-} \frac{s^2}{r_0} \cos \big(\frac{s t}{r_0}\big), {-}\frac{s^2}{r_0} \sin \big(\frac{s t}{r_0}\big) \bigg) ={-}\frac{s^2}{r^2_0}{\bf r} (t) =-\omega^2{\bf r}(t). \]
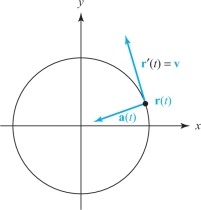
Thus, the acceleration is in a direction opposite to \({\bf r} (t);\) that is, it is directed toward the center of the circle (see Figure 13.79). This acceleration multiplied by the mass of the particle is called the centripetal force. Even though the speed is constant, the direction of the velocity is continuously changing and therefore the acceleration, which is a rate of change in either speed or direction or both, is nonzero.
Newton’s law helps us discover a relationship between the radius of the orbit of a revolving body and the period; that is, the time it takes for one complete revolution. Consider a satellite of mass \(m\) moving with a speed \(s\) around a central body with mass \(M\) in a circular orbit of radius \(r_0\) (distance from the center of the spherical central body). By Newton’s second law \({\bf F}=m{\bf a}\), we get \[ -\frac{s^2 m}{r^2_0}{\bf r}(t)=-\frac{GmM}{r^3_0}{\bf r}(t). \]
The lengths of the vectors on both sides of this equation must be equal. Hence \[ s^2=\frac{{\it GM}}{r_0}. \]
If \(T\) denotes the period, then \(s=2\pi r_0/T\); substituting this value for \(s\) in the preceding equation and solving for \(T\), we obtain the following:
Kepler’s Third Law (Circular Orbits)
\[ T^2=r^3_0\frac{(2\pi)^2}{{\it GM}}. \] Thus, the square of the period is proportional to the cube of the radius.
222
example 1
Suppose that a satellite is to be in a circular orbit about the earth such that it stays fixed in the sky over one point on the equator. What is the radius of such a geosynchronous orbit? (The mass of the earth is \(5.98 \times 10^{24}\) kilograms and \(G=6.67 \times 10^{-11}\) in the meter-kilogram-second [kgs] system of units.)
solution The period of the satellite should be 1 day, so \(T=60\,\times\, 60 \times 24 ={86{,}400}\) seconds. From the formula \(T^2=r^3_0(2\pi)^2/{\it GM}\), we get \(r^3_0=T^2{\it GM}/(2\pi)^2\), and so \[ r^3_0 = \frac{T^2{\it GM}}{(2\pi)^2}=\frac{(86{,}400)^2\times (6.67\times 10^{-11})\times (5.98\times 10^{24})}{(2\pi)^2} \approx 7.54 \times 10^{22}\,{\rm m}^3. \]
Thus, \(r_0=4.23\times 10^7 \,{\rm m} ={42{,}300}\,{\rm km}\approx {26{,}200}\, {\rm mi.}\)
We mow delve more deeply into all of Kepler's laws of Planetary Motion.
Planetary Motion According to Kepler and Newton
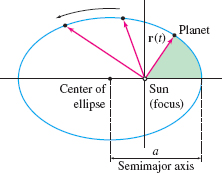
According to Kepler, the planetary orbits are ellipses with the sun at one focus. Furthermore, if we imagine a radial vector \({\bf r}(t)\) pointing from the sun to the planet, as in Figure 13.80, then this radial vector sweeps out area at a constant rate or, as Kepler stated in his Second Law, the radial vector sweeps out equal areas in equal times (Figure 13.81). As we have seen, Kepler’s Third Law determines the period \(T\) of the orbit, defined as the time required to complete one full revolution. These laws are valid not just for planets orbiting the sun, but for any body orbiting about another body according to the inverse-square law of gravitation.
766
- (i) Law of Ellipses: The orbit of a planet is an ellipse with the sun at one focus.
- (ii) Law of Equal Area in Equal Time: The position vector pointing from the sun to the planet sweeps out equal areas in equal times.
- (iii) Law of the Period of Motion: \(\displaystyle{T^2=\left(\frac{4\pi^2}{GM}\right)a^3}\), where
- \(a\) is the semimajor axis of the ellipse (Figure 13.80).
- \(G\) is the universal gravitational constant: \(6.673 \times 10^{-11} \mathrm{m}^3\,\mathrm{kg}^{-1}\,\mathrm{s}^{-2}\)
- \(M\) is the mass of the sun, approximately \(1.989\times 10^{30}\) kg.
Note
Kepler’s version of the Third Law stated only that \(T^2\) is proportional to \(a^3\). Newton discovered that the constant of proportionality is equal to \(4\pi^2/(GM)\), and he observed that if you can measure \(T\) and \(a\) through observation, then you can use the Third Law to solve for the mass \(M\). This method is used by astronomers to find the masses of the planets (by measuring \(T\) and \(a\) for moons revolving around the planet) as well as the masses of binary stars and galaxies. See Exercises 2-5.
Our derivation makes a few simplifying assumptions. We treat the sun and planet as point masses and ignore the gravitational attraction of the planets on each other. And although both the sun and the planet revolve around their mutual center of mass, we ignore the sun’s motion and assume that the planet revolves around the center of the sun. This is justified because the sun is much more massive than the planet.
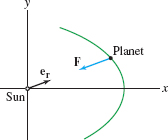
We place the sun at the origin of the coordinate system. Let \({\bf r} = {\bf r}(t)\) be the position vector of a planet of mass \(m\), as in Figure 13.80, and let (Figure 13.82) \[ {\bf e}_r = \frac{{\bf r}(t)}{\|{\bf r}(t)\|} \] be the unit radial vector at time \(t\) (\({\bf e}_r\) is the unit vector that points to the planet as it moves around the sun).
By Newton’s Universal Law of Gravitation (the inverse-square law)\index{Universal Law of Gravitation}, the sun attracts the planet with a gravitational force \[ {\bf F}({\bf r}(t))= -\left(\frac{km}{\|{\bf r}(t)\|^2} \right){\bf e}_r \] where \(k=GM\) (Figure 13.82). Combining the Law of Gravitation with Newton’s Second Law of Motion \({\bf F}({\bf r}(t)) = m{\bf r}''(t)\), we obtain \[ \boxed{\bbox[#FAF8ED,5pt]{ {\bf r}''(t) = - \frac{k}{\|{\bf r}(t)\|^2}\, {\bf e}_r}}\tag{1} \]
Kepler’s Laws are a consequence of this differential equation.
Kepler’s Second Law
The key to Kepler’s Second Law is the fact that the following cross product is a constant vector (even though both \({\bf r}(t)\) and \({\bf r}'(t)\) are changing in time): \[ \boxed{\bbox[#FAF8ED,5pt]{{\bf J} = {\bf r}(t)\times {\bf r}'(t)}} \]
THEOREM 1
The vector \({\bf J}\) is constant—that is, \[ \boxed{\bbox[#FAF8ED,5pt]{\dfrac{d{\bf J}}{dt} = \mathbf{0}}}\tag{2} \]
Note
In physics, \(m{\bf J}\) is called the angular momentum vector. In situations where \({\bf J}\) is constant, we say that angular momentum is conserved. This conservation law is valid whenever the force acts in the radial direction.
767
Proof
By the Product Rule for cross products (Theorem 3 in Section 13.2) \[ \frac{d{\bf J}}{dt} = \frac{d}{dt} \bigl({\bf r}(t)\times{\bf r}'(t)\bigr) = {\bf r}(t)\times {\bf r}''(t) + {\bf r}'(t)\times {\bf r}'(t) \]
The cross product of parallel vectors is zero, so the second term is certainly zero. The first term is also zero because \({\bf r}''(t)\) is a multiple of \( {\bf e}_r \) by Eq. (1),and hence also of \({\bf r}(t)\).
REMINDER
- \({\bf a} \times {\bf b}\) is orthogonal to both \({\bf a}\) and \({\bf b}\)
- \({\bf a}\times {\bf b}={\bf 0}\) if \({\bf a}\) and \({\bf b}\) are parallel, that is, one is a multiple of the other.
How can we use Eq. (1)? First of all, the cross product \({\bf J}\) is orthogonal to both \({\bf r}(t)\) and \({\bf r}'(t)\). Because \({\bf J}\) is constant, \({\bf r}(t)\) and \({\bf r}'(t)\) are confined to the fixed plane orthogonal to \({\bf J}\). This proves that the motion of a planet around the sun takes place in a plane
We can choose coordinates so that the sun is at the origin and the planet moves in the counterclockwise direction (Figure 13.83). Let \((r,\theta)\) be the polar coordinates of the planet, where \(r=r(t)\) and \(\theta=\theta(t)\) are functions of time. Note that \(r(t) = \|{\bf r}(t)\|\).
Now the area swept out by the planet’s radial vector is \[ A = \frac12\int_0^\theta\,r^2\,d\theta \]
Note
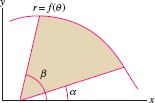
The region bounded by the polar curve \(r=f(\theta)\) and the rays \(\theta=\alpha\), \(\theta=\beta\) has area \(\frac12\int \limits_{\alpha}^{\beta} f(\theta)^2\, d\theta\). This formula from single-variable calculus can be justified with Riemann sums, but for a rigorous proof see Example ?? in Section 16.2.
Kepler’s Second Law states that this area is swept out at a constant rate. But this rate is simply \(\displaystyle{\frac{dA}{dt}}\). By the Fundamental Theorem of Calculus, \(\displaystyle{\frac{dA}{d\theta} = \frac12r^2}\), and by the Chain Rule, \[ \frac{dA}{dt} = \frac{dA}{d\theta}\frac{d\theta}{dt} = \frac12\theta'(t)r(t)^2 = \frac12 r(t)^2 \theta'(t) \] Thus, Kepler’s Second Law follows from the next theorem, which tells us that \(\frac{dA}{dt}\)has the constant value \(\frac12 \|{\bf J}\|\).
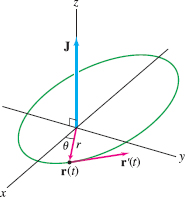
THEOREM 2
Let \(J=\|{\bf J}\|\) (\({\bf J}\) is constant by Theorem 1). Then \[ \boxed{\bbox[#FAF8ED,5pt]{r(t)^2\theta'(t) = J}}\tag{3} \]
Note
To compute cross products of vectors in the plane, such as \({\bf r}\), \({\bf e}_r\), and \({\bf e}_\theta\), we treat them as vectors in three-space with \(z\)-component equal to zero. The cross product is then a multiple of \({\bf k}\).
Proof
We note that in polar coordinates, \(\displaystyle{ {\bf e}_r = ( \cos\theta, \sin\theta )}\). We also define the unit vector \(\displaystyle{{\bf e}_\theta = ( {-}\sin\theta, \cos\theta )}\) that is orthogonal to \({\bf e}_r\) (Figure13.84). In summary, \[ \boxed{\bbox[#FAF8ED,5pt]{ r(t) = \|{\bf r}(t)\|,\quad {\bf e}_r = ( \cos\theta, \sin\theta ),\quad {\bf e}_\theta = ( -\sin\theta, \cos\theta ),\quad {\bf e}_r\cdot {\bf e}_\theta =0 }} \]
We see directly that the derivatives of \({\bf e}_r\) and \({\bf e}_\theta\) with respect to \(\theta\) are \[ \boxed{\bbox[#FAF8ED,5pt]{ \frac{d}{d\theta}{\bf e}_r = {\bf e}_{\theta},\qquad \frac{d}{d\theta}{\bf e}_\theta = -{\bf e}_r}}\tag{4} \]
The time derivative of \({\bf e}_r\) is computed using the Chain Rule: \[ {{\bf e}_r}' = \left(\frac{d\theta}{dt}\right)\left(\frac{d}{d\theta}{\bf e}_r\right) = \theta'(t)\,{\bf e}_\theta\tag{5} \]
Now apply the Product Rule to \({\bf r} = r{\bf e}_r\): \[ {\bf r}' = \frac{d}{dt}\,r{\bf e}_r = r'{\bf e}_{r}+ r {{\bf e}'}_r = r'{\bf e}_{r}+ r\theta'{\bf e}_\theta \]

768
Using \(\displaystyle{{\bf e}_r\times {\bf e}_{r} = {\bf 0}}\), we obtain \begin{align*} {\bf J} &= {\bf r}\times{\bf r}' = r{\bf e}_r\times (r'{\bf e}_{r}+ r\theta'{\bf e}_\theta) = r^2\theta'({\bf e}_r\times {\bf e}_{\theta}) \end{align*}
It is straightforward to check that \({\bf e}_r\times {\bf e}_{\theta}={\bf k}\), and since \({\bf k}\) is a unit vector, \(J=\|{\bf J}\| = |r^2\theta'|\). However, \(\theta'>0\) because the planet moves in the counterclockwise direction, so \(\displaystyle{J = r^2\theta'}\). This proves Theorem 2.
Proof of the Law of Ellipses
Let \({\bf v} = {\bf r}'(t)\) be the velocity vector. Then \({\bf r}'' = {\bf v}'\) and Eq. (1) may be written \[ \frac{d{\bf v}}{dt} = - \frac{k}{r(t)^2}\, {\bf e}_r\tag{6} \]
On the other hand, by the Chain Rule and the relation \(r(t)^2\theta'(t) =J\) of Eq. (3) \[ \frac{d{\bf v}}{dt} = \frac{d\theta}{dt} \frac{d{\bf v}}{d\theta}= \theta'(t)\frac{d{\bf v}}{d\theta} = \frac{J}{r(t)^2}\frac{d{\bf v}}{d\theta} \]
Together with Eq. (6), this yields \(\displaystyle{J\frac{d{\bf v}}{d\theta} = -k{\bf e}_r}\), or \[ \frac{d{\bf v}}\theta = -\frac{k}{J}{\bf e}_r = -\frac{k}{J}( \cos\theta, \sin\theta) \]
This is a first-order differential equation that no longer involves time \(t\). We can solve it by integration: \[ {\bf v} = -\frac{k}{J}\int( \cos\theta,\sin\theta)\,d\theta = \frac{k}{J}(-\sin\theta,\cos\theta ) + {\bf c} =\frac{k}{J}{\bf e}_\theta+ {\bf c}\tag{7} \] where \({\bf c}\) is an arbitrary constant vector.
We are still free to rotate our coordinate system in the plane of motion, so we may assume that \({\bf c}\) points along the \(y\)-axis. We can then write \({\bf c}= ( 0,(k/J)e)\) for some constant \(e\). We finish the proof by computing \({\bf J}={\bf r}\times{\bf v}\): \[ {\bf J} = {\bf r}\times{\bf v} = r{\bf e}_r\times \left(\frac{k}{J}{\bf e}_\theta + {\bf c}\right) = \frac{k}{J}r\big({\bf e}_r\times {\bf e}_{\theta} + {\bf e}_r\times ( 0,e)\big) \]
Direct calculation yields \[ {\bf e}_r\times {\bf e}_{\theta}={\bf k},\qquad {\bf e}_r\times ( 0,e) = (e\cos\theta){\bf k} \] so our equation becomes \(\displaystyle{{\bf J} = \frac{k}{J}r (1 + e\cos\theta ){\bf k}}\). Since \({\bf k}\) is a unit vector, \[ J = \|{\bf J}\| = \frac{k}{J}r\big(1+e\cos\theta\big) \]
Solving for \(r\), we obtain the polar equation of a conic section of eccentricity \(e\) (an ellipse, parabola, or hyperbola): \[ r = \frac{J^2/k}{1+e\cos\theta} \]
This result shows that if a planet travels around the sun in a bounded orbit, then the orbit must be an ellipse. There are also “open orbits” that are either parabolic and hyperbolic. They describe comets that pass by the sun and then continue into space, never to return. In our derivation, we assumed implicitly that \({\bf J}\ne \mathbf{0}\). If \({\bf J}={\bf 0}\), then \(\theta'(t)=0\). In this case, the orbit is a straight line, and the planet falls directly into the sun.
Kepler’s Third Law is proven in the exercises.
Question 13.362 Section 13.8 Progress Check Question 1
One of Kepler's laws of Planetary Motion states that the orbit of a planet in our solar system is with the sun at .
769
Real-Life Trajectories
Interesting paths in \({\mathbb R}^{3}\) that obey Newton’s second law occur in our own solar system and are used by NASA to plan space missions. One such mission, the Genesis Discovery Mission, launched from earth August 8, 2001, has a particularly interesting trajectory, as shown in Figure 13.8. More information about this trajectory and the mission objectives can be found at https://genesismission.jpl.nasa.gov/.
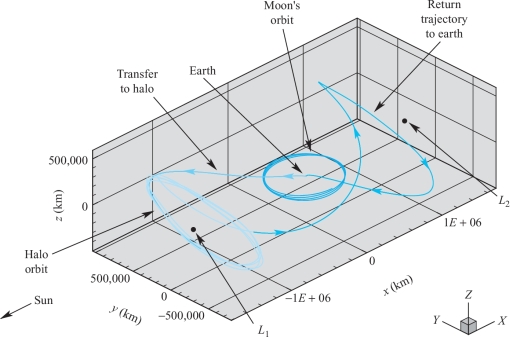
The points denoted \(L_{1}\) and \(L_{2}\) in this figure denote places of balance (discovered by Euler) between the earth and the sun. A motionless spacecraft positioned there will remain there. There are periodic orbits about these points that we have (loosely) called halo orbits. The main dynamics of the spacecraft is governed by the pull of both the earth and the sun (and to a very small extent the moon) on the spacecraft. This is thus part of the famous three-body problem studied and made famous by Poincaré around 1890. For more information about Poincaré see F. Diacu and P. Holmes, Celestial Encounters. The Origin of Chaos and Stability , Princeton University Press: Princeton, NJ 1996.
HISTORICAL PERSPECTIVE

The astronomers of the ancient world (Babylon, Egypt, and Greece) mapped out the nighttime sky with impressive accuracy, but their models of planetary motion were based on the erroneous assumption that the planets revolve around the earth. Although the Greek astronomer Aristarchus (310‒230 bce) had suggested that the earth revolves around the sun, this idea was rejected and forgotten for nearly eighteen centuries, until the Polish astronomer Nicolaus Copernicus (1473‒1543) introduced a revolutionary set of ideas about the solar system, including the hypothesis that the planets revolve around the sun. Copernicus paved the way for the next generation, most notably Tycho Brahe (1546‒1601), Galileo Galilei (1564‒1642), and Johannes Kepler (1571‒1630).
Constants
- Gravitational constant: \[G \approx 6.673 \times 10^{-11} \mathrm{m}^3\,\mathrm{kg}^{-1}\,\mathrm{s}^{-2}\]
- Mass of the sun: \[M\approx 1.989\times 10^{30} \mathrm{kg}\]
- \(k=GM\approx 1.327\times 10^{20}\)
The German astronomer Johannes Kepler was the son of a mercenary soldier who apparently left his family when Johannes was 5 and may have died at war. He was raised by his mother in his grandfather’s inn. Kepler’s mathematical brilliance earned him a scholarship at the University of Tübingen and at age of 29, he went to work for the Danish astronomer Tycho Brahe, who had compiled the most complete and accurate data on planetary motion then available. When Brahe died in 1601, Kepler succeeded him as “Imperial Mathematician” to the Holy Roman Emperor, and in 1609 he formulated the first two of his laws of planetary motion in a work entitled Astronomia Nova (New Astronomy).
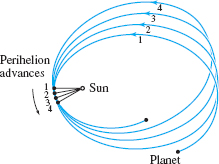
In the centuries since Kepler’s death, as observational data improved, astronomers found that the planetary orbits are not exactly elliptical. Furthermore, the perihelion (the point on the orbit closest to the sun) shifts slowly over time (Figure 13.86). Most of these deviations can be explained by the mutual pull of the planets, but the perihelion shift of Mercury is larger than can be accounted for by Newton’s Laws. On November 18, 1915,Albert Einstein made a discovery about which he later wrote to a friend, “I was beside myself with ecstasy for days.”He had been working for a decade on his famous General Theory of Relativity, a theory that would replace Newton’s law of gravitation with a new set of much more complicated equations called the Einstein Field Equations. On that 18th of November, Einstein showed that Mercury’s perihelion shift was accurately explained by his new theory. At the time, this was the only substantial piece of evidence that the General Theory of Relativity was correct. We will discuss Einstein's work in more detail in Section 17.7.