exercises
In Exercises 1 to 16, find the critical points of the given function and then determine whether they are local maxima, local minima, or saddle points.
Question 3.46
\(f(x,y) = x^2 - y^2 + xy\)
Question 3.47
\(f(x,y) = x^2 + y^2 - xy\)
Question 3.48
\(f(x,y) = x^2 + y^2 + 2xy\)
Question 3.49
\(f(x,y) = x^2 + y^2 + 3xy\)
Question 3.50
\(f(x,y) = e^{1+x^2 - y^2}\)
Question 3.51
\(f(x,y) = x^2 - 3xy + 5x - 2y + 6y^2 + 8\)
Question 3.52
\(f(x,y) = 3x^2 + 2xy + 2x + y^2 + y+4\)
Question 3.53
\(f(x,y) = \sin\,(x^2 + y^2)\) [consider only the critical point \((0,0)\)]
Question 3.54
\(f(x,y) = \cos\,(x^2 + y^2)\) [consider only the three critical points \((0,0), (\sqrt{\pi/2},\sqrt{\pi/2})\), and \((0,\sqrt{\pi})\)]
183
Question 3.55
\(f(x,y) = y + x\sin y\)
Question 3.56
\(f(x,y) = e^x \cos y\)
Question 3.57
\(f(x,y) = (x-y)(xy-1)\)
Question 3.58
\(f(x,y) = xy + {\displaystyle\frac{1}{x}}+ {\displaystyle\frac{1}{y}}\)
Question 3.59
\(f(x,y) = \log\,(2+\sin xy)\)
Question 3.60
\(f(x,y) = x\sin y\)
Question 3.61
\(f(x,y) = (x+y)(xy+1)\)
Question 3.62
Find all local extrema for \(f(x, y)=8y^3+12x^2-24xy\).
Question 3.63
Let \(f(x, y, z)=x^2 +y^2 +z^2+kyz\).
- (a) Verify that (0, 0, 0) is a critical point for \(f\).
- (b) Find all values of \(k\) such that \(f\) has a local minimum at (0, 0, 0).
Question 3.64
Find and classify all critical points of \(f(x, y)= \frac{1}{3}x^3 +\frac{1}{3}y^3 - \frac{1}{2}x^2 -\frac{5}{2}y^2+6y+10\).
Question 3.65
Suppose (4, 2) is a critical point for the \(C^2\) function \(f(x, y)\). In each case, determine whether (4, 2) is a local maximum, a local minimum, or a saddle point.
- (a) \(f_{xx}(4, 2)= 1, \ f_{xy}(4, 2)=3, \ f_{yy}=5\)
- (b) \(f_{xx}(4, 2)= 2, \ f_{yx}(4, 2)=-1, \ f_{yy}=4\)
- (c) \(f_{xx}(4, 2)= -2, \ f_{xy}(4, 2)=1, \ f_{yy}=3\)
Question 3.66
Find the local maxima and minima for \(z=(x^2+3y^2)\,e^{1-x^2-y^2}\). (See Figure 2.1.15.)
Question 3.67
Let \(f(x,y)=x^2+y^2+kxy\). If you imagine the graph changing as \(k\) increases, at what values of \(k\) does the shape of the graph change qualitatively?
Question 3.68
An examination of the function \(f{:}\, \,{\mathbb R}^2 \to {\mathbb R}, (x,y) \mapsto (y-3x^2)(y-x^2)\) will give an idea of the difficulty of finding conditions that guarantee that a critical point is a relative extremum when Theorem 6 fails.footnote # Show that
- (a) the origin is a critical point of \(f\);
- (b) \(f\) has a relative minimum at \((0, 0)\) on every straight line through \((0, 0)\); that is, if \(g(t) = (at,bt)\), then \(f\circ g{:}\,\, {\mathbb R} \to {\mathbb R}\) has a relative minimum at 0, for every choice of \(a\) and \(b\);
- (c) the origin is not a relative minimum of \(f\).
Question 3.69
Let \(f(x,y)= Ax^2 + E\), where \(A\) and \(E\) are constants. What are the critical points of \(f\)? Are they local maxima or local minima?
Question 3.70
Let \(f(x,y) = x^2 - 2xy + y^2\). Here \(D=0\). Can you say whether the critical points are local minima, local maxima, or saddle points?
Question 3.71
Let \(f(x, y)=ax^2+bx^2\), where \(a, b \neq 0\).
- (a) Show that (0, 0) is the only critical point for \(f\).
- (b) Determine the nature of this critical point in terms of \(a\) and \(b\).
Question 3.72
Suppose \(f \colon \mathbb{R}^3 \to \mathbb{R}\) is \(C^2\), and that \(\textbf{x}_0\) is a critical point for \(f\). Suppose \({\it Hf}(\textbf{x}_0)(\textbf{h}) = h_1^2+h_2^2+h_3^2+4h_2h_3\). Does \(f\) have a local maximum, minimum, or saddle at \(\textbf{x}_0\)?
Question 3.73
Find the point on the plane \(2x-y+2z = 20\) nearest the origin.
Question 3.74
Show that a rectangular box of given volume has minimum surface area when the box is a cube.
Question 3.75
Show that the rectangular parallelepiped with fixed surface area and maximum volume is a cube.
Question 3.76
Write the number 120 as a sum of three numbers so that the sum of the products taken two at a time is a maximum.
Question 3.77
Show that if \((x_0,y_0)\) is a critical point of a quadratic function \(f(x,y)\) and \(D<0\), then there are points \((x,y)\) near \((x_0,y_0)\) at which \(f(x,y) > f(x_0,y_0)\) and, similarly, points for which \(f(x,y) < f(x_0,y_0)\).
Question 3.78
Let \(f(x, y)=x^6+x^2+y^6, \; g(x, y)=-x^6-x^2-y^6, \; h(x, y)=x^6-x^4+y^6\).
- (a) Show that (0, 0) is a degenerate critical point for \(f, g\), and \(h\).
- (b) Show that (0, 0) is a local minimum for \(f\), a local maximum for \(g\), and a saddle for \(h\).
Question 3.79
Let \(f(x, y)=5ye^x-e^{5x}-y^5\).
- (a) Show that \(f\) has a unique critical point and that this point is a local maximum for \(f\).
- (b) Show that \(f\) is unbounded on the \(y\) axis, and thus has no global maximum. [Note that for a function \(g(x)\) of a single variable, a unique critical point which is a local extremum is necessarily a global extremum. This example shows that this is not the case for functions of several variables.]
184
Question 3.80
Determine the nature of the critical points of the function \[ f(x,y,z) = x^2 + y^2 + z^2 + xy. \]
Question 3.81
Let \(n\) be an integer greater than 2 and set \(f(x,y) = ax^n + cy^n\), where \(ac\neq 0\). Determine the nature of the critical points of \(f\).
Question 3.82
Determine the nature of the critical points of \(f(x,y) = x^3 + y^2 - 6xy + 6x + 3y\).
Question 3.83
Find the absolute maximum and minimum values of the function \(f(x,y) = (x^2 + y^2)^4\) on the disc \(x^2 + y^2 \le 1\). (You do not have to use calculus.)
Question 3.84
Repeat Exercise 38 for the function \(f(x,y) = x^2 + xy + y^2\).
Question 3.85
A curve \(C\) in space is defined implicitly on the cylinder \(x^2 + y^2 =1\) by the additional equation \(x^2 - xy + y^2 - z^2 = 1\). Find the point or points on \(C\) closest to the origin.
Question 3.86
Find the absolute maximum and minimum values for \(f(x,y) = \sin x + \cos y\) on the rectangle \(R\) defined by \(0 \le x \le 2\pi, 0 \le y \le 2\pi\).
Question 3.87
Find the absolute maximum and minimum values for the function \(f(x,y) = xy\) on the rectangle \(R\) defined by \(-1 \le x \le 1, -1 \le y\le 1\).
Question 3.88
Let \(f(x, y)=1+xy-2x+y\) and let \(D\) be the triangular region in \(\mathbb R^2\) with vertices (\(-2\), 1), (\(-2\), 5), and (2, 1). Find the absolute maximum and minimum values of \(f\) on \(D\). Give all points where these extreme values occur.
Question 3.89
Let \(f(x, y)=1+xy+x-2y\) and let \(D\) be the triangular region in \(\mathbb R^2\) with vertices (1, \(-2\)), (5, \(-2\)), and (1, 2). Find the absolute maximum and minimum values of \(f\) on \(D\). Give all points where these extreme values occur.
Question 3.90
Determine the nature of the critical points of \(f(x,y) = xy + 1/x + 8/y\).
In Exercises 46 through 50, D denotes the unit disc.
Question 3.91
Let \(u\) be a \(C^2\) function on \(D\) which is “strictly subharmonic”; that is, the following inequality holds: \(\nabla^2u = (\partial^2u/\partial x^2) + (\partial^2u/\partial y^2) > 0\). Show that \(u\) cannot have a maximum point in \(D\backslash \partial D\) (the set of points in \(D\), but not in \(\partial D\)).
Question 3.92
Let \(u\) be a harmonic function on \(D\)—that is, \(\nabla^2 u = 0\) on \(D\backslash\partial D\)—and be continuous on \(D\). Show that if \(u\) achieves its maximum value in \(D\backslash \partial D\), it also achieves it on \(\partial D\). This is sometimes called the “weak maximum principle” for harmonic functions. [HINT: Consider \(\nabla^2(u + \varepsilon e^x), \varepsilon > 0\). You can use the following fact, which is proved in more advanced texts: Given a sequence \(\{{\bf p}_n\},\,n\,{=}\,1,2,\ldots,\) of points in a closed bounded set \(A\) in \({\mathbb R}^2\) or \({\mathbb R}^3\), there exists a point \({\bf q}\) such that every neighborhood of \({\bf q}\) contains infinitely many members of \(\{{\bf p}_n\}\).]
Question 3.93
Define the notion of a strict superharmonic function \(u\) on \(D\) by mimicking Exercise 46. Show that \(u\) cannot have a minimum in \(D\backslash \partial D\).
Question 3.94
Let \(u\) be harmonic in \(D\) as in Exercise 47. Show that if \(u\) achieves its minimum value in \(D\backslash\partial D\), it also achieves it on \(\partial D\). This is sometimes called the “weak minimum principle” for harmonic functions.
Question 3.95
Let \(\phi{:}\,\, \partial D\to {\mathbb R}\) be continuous and let \(T\) be a solution on \(D\) to \(\nabla^2T = 0,\) continuous on \(D\) and \(T = \phi\) on \(\partial D\).
- (a) Use Exercises 46 to 49 to show that such a solution, if it exists, must be unique.
- (b) Suppose that \(T(x,y)\) represents a temperature function that is independent of time, with \(\phi\) representing the temperature of a circular plate at its boundary. Can you give a physical interpretation of the principle stated in part (a)?
Question 3.96
- (a) Let \(f\) be a \(C^1\) function on the real line \({\mathbb R}\). Suppose that \(f\) has exactly one critical point \(x_0\) that is a strict local minimum for \(f\). Show that \(x_0\) is also an absolute minimum for \(f\); that is, that \(f(x) \ge f(x_0)\) for all \(x\).
(b) The next example shows that the conclusion of part (a) does not hold for functions of more than one variable. Let \(f{:}\,\, {\mathbb R}^2 \to {\mathbb R}\) be defined by \[ f(x,y) = -y^4-e^{-x^2} + 2y^2 {\textstyle\sqrt{e^x + e^{-x^2}}}. \]
(i)\(\quad\) Show that \((0, 0)\) is the only critical point for \(f\) and that it is a local minimum.
(ii)\(\quad\) Argue informally that \(f\) has no absolute minimum.
185
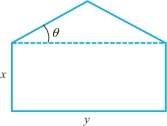
Question 3.97
Suppose that a pentagon is composed of a rectangle topped by an isosceles triangle (see Figure 3.13). If the length of the perimeter is fixed, find the maximum possible area.