13.5 Gradients and Directional Derivatives
135
In Section 13.1 we studied the graphs of real-valued functions. Now in this section we take up this study again, using the methods of calculus. Specifically, gradients will be used to obtain a formula for the plane tangent to a level surface.
Gradients in ℝ³
Let us recall the definition.
Definition: The Gradient
If \(f\colon\, U\subset {\mathbb R}^3\to {\mathbb R}\) is differentiable, the gradient of \(f\) at \((x,y,z)\) is the vector in space given by \[ \nabla f=\bigg( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \bigg). \]
This vector is also denoted \({\nabla} f(x,y,z)\). Thus, \({\nabla} f\) is just the matrix of the derivative \({\bf D} f\), written as a vector.
example 1
Let \(f(x,y,z)=\sqrt{x^2+y^2+z^2}=r\), the distance from \({\bf 0}\) to \((x,y,z)\). Then \begin{eqnarray*} \nabla f(x,y,z)&=&\bigg( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \bigg)\\[3pt] &=&\bigg(\frac{x}{\sqrt{x^2+y^2+z^2}},\frac{y}{\sqrt{x^2+y^2+z^2}},\frac{z}{\sqrt{x^2+y^2+z^2}}\bigg) =\frac{{\bf r}}{r}, \end{eqnarray*} where \({\bf r}\) is the point \((x,y,z)\). Thus, \(\nabla f\) is the unit vector in the direction of \((x,y,z)\).
example 2
If \(f(x,y,z)=xy+z,\) then \[ \nabla f(x,y,z)=\bigg( \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} \bigg)=(y,x,1). \]
Question 13.155 Section 13.5 Progress Check Question 1
Find the gradient \(\nabla f\) of \(f(x,y,z) = x+y^2-y e^z\)
| A. |
| B. |
| C. |
| D. |
| E. |
Directional Derivatives
136
Suppose \(f\colon\, {\mathbb R}^3\to{\mathbb R}\) is a real-valued function. Let v and \({\bf x}\in {\mathbb R}^3\) be fixed vectors and consider the function from \({\mathbb R}\) to \({\mathbb R}\) defined by \(t\mapsto f({\bf x}+t{\bf v})\). The set of points of the form \({\bf x}+t{\bf v}, t\in {\mathbb R}\), is the line \(L\) through the point \({\bf x}\) parallel to the vector \({\bf v}\) (see Figure 13.46).
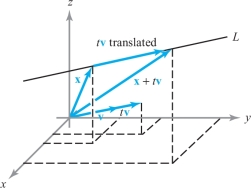
The function \(t\mapsto f({\bf x}+t{\bf v})\) represents the function \(f\) restricted to the line \(L\). For example, if a bird flies along this line with velocity \({\bf v}\) so that \({\bf x} + t{\bf v}\) is its position at time \(t\), and if \(f\) represents the temperature as a function of position, then \(f({\bf x}+t{\bf v})\) is the temperature at time \(t\). We may ask: How fast are the values of \(f\) changing along the line \(L\) at the point \({\bf x}\)? Because the rate of change of a function is given by a derivative, we could say that the answer to this question is the value of the derivative of this function of \(t\) at \(t=0\) (when \(t=0,{\bf x}+t{\bf v}\) reduces to \({\bf x}\)). This would be the derivative of \(f\) at the point \({\bf x}\) in the direction of \(L\); that is, of \({\bf v}\). We can formalize this concept as follows.
Definition: Directional Derivatives
If \(f\colon\, {\mathbb R}^3\to {\mathbb R},\) the directional derivative of \(f\) at x along the vector v is given by \[ \frac{d}{dt}f({\bf x}+t{\bf v}) \bigg|_{t=0} \] if this exists.
In the definition of a directional derivative, we normally choose v to be a unit vector. In this case, we are moving in the direction \({\bf v}\) with unit speed and we refer to \(\frac{d}{dt}f({\bf x}+t{\bf v}) \big|_{t=0}\) as the directional derivative of f in the direction \({\bf v}\).
We now elaborate on why a unit vector is chosen in the definition of the directional derivative. Suppose that \(f\) measures the temperature in degrees and that we are interested in how fast the temperature changes as we move in a particular direction. If we are measuring distance in meters, then the rate of change of temperature will be measured in degrees per meter. Suppose, for simplicity, that the temperature is changing at a constant rate—say, two degrees per meter—as we move in a given direction v starting at x. Thus, when we go one meter ahead, the temperature changes by two degrees. That is, \[ f({\bf x} + {\bf v}) - f({\bf x}) = 2. \]
Such a relation is going to hold only when v is a unit vector, reflecting the fact that we are going ahead by one meter. More generally, the definition of the directional derivative is going to truly measure only the rate of change of \(f\) with respect to distance along a line in a given direction if v is a unit vector.
From the definition, we can see that the directional derivative can also be defined by the formula \[ \mathop {{\rm limit}}_{h\to 0}\frac{f({\bf x}+h{\bf v})- f({\bf x})}{h}. \]
Theorem 12
If \(f\colon\, {\mathbb R}^3\to {\mathbb R}\) is differentiable, then all directional derivatives exist. The directional derivative at x in the direction v is given by \[ {\bf D} f({\bf x}){\bf v}={\rm grad}f({\bf x})\,{ \cdot}\, {\bf v} = \nabla f({\bf x})\,{ \cdot}\,{\bf v} =\bigg[\frac{\partial f}{\partial x}({\bf x}) \bigg]v_1+ \bigg[\frac{\partial f}{\partial y}({\bf x})\bigg]v_2+ \bigg[\frac{\partial f}{\partial z}({\bf x})\bigg]v_3, \] where \({\bf v}=(v_1,v_2,v_3)\).
137
proof
Let \({\bf c}(t)={\bf x}+t{\bf v}\), so that \(f({\bf x}+t{\bf v})=f({\bf c}(t))\). By the first special case of the chain rule, \((d/dt)f({\bf c}(t))= \nabla f({\bf c}(t)) \,{\cdot}\, {\bf c}'(t)\). However, \({\bf c}(0)={\bf x}\) and \({\bf c}'(0)={\bf v}\), and so \[ \frac{d}{dt}f({\bf x}+t{\bf v}) \bigg|_{t=0}= \nabla f({\bf x}) \,{\cdot}\, {\bf v}, \] as we were required to prove.
Notice that one does not have to use straight lines when computing the rate of change of \(f\) in a specific direction \({\bf v}\). Indeed, for a general path \({\bf c}(t)\) with \({\bf c}(0)={\bf x}\) and \({\bf c}'(0)={\bf v}\), we have from the chain rule, \[ \frac{d}{dt}f({\bf c}(t))\bigg|_{t=0}=\nabla f({\bf c}(t))\,{\cdot}\,{\bf c}'(t)\bigg|_{t=0}=\nabla f({\bf x}) \,{ \cdot}\, {\bf v}. \]
example 3
Let \(f(x,y,z)=x^2e^{-yz}\). Compute the rate of change of \(f\) in the direction of the unit vector \[ {\bf v}=\bigg(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\bigg) \qquad\hbox{at the point }\qquad (1,0,0). \]
solution The required rate of change is, using Theorem 12, \[ \nabla f\, { \cdot}\, {\bf v}=(2xe^{-yz},-x^2ze^{-yz}, -x^2ye^{-yz})\,{ \cdot}\, \bigg(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}\bigg), \] which, at the point (1, 0, 0), becomes \[ (2,0,0)\,{\cdot}\,\bigg(\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\bigg)=\frac{2}{\sqrt{3}}. \]
example 4
In the last example, find the rate of change of \(f\) in the direction of the vector \({\bf w}=(1,1,1)\).
solution \({\bf w}\) is not a unit vector. Replacing \({\bf w}\) by \[ {\bf v}=\frac{{\bf w}}{\|{\bf w}\|}= \left(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}\right) \] and proceeding as in Example 3, we again obtain \(\,{2}/{\sqrt{3}}\,\) as our answer.
Question 13.156 Section 13.5 Progress Check Question 2
Let \(f(x,y,z)= x^2-y^2+2z\). Compute the rate of change of \(f\) in the direction of the vector \((\sqrt{2},-1,1)\) at the point \((0,1,2)\).
Directions of Fastest Increase
From Theorem 12 we can also obtain the geometric significance of the gradient:
Theorem 13
Assume \(\nabla f({\bf x})\not={\bf 0}\). Then \(\nabla f({\bf x})\) points in the direction along which \(f\) is increasing the fastest.
proof
If n is a unit vector, the rate of change of \(f\) in direction n is given by \(\nabla f({\bf x})\, {\cdot}\, {\bf n} = \|\nabla f({\bf x})\| \cos \theta\), where \(\theta\) is the angle between \({\bf n}\) and \(\nabla f({\bf x})\). This is maximum when \(\theta =0\); that is, when n and \(\nabla f\) are parallel. [If \(\nabla f({\bf x})={\bf 0}\) this rate of change is 0 for any \({\bf n}\).]
138
In other words, if we wish to move in a direction in which \(f\) will increase most quickly, we should proceed in the direction \(\nabla f({\bf x})\). Analogously, if we wish to move in a direction in which \(f\) decreases the fastest, we should proceed in the direction \(- \nabla f({\bf x})\).
example 5
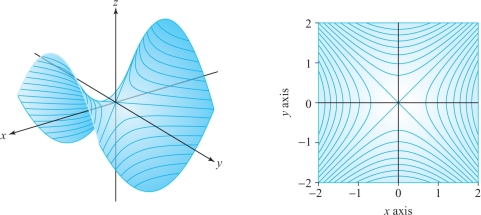
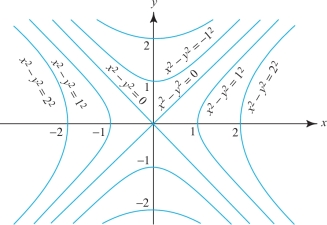
In what direction from \((0, 1)\) does \(f(x,y)=x^2-y^2\) increase the fastest?
solution The gradient is \[ \nabla f=2x{\bf i}-2y{\bf j}, \] and so at (0, 1) this is \[ \nabla f \big|_{(0,1)}=-2{\bf j}. \]
By Theorem 13, \(f\) increases fastest in the direction \(-{\bf j}\). (Can you see why this answer is consistent with Figure 13.47 and Figure 13.48?)
Gradients and Tangent Planes to Level Sets
Now we find the relationship between the gradient of a function \(f\) and its level surfaces. The gradient points in the direction in which the values of \(f\) change most rapidly, whereas a level surface lies in the directions in which they do not change at all. If \(f\) is reasonably well behaved, the gradient and the level surface will be perpendicular.
Theorem 14 The Gradient is Normal to Level Surfaces
Let \(f\colon\, {\mathbb R}^3\to {\mathbb R}\) be a \(C^1\) map and let \((x_0,y_0,z_0)\) lie on the level surface \(S\) defined by \(f(x,y,z)=k,\) for \(k\) a constant. Then \(\nabla f(x_0,y_0,z_0)\) is normal to the level surface in the following sense: If v is the tangent vector at \(t=0\) of a path \({\bf c}(t)\) in \(S\) with \({\bf c}(0)=(x_0,y_0,z_0),\) then \({\nabla } f (x_0, y_0, z_0)\,{ \cdot}\,{\bf v}=0\) (see Figure 13.49).
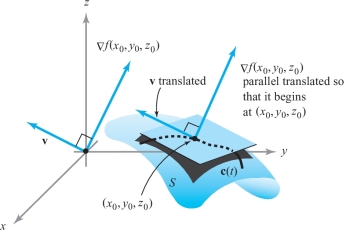
proof
Let \({\bf c}(t)\) lie in \(S\); then \(f({\bf c}(t))=k\). Let \({\bf v}\) be as in the hypothesis; then \({\bf v}={\bf c}'(0)\). Hence, the fact that \(f({\bf c}(t))\) is constant in \(t\), and the chain rule give \[ 0=\frac{d}{dt}f({\bf c}(t))\bigg|_{t=0}= \nabla f({\bf c}(0)) \,{ \cdot}\, {\bf v}. \]
139
If we study the conclusion of Theorem 14, we see that it is reasonable to define the plane tangent to \(S\) as the orthogonal plane to the gradient.
Definition: Tangent Planes to Level Surfaces
Let \(S\) be the surface consisting of those \((x,y,z)\) such that \(f(x,y,z)=k,\) for \(k\) a constant. The tangent plane of \(S\) at a point \((x_0,y_0,z_0)\) of \(S\) is defined by the equation \begin{equation*} \nabla f (x_0,y_0,z_0)\, { \cdot}\, (x-x_0,y-y_0,z-z_0)= 0\tag{1} \end{equation*} if \(\nabla f(x_0,y_0,z_0) \not={\bf 0}\). That is, the tangent plane is the set of points \((x,y,z)\) that satisfy equation (1).
This extends the definition we gave earlier for the tangent plane of the graph of a function (see Exercise 15 at the end of this section).
example 6
Compute the equation of the plane tangent to the surface defined by \(3xy+z^2=4\) at \((1,1,1)\).
solution Here \(f(x,y,z)=3xy+z^2\) and \(\nabla f=(3y,3x,2z)\), which at \((1, 1, 1)\) is the vector \((3, 3, 2)\). Thus, the tangent plane is \[ (3,3,2) \,{ \cdot}\, (x-1,y-1,z-1)=0; \] that is, \[ 3x+3y+2z =8. \]
Question 13.157 Section 13.5 Progress Check Question 3
Compute the equation of the plane tangent to the surface defined by \(x^2-y^2-z+2=0\) at \((1,-1,2)\).
| A. |
| B. |
| C. |
| D. |
| E. |
In Theorem 14 and the definition following it, we could just as well have worked in two dimensions as in three. Thus, if we have \(f\colon\, {\mathbb R}^2\to {\mathbb R}\) and consider a level curve \[ C=\{(x,y) \mid f(x,y)=k\}, \] then \(\nabla f(x_0,y_0)\) is perpendicular to \(C\) for any point \((x_0,y_0)\) on \(C\). Likewise, the tangent line to \(C\) at \((x_0,y_0)\) has the equation \begin{equation*} \nabla f(x_0,y_0) \,{ \cdot}\, (x-x_0,y-y_0)=0\tag{2} \end{equation*} if \(\nabla f(x_0,y_0)\not= {\bf 0}\); that is, the tangent line is the set of points \((x,y)\) that satisfy equation (2) (see Figure 13.50).
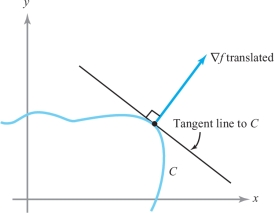
The Gradient Vector Field
140
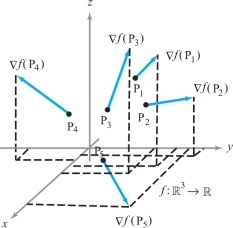
We often speak of \(\nabla f\) as a gradient vector field. The word “field” means that \(\nabla f\) assigns a vector to each point in the domain of \(f\). In Figure 13.51 we describe the gradient \(\nabla f\) not by drawing its graph, which, if \(f\colon\,{\mathbb R}^3\to {\mathbb R}\), would be a subset of \({\mathbb R}^6\)—that is, the set of tuples \(({\bf x}, \nabla f({\bf x}))\), but by representing \(\nabla f({\rm P})\), for each point P, as a vector emanating from the point P rather than from the origin. Like a graph, this pictorial method of depicting \(\nabla f\) contains the point P and the value \(\nabla f({\rm P})\) in the same picture.
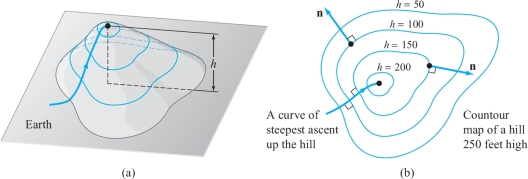
The gradient vector field has important geometric significance. It shows the direction in which \(f\) is increasing the fastest and the direction that is orthogonal to the level surfaces (or curves in the plane) of \(f\). That it does both of these at once is quite plausible. To see this, imagine a hill as shown in Figure 13.52. Let \(h\) be the height function, a function of two variables. If we draw level curves of \(h\), these are just level contours of the hill. We could imagine them as level paths on the hill [see Figure 13.52]. One thing should be obvious to anyone who has gone for a hike: To get to the top of the hill the fastest, we should walk perpendicular to level contours.footnote # This is consistent with Theorems 13 and 14, which state that the direction of fastest increase (the gradient) is orthogonal to the level curves.
141
example 7
The gravitational force on a unit mass \(m\) at \((x,y,z)\) produced by a mass \(M\) at the origin in \({\mathbb R}^3\) is, according to Newton’s law of gravitation, given by \[ {\bf F}=-\frac{GmM}{r^2}{\bf n}, \] where \(G\) is a constant; \(r= \| {\bf r} \| =\sqrt{x^2+y^2+z^2},\) which is the distance of \((x,y,z)\) from the origin; and \({\bf n}={\bf r}/r,\) the unit vector in the direction of \({\bf r}=x{\bf i}+y{\bf j}+z{\bf k},\) which is the position vector from the origin to \((x,y,z)\).
Note that \({\bf F}= \nabla (GmM/r)=- \nabla V\); that is, \({\bf F}\) is the negative of the gradient of the gravitational potential \(V=-GmM/r\). This can be verified as in Example \(1\). Notice that \({\bf F}\) is directed inward toward the origin. Also, the level surfaces of \(V\) are spheres. The gradient vector field F is normal to these spheres, which confirms the result of Theorem 14.
example 8
Find a unit vector normal to the surface \(S\) given by \(z=x^2y^2+y+1\) at the point \((0, 0, 1)\).
solution Let \(f(x,y,z)=x^2y^2+y+1-z\), and consider the level surface defined by \(f(x,y,z)=0\). Because this is the set of points \((x,y,z)\) with \(z=x^2y^2+y+1\), we see that this level set coincides with the surface \(S\). The gradient is given by \[ \nabla f(x,y,z) = \frac{\partial f}{\partial x}{\bf i}+\frac{\partial f}{\partial y}{\bf j}+\frac{\partial f}{\partial z}{\bf k}= 2xy^2{\bf i}+(2x^2y+1){\bf j}-{\bf k}, \] and so \[ \nabla f(0,0,1)={\bf j}-{\bf k}. \]
This vector is perpendicular to \(S\) at (0, 0, 1), and so to find a unit normal n we divide this vector by its length to obtain \[ {\bf n}=\frac{ \nabla f(0,0,1)}{ \| \nabla f(0,0,1) \| }=\frac{1}{\sqrt{2}}(\,{\bf j}-{\bf k}). \]
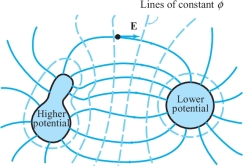
example 9
Consider two conductors, one charged positively and the other negatively. Between them, an electric potential is set up. This potential is a function \(\phi\colon \,{\mathbb R}^3\to {\mathbb R}\) (an example of a scalar field). The electric field is given by \({\bf E}=- \nabla \phi\). From Theorem \(14\) we know that E is perpendicular to level surfaces of \(\phi\). These level surfaces are called equipotential surfaces, because the potential is constant on them (see Figure 13.53).