exercises
Find the divergence of the vector fields in Exercises 1 to 4.
Question 4.80
\({\bf V}(x,y,z)=e^{xy}{\bf i}-e^{xy}{\bf j}+e^{yz}{\bf k}\)
Question 4.81
\({\bf V} (x,y,z)=yz{\bf i}+xz{\bf j}+xy{\bf k}\)
Question 4.82
\({\bf V}(x,y,z)=x{\bf i}+(y+\cos x){\bf j}+(z+e^{xy}){\bf k}\)
Question 4.83
\({\bf V}(x,y,z)=x^2{\bf i}+(x+y)^2{\bf j}+(x+y+z)^2{\bf k}\)
Question 4.84
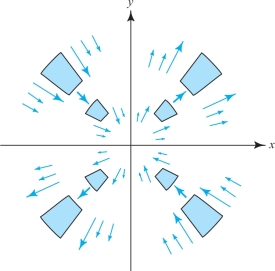
Figure 4.41 shows some flow lines and moving regions for a fluid moving in the plane-field velocity field \({\bf V}\). Where is div \({\bf V} > 0\), and also where is div \({\bf V} < 0\)?
Question 4.85
Let \(V(x,y,z)=x{\bf i}\) be the velocity field of a fluid in space. Relate the sign of the divergence with the rate of change of volume under the flow.
Question 4.86
Sketch a few flow lines for \({\bf F}(x,y)=y{\bf i}\). Calculate \(\nabla\,{\cdot}\, {\bf F}\) and explain why your answer is consistent with your sketch.
Question 4.87
Sketch a few flow lines for \({\bf F}(x,y)=-3x{\bf i}-y{\bf j}\). Calculate \(\nabla \,{\cdot}\, {\bf F}\) and explain why your answer is consistent with your sketch.
259
Calculate the divergence of the vector fields in Exercises 9 to 12.
Question 4.88
\({\bf F}(x,y)=x^3{\bf i}-x\sin\, (xy){\bf j}\)
Question 4.89
\({\bf F}(x,y)=y{\bf i}-x{\bf j}\)
Question 4.90
\({\bf F}(x,y)=\sin\, (xy){\bf i} -\cos\, (x^2y){\bf j}\)
Question 4.91
\({\bf F}(x,y)=xe^y{\bf i}-[\,y/(x+y)]{\bf j}\)
Compute the curl, \(\nabla \times {\bf F}\), of the vector fields in Exercises 13 to 16.
Question 4.92
\({\bf F}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}\)
Question 4.93
\({\bf F}(x,y,z)=yz{\bf i}+xz{\bf j}+xy{\bf k}\)
Question 4.94
\({\bf F}(x,y,z)=(x^2+y^2+z^2)(3{\bf i}+4{\bf j}+5{\bf k})\)
Question 4.95
\({\bf F}(x,y,z)=\displaystyle\frac{yz{\bf i}-xz{\bf j}+xy{\bf k}}{x^2+y^2+z^2}\)
Calculate the scalar curl of each of the vector fields in Exercises 17 to 20.
Question 4.96
\({\bf F}(x,y)=\sin x{\bf i}+\cos x{\bf j}\)
Question 4.97
\({\bf F}(x,y)=y{\bf i}-x{\bf j}\)
Question 4.98
\({\bf F}(x,y)=xy{\bf i}+(x^2-y^2){\bf j}\)
Question 4.99
\({\bf F}(x,y)=x{\bf i}+y{\bf j}\)
Question 4.100
Let \(\textbf{F}(x,y,z)=(x^2,x^2y,z+zx)\).
- (a) Verify that \(\nabla \cdot (\nabla \times \textbf{F}) =0\).
- (b) Can there exist a function \(f \colon \mathbb R^3 \to \mathbb R\) such that \(\textbf{F}=\nabla f\)? Explain.
Question 4.101
- (a) Which of the vector fields in Exercises 13–16 could be gradient fields?
- (b) Which of the vector fields in Exercises 9–12 could be the curl of some vector field \(\textbf{V} \colon \mathbb R^3 \to \mathbb R^3\)?
Question 4.102
Let \(\textbf{F}(x, y, z)=(e^{xz}, \sin(xy), x^5y^3z^2)\).
- (a) Find the divergence of \(\textbf{F}\).
- (b) Find the curl of \(\textbf{F}\).
Question 4.103
Suppose \(f\colon \mathbb R^3 \to \mathbb R\) is a \(C^2\) scalar function. Which of the following expressions are meaningful, and which are nonsense? For those which are meaningful, decide whether the expression defines a scalar function or a vector field.
- (a) curl(grad\(f\))
- (b) grad(curl \(f\)))
- (c) div(grad \(f\))
- (d) grad(div \(f\))
- (e) curl (div \(f\))
- (f) div(curl \(f\))
Question 4.104
Suppose \(\textbf{F}\colon \mathbb R^3 \to \mathbb R^3\) is a \(C^2\) vector field. Which of the following expressions are meaningful, and which are nonsense? For those which are meaningful, decide whether the expression defines a scalar function or a vector field.
- (a) curl(grad \(\textbf{F}\))
- (b) grad(curl \(\textbf{F}\)))
- (c) div(grad \(\textbf{F}\))
- (d) grad(div \(\textbf{F}\))
- (e) curl (div \(\textbf{F}\))
- (f) div(curl \(\textbf{F}\))
Question 4.105
Suppose \(f, g, h \colon \mathbb R \to \mathbb R\) are differentiable. Show that the vector field \(\textbf{F}(x, y, z)= \big( f(x), g(y), h(z) \big)\) is irrotational.
Question 4.106
Suppose \(f, g, h \colon \mathbb R^2 \to \mathbb R\) are differentiable. Show that the vector field \(\textbf{F}(x, y, z)= \big( f(y, z), g(x, z), h(x, y) \big)\) has zero divergence.
Question 4.107
Prove identity 13 in the list of vector identities.
Verify that \(\nabla \times (\nabla f)={\bf 0}\) for the functions in Exercises 29 to 32.
Question 4.108
\(f(x,y,z)=\sqrt{x^2+y^2+z^2}\)
Question 4.109
\(f(x,y,z)=xy+yz+xz\)
Question 4.110
\(f(x,y,z)=1/(x^2+y^2+z^2)\)
Question 4.111
\(f(x,y,z)=x^2y^2+y^2z^2\)
Question 4.112
Show that \({\bf F}=y(\cos x){\bf i}+x(\sin y){\bf j}\) is not a gradient vector field.
Question 4.113
Show that \({\bf F}=(x^2+y^2){\bf i}-2xy{\bf j}\) is not a gradient field.
260
Question 4.114
Prove identity 10 in the list of vector identities.
Question 4.115
Suppose that \(\nabla \,{\cdot}\, {\bf F}= 0\) and \(\nabla \,{\cdot}\, {\bf G}=0\). Which of the following necessarily have zero divergence?
- (a) \({\bf F}+{\bf G}\)
- (b) \({\bf F}\times {\bf G}\)
Question 4.116
Let \({\bf F}=2xz^2{\bf i}+{\bf j}+y^3 zx{\bf k}\) and \(f=x^2y\). Compute the following quantities.
- (a) \(\nabla f\)
- (b) \(\nabla \times {\bf F}\)
- (c) \({\bf F}\times \nabla f\)
- (d) \({\bf F} \,{\cdot}\, (\nabla f)\)
Question 4.117
Let \({\bf r}(x,y,z)=(x,y,z)\) and \(r=\sqrt{x^2+y^2+z^2}=\|{\bf r}\|\). Prove the following identities.
- (a) \(\nabla (1/r)=-{\bf r}/r^3,r\neq 0\); and, in general, \(\nabla (r^n)=nr^{n-2}{\bf r}\) and \(\nabla (\log r)={\bf r}/r^2\).
- (b) \(\nabla^2 (1/r)=0,r\neq 0;\) and, in general, \(\nabla^2 r^n=n(n+1)\,r^{n-2}.\)
- (c) \(\nabla \,{\cdot}\, ({\bf r}/r^3)=0;\) and, in general, \(\nabla \,{\cdot}\, (r^n {\bf r})=(n+3)\,r^n\).
- (d) \(\nabla \times {\bf r} = {\bf 0};\) and, in general, \(\nabla \times (r^n {\bf r})={\bf 0}\).
Question 4.118
Does \(\nabla \times {\bf F}\) have to be perpendicular to \({\bf F}\)?
Question 4.119
Let \({\bf F}(x,y,z)=3 x^2 y{\bf i}+(x^3+y^3){\bf j}\).
- (a) Verify that curl \({\bf F}={\bf 0}\).
- (b) Find a function \(f\) such that \({\bf F}=\nabla f\). (Techniques for constructing \(f\) in general are given in Chapter 8. The one in this problem should be sought by trial and error.)
Question 4.120
Show that the real and imaginary parts of each of the following complex functions form the components of an irrotational and incompressible vector field in the plane; here \(i=\sqrt{-1}.\)
- (a) \((x-iy)^2\)
- (b) \((x-iy)^3\)
- (c) \(e^{x-iy}=e^x(\cos y-i\sin y)\)