Exercises for Section 14.6
In Exercises 1 to 8, sketch the given vector field or a small multiple of it.
Question 14.169
\({\bf F}(x,y)=(2,2)\)
Question 14.170
\({\bf F}(x,y)=(4,0)\)
Question 14.171
\({\bf F}(x,y)=(x,y)\)
Question 14.172
\({\bf F}(x,y)=(-x,y)\)
Question 14.173
\({\bf F}(x,y)=(2y,x)\)
Question 14.174
\({\bf F}(x,y)=(y,-2x)\)
Question 14.175
\({\bf F}(x,y)=\bigg(\displaystyle\frac{x}{\sqrt{x^2+y^2}},\displaystyle\frac{y}{\sqrt{x^2+y^2}}\bigg)\)
Question 14.176
\({\bf F}(x,y)=\bigg(\displaystyle\frac{y}{\sqrt{x^2+y^2}},\displaystyle\frac{x}{\sqrt{x^2+y^2}}\bigg)\)
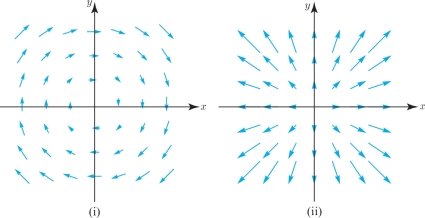
In the following two exercises, match the given vector field with its pictorial description (see Figure # and Figure #).
Question 14.177
- (a) \(\textbf{V}(x,y) = x \textbf{i} + y \textbf{j}\)
- (b) \(\textbf{V}(x,y) = y \textbf{i} - x \textbf{j}\)
Question 14.178
- (a) \(\textbf{V}(x,y) = \displaystyle\frac{y}{\sqrt{x^2 + y^2}} \textbf{i} - \displaystyle\frac{x}{\sqrt{x^2 + y^2}} \textbf{j}\)
- (b) \(\textbf{V}(x,y) = \displaystyle\frac{x}{\sqrt{x^2 + y^2}} \textbf{i} + \displaystyle\frac{y}{\sqrt{x^2 + y^2}} \textbf{j}\)
Where are these vector fields not defined? How are these vector fields related to those in Problem 9?

In Exercises 11 to 14, sketch a few flow lines of the given vector field.
Question 14.179
\({\bf F}(x,y)=(y,-x)\)
Question 14.180
\({\bf F}(x,y)=(x,-y)\)
Question 14.181
\({\bf F}(x,y)=(x,x^2)\)
Question 14.182
\({\bf F}(x,y,z)=(y,-x,0)\)
244
In Exercises 15 to 18, show that the given curve \({\bf c}(t)\) is a flow line of the given velocity vector field \({\bf F}(x,y,z)\).
Question 14.183
\({\bf c}(t)=(e^{2t},\log |t|,1/t),t\neq 0; {\bf F}(x,y,z)=(2x,z,-z^2)\)
Question 14.184
\({\bf c}(t)=(t^2,2t-1,\sqrt{t}),t > 0 ;{\bf F}(x,y,z)=(y+1,2,1/2z)\)
Question 14.185
\({\bf c}(t)=(\sin t,\,\cos t,e^t);{\bf F}(x,y,z)=(y,-x,z)\)
Question 14.186
\({\bf c}(t)=(\displaystyle\frac{1}{t^3},e^t,\displaystyle\frac{1}{t});{\bf F}(x,y,z)=(-3z^4,y,-z^2)\)
Question 14.187
Let \(\textbf{F}(x,y,z)=(x^2,yx^2,z+zx)\) and \(\textbf{c}(t)= (\displaystyle\frac{1}{1-t},0,\displaystyle\frac{e^t}{1-t})\). Show \(\textbf{c}(t)\) is a flow line for \(\textbf{F}\).
Question 14.188
Show that \(\textbf{c}(t)=(a\cos t-b \sin t, a \sin t +b\cos t)\) is a flow line for \(\textbf{F}(x, y)=(-y, x)\) for all real values of \(a\) and \(b\).
Question 14.189
- (a) Let \(\textbf{F}(x, y, z)= (yz, xz, xy)\). Find a function \(f \colon \mathbb R^3 \to \mathbb R\) such that \(\textbf{F}=\nabla f\).
- (b) Let \(\textbf{F}(x, y, z)= (x, y, z)\). Find a function \(f \colon \mathbb R^3 \to \mathbb R\) such that \(\textbf{F}=\nabla f\).
Question 14.190
Let \(f(x, y)=x^2+y^2\). Sketch the gradient vector field \(\nabla f\) together with some level sets of \(f\). How are they related?
Question 14.191
Show that it takes half as much energy to launch a satellite into an orbit just above the earth as it does to escape the earth. (Ignore the rotation of the earth.)
Question 14.192
Let \({\bf c}(t)\) be a flow line of a gradient field \({\bf F}=-{\nabla} V\). Prove that \(V({\bf c}(t))\) is a decreasing function of \(t\).
Question 14.193
Suppose that the isotherms in a region are all concentric spheres centered at the origin. Prove that the energy flux vector field points either toward or away from the origin.
Question 14.194
Sketch the gradient field \(-{ \nabla} V\) for \(V(x,y)=(x+y)/(x^2+y^2)\) and the equipotential surface \(V=1\).
Question 14.195
Let \(\textbf{F}(x, y, z)= (xe^y, y^2z^2, xyz)\) and suppose \(\textbf{c}(t)=\big(x(t), y(t), z(t)\big)\) is a flow line for \(\textbf{F}\). Find the system of differential equations that the functions \(x(t), y(t),\) and \(z(t)\) must satisfy.