14.7 The Divergence and Curl of a Vector Field
245
For each of the divergence and curl operations, we will make use of the del operator, defined by \[ \nabla = {\bf i} \frac{\partial}{\partial x}+ {\bf j} \frac{\partial}{\partial y}+ {\bf k} \frac{\partial}{\partial z}. \]
In \(n\)-space \[ \nabla = \bigg(\frac{\partial}{\partial x_1}, \frac{\partial}{\partial x_2}, \cdots, \frac{\partial}{\partial x_n}\bigg). \]
For functions of one variable, taking a derivative can be thought of as an operation or process; that is, given a function \(y = f(x) \), its derivative is the result of operating on \(y\) by the derivative operator \(d/{\it dx}\). Similarly, we can write the gradient as \[ \nabla f = \bigg( {\bf i} \frac{\partial}{\partial x}+ {\bf j} \frac{\partial}{\partial y} \bigg)f = {\bf i} \frac{\partial f}{\partial x}+ {\bf j} \frac{\partial f}{\partial y} \] for functions of two variables, and \[ \nabla f = \bigg( {\bf i} \frac{\partial}{\partial x} + {\bf j} \frac{\partial}{\partial y} + {\bf k} \frac{\partial}{\partial z} \bigg) f = {\bf i} \frac{\partial f}{\partial x} + {\bf j} \frac{\partial f}{\partial y} + {\bf k} \frac{\partial f}{\partial z} \] for three variables. In operational terms, the gradient of \(f\) is obtained by taking the \(\nabla\) operator and applying it to \(f\).
Definition of Divergence
We define the divergence of a vector field \({\bf F}\) by taking the dot product of \(\nabla\) with \({\bf F}\).
Divergence
If \({\bf F} = F_1 {\bf i} + F_2 {\bf j}+ F_3 {\bf k}\), the divergence of \({\bf F}\) is the scalar field \[ \hbox{div } {\bf F} = \nabla\, {\cdot}\, {\bf F}= \frac{\partial F_1}{\partial x} + \frac{\partial F_2}{\partial y}+ \frac{\partial F_3}{\partial z}. \]
Similarly, if \({\bf F} = ( F_1, \ldots , F_n)\) is a vector field on \({\mathbb R}^n\), its divergence is \[ \mbox{div } {\bf F} = \sum_{i=1}^n \frac{\partial F_i}{\partial x_i}=\frac{\partial F_1}{\partial x_1}+\frac{\partial F_2}{\partial x_2}+\cdots +\frac{\partial F_n}{\partial x_n}. \]
example 1
Compute the divergence of \[ {\bf F} = x^2 y {\bf i} + z {\bf j} + xy z {\bf k}. \]
solution \[ \hbox{div } {\bf F} = \frac{\partial}{\partial x} ( x^ 2 y) + \frac{\partial}{\partial y} (z) + \frac{\partial}{\partial z} (xyz)=2 xy + 0 + xy = 3xy \]
Question 14.196 Section 14.7 Progress Check Question 1
Compute the divergence of \[ {\bf F} = xyz^2 {\bf i} + xy^2 {\bf j} - xyz {\bf k}. \]
| A. |
| B. |
| C. |
| D. |
| E. |
246
Interpretation
The divergence has an important physical interpretation. If we imagine \({\bf F}\) to be the velocity field of a gas (or a fluid), then div \({\bf F}\) represents the rate of expansion per unit volume under the flow of the gas (or fluid). If div \({\bf F}\,{<}\,0\), the gas (or fluid) is compressing. For a vector field \({\bf F}(x, y)=F_{1} {\bf i} + F_{2}{\bf j}\) on the plane, the divergence \[ \nabla\,{\cdot}\,{\bf F}=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y} \] measures the rate of expansion of area.
This interpretation is explained graphically, as follows. Choose a small region \(W\) about a point \({\bf x}_{0}\). For each point \({\bf x}\) in \(W\), let \({\bf x}(t)\) be the flow line emanating from \({\bf x}\). The set of points \({\bf x}(t)\) describe how the set \(W\) flows after time \(t\) (see Figure 14.52).
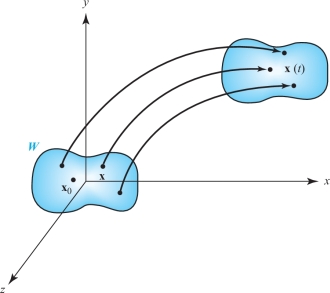
Call the region that results after time \(t\) has elapsed \(W(t)\), and let \({\cal V}(t)\) be its volume (or area in two dimensions). Then the relative rate of change of volume is the divergence; more precisely, \[ \frac{1}{{\cal V}(0)}\frac{d}{{\it dt}}{\cal V}(t)\bigg|_{t=0}\,{\approx}\, \hbox{ div } {\bf F}({\bf x}_0), \] with the approximation being more exact as \(W\) shrinks to \({\bf x}_{0}\).
For further discussion and the direct proof of this interpretation of the divergence, click here.
\(\bf Flows \ of \ Vector \ Fields.\) It is convenient to give the unique solution through a given point at time \(0\) a special notation: \[ \phi (\mathbf{x}, t) = \left\{ \begin{array}{l}\mbox{the position of the point on the flow line}\\ \mbox{through the point \(\mathbf{x}\) after time \(t\) has elapsed}. \end{array} \right\}. \] With \(\mathbf{x}\) as the initial condition, follow along the flow line for a time period \(t\) until the new position \(\phi(\mathbf{x}, t)\) is reached (see the Figure below).
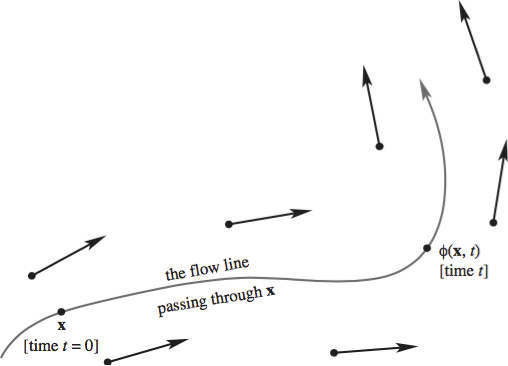
Alternatively, \(\phi (\mathbf{x}, t) \) is defined by: \begin{equation} \label {flowequation} \left.\begin{array}{c} \displaystyle{\frac{\partial }{\partial t}} \phi(\mathbf{x}, t) = \mathbf{F} (\phi(\mathbf{x}, t)) \\ \phi(\mathbf{x}, 0) = \mathbf{x} \end{array} \right\}.\tag{1} \end{equation} We call the mapping \(\phi\), which is regarded as the function of the variables \(\mathbf{x}\) and \(t\), the \({\bf flow}\) of \(\mathbf{F}\). Let \(\mathbf{D}_{\mathbf{x}}\) denote differentiation with respect to \(\mathbf{x}\), holding \(t\) fixed. It is proved in courses on differential equations that \(\phi\) is, in fact, a differentiable function of \(\mathbf{x}\). By differentiating equation (1) with respect to \(\mathbf{x}\), we get \[ \mathbf{D}_{\mathbf{x}} \frac{\partial }{\partial t} \phi(\mathbf{x}, t) = \mathbf{D}_{\mathbf{x}}[\mathbf{F}( \phi (\mathbf{x}, t))] . \] The equality of mixed partial derivatives may be used on the left-hand side of this equation and the chain rule applied to the right-hand side, yielding \begin{equation}\label{equation2} \frac{\partial }{\partial t}\mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t) = \mathbf{D}\mathbf{F}(\phi (\mathbf{x}, t))\mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t) ,\tag{2} \end{equation} where \(\mathbf{D}\mathbf{F}(\phi (\mathbf{x}, t))\) denotes the derivative of \(\mathbf{F}\) evaluated \( \phi(\mathbf{x}, t)\). Equation (2), a linear differential equation for \( \mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t)\) is called the {\bfi equation of the first variation}. It will be useful in our discussion of divergence in the next section. Both \(\mathbf{D}_{\mathbf{x}} \mathbf{F}(\phi)\) and \(\mathbf{D}_{\mathbf{x}} \phi \) are \(3 \times 3\) matrices since \(\mathbf{F}\) and \(\phi\) take values in \(\mathbb{R}^3\) and are differentiated with respect to \( \mathbf{x} \in \mathbb{R}^3\); for vector fields in the plane, they would be \(2 \times 2\) matrices.
\(\bf The \ Geometry \ of \ the \ Divergence.\) We now study the geometric meaning of the divergence in more detail. This discussion depends on the concept of the flow \(\phi (\mathbf{x}, t)\) of a vector field \(\mathbf{F}\) given in the preceding paragraph.
Fix a point \(\mathbf{x}\) and consider the three standard basis vectors \(\mathbf{i}, \mathbf{j}, \mathbf{k}\) emanating from \(\mathbf{x}\). Let \(\varepsilon \gt 0\) be small and consider the basis vectors \( \mathbf{v}_1 = \varepsilon \mathbf{i} , \mathbf{v}_2 = \varepsilon \mathbf{j}, \mathbf{v}_3 = \varepsilon \mathbf{k}\), also emanating from \(\mathbf{x}\). These vectors span a parallelepiped \(P(0)\). As time increases or decreases, the flow \(\phi(\mathbf{x}, t)\) carries \(P(0)\) into some object. For \({\it fixed}\) time, \(\phi\) is a differentiable function of \(\mathbf{x}\) (that is, \(\phi\) is a differentiable map of \(\mathbb{R}^3\) to \(\mathbb{R}^3\)). When \(\varepsilon \) is small, the image of \(P(0)\) under \(\phi\) can be approximated by its image under the derivative of \( \phi\) with respect to \(\mathbf{x}\). Recall that if \(\mathbf{v}\) is a vector based at a point \(P_1\) and ending at \(P_2\), so \(\mathbf{v} = P_2 - P_1\), then \(\phi(P_2, t) - \phi (P_1, t) \approx \mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t) \cdot \mathbf{v}\). Thus for fixed time and small positive \( \varepsilon, P(0)\) is approximately carried into a parallelepiped spanned by the vectors \( \mathbf{v}_1 (t), \mathbf{v}_2 (t), \mathbf{v}_3 (t)\) given by \begin{equation}\label{equation3} \left. \begin{array}{c} \mathbf{v}_1(t) = \mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t) \cdot \mathbf{v}_1\\ \mathbf{v}_2 (t) = \mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t) \cdot \mathbf{v}_2\\ \mathbf{v}_3 (t) = \mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t) \cdot \mathbf{v}_3 \end{array} \right\}.\tag{3} \end{equation} Since \(\phi( \mathbf{x}, 0) = \mathbf{x}\) for all \(\mathbf{x}\), it follows that \(\mathbf{v}_1(0) = \mathbf{v}_1, \mathbf{v}_2(0) = \mathbf{v}_2\), and \(\mathbf{v}_3(0) = \mathbf{v}_3\). In summary, the vectors \( \mathbf{v}_1 (t), \mathbf{v}_2(t), \mathbf{v}_3 (t)\) span a parallelepiped \(P(t) \) that moves in time (see the Figure below).
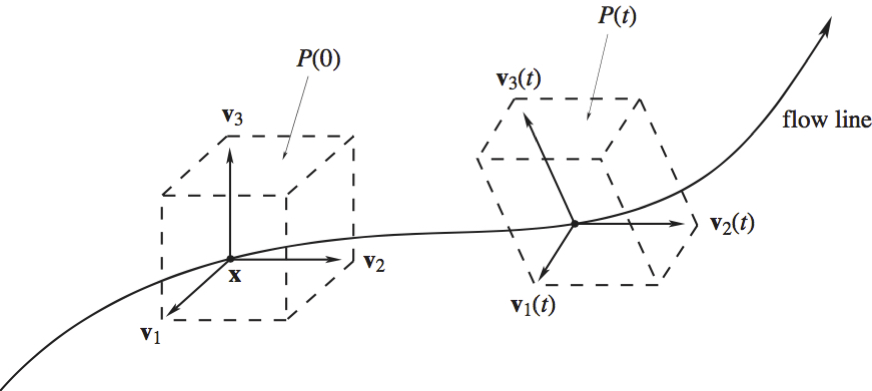
Let the volume of \(P(t)\) be denoted by \(\mathcal{V}(t)\). The main geometric meaning of divergence is given by the following theorem.
\({\bf Theorem.}\) \[\operatorname{div} \mathbf{F}(\mathbf{x}) \left. = \frac{1}{\mathcal{V}(0)} \frac{d}{dt} \mathcal{V} (t) \right|_{t = 0} .\]
\(\bf proof\) By equation (2) of the previous paragraph, \begin{equation}\label{equation4} \frac{d}{dt} \mathbf{v}_i (t) = \mathbf{D} \mathbf{F} (\phi(\mathbf{x}, t)) \cdot (\mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, t) \cdot \mathbf{v}_i)\tag{4} \end{equation} for \(i = 1, 2, 3\). Since \( \phi(\mathbf{x}, 0) = \mathbf{x}\), it follows that \(\mathbf{D}_{\mathbf{x}} \phi (\mathbf{x}, 0)\) is the identity matrix, so that evaluation at \(t=0\) gives \[ \left.\frac{d}{dt} \mathbf{v}_i (t) \right|_{t = 0} = \mathbf{D} \mathbf{F}(\mathbf{x}) \cdot \mathbf{v}_i. \] The volume \(\mathcal{V} (t)\) is given by the triple product: \[ \mathcal{V}(t) = \mathbf{v}_1 (t) \cdot [\mathbf{v}_2(t) \times \mathbf{v}_3(t)]. \] Using the differentiation rules of \S4.1 and the identities \[ \mathbf{v}_1 \cdot [\mathbf{v}_2 \times \mathbf{v}_3 ] = \mathbf{v}_2 \cdot[\mathbf{v}_3 \times \mathbf{v}_1] = \mathbf{v}_3 \cdot [ \mathbf{v}_1 \times \mathbf{v}_2], \] equation (\ref{equation4}) gives \begin{eqnarray*} \frac{d \mathcal{V}}{dt} &= &\frac{d \mathbf{v}_1}{dt} \cdot [ \mathbf{v}_2 (t) \times \mathbf{v}_3(t)] + \mathbf{v}_1 (t) \cdot \left[ \frac{d \mathbf{v}_2}{dt} \times \mathbf{v}_3(t)\right] + \mathbf{v}_1(t) \cdot \left[ \mathbf{v}_2 (t) \times \frac{d \mathbf{v}_3}{dt} \right]\\ & = & \frac{d \mathbf{v}_1}{dt} \cdot \left[ \mathbf{v}_2 (t) \times \mathbf{v}_3(t)] + \frac{d \mathbf{v}_2}{dt} \cdot [ \mathbf{v}_3 (t) \times \mathbf{v}_1(t) ] + \frac{d \mathbf{v}_3}{dt} \cdot [\mathbf{v}_1 (t) \times \mathbf{v}_2 (t)\right] . \end{eqnarray*} At \( t = 0\), substitution from formula (\ref{equation3}) and the facts that \[ \mathbf{v}_1 \times \mathbf{v}_2 = \varepsilon \mathbf{v}_3, \quad \mathbf{v}_3 \times \mathbf{v}_1 = \varepsilon \mathbf{v}_2 \quad \mbox{and} \quad \mathbf{v}_2 \times \mathbf{v}_3 = \varepsilon \mathbf{v}_1, \] gives \begin{equation}\label{equation5} \left.\frac{d \mathcal{V}}{dt}\right|_{t = 0} = \varepsilon ^3 [\mathbf{D} \mathbf{F} (\mathbf{x}) \mathbf{i}] \cdot \mathbf{i} + \varepsilon ^3 [\mathbf{D}\mathbf{F}(\mathbf{x})\mathbf{j}]\cdot \mathbf{j} + \varepsilon^3 [\mathbf{D}\mathbf{F}(\mathbf{x})\mathbf{k}]\cdot\mathbf{k}.\tag{5} \end{equation} Since \( \mathbf{F} = F_1 \mathbf{i} + F_2 \mathbf{j}+F_3 \mathbf{k}\), we get \([\mathbf{D}\mathbf{F}(\mathbf{x})\mathbf{i}]\cdot \mathbf{i} = \partial F_1/\partial x\). Similarly, the second and third terms of equation (\ref{equation5}) are \(\varepsilon^3(\partial F_2/\partial y)\) and \( \varepsilon ^3 (\partial F _3 / \partial z \)). Substituting these facts into equation (\ref{equation5}) and dividing by \(\mathcal{V}(0) = \varepsilon ^3\) proves the theorem. \( \Box\)
In addition to the direct proof of this, we give a more natural argument in Chapter 8, in the context of the integral theorems of vector calculus.
example 2
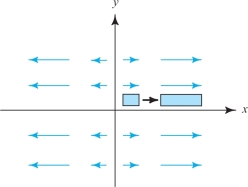
Consider the vector field in the plane given by \({\bf V} (x,y) = x {\bf i}\). Relate the sign of the divergence of \({\bf V}\) with the rate of change of areas under the flow.
solution We think of \({\bf V}\) as the velocity field of a fluid in the plane. The vector field \({\bf V}\) points to the right for \(x > 0\) and to the left if \(x < 0\), as we see in Figure 14.53. The length of \({\bf V}\) gets shorter toward the origin. As the fluid moves, it expands (the area of the shaded rectangle increases), so we expect div \({\bf V} > 0\). Indeed, div \({\bf V} =1\).
247
example 3
The flow lines of the vector field \({\bf F} = x {\bf i}+ y {\bf j}\) are straight lines directed away from the origin (Figure 14.54).
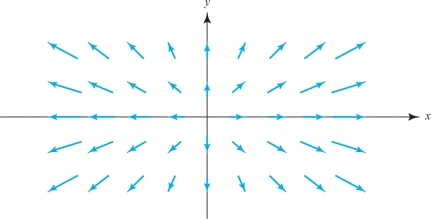
If these flow lines are those of a fluid, the fluid is expanding as it moves out from the origin, so div \({\bf F}\) should be positive. In fact, \[ \nabla \,{\cdot}\, {\bf F} = \frac{\partial}{\partial x} x+ \frac{\partial}{\partial y} y = 2 > 0. \]
example 4
Consider the vector field \({\bf F} = - x {\bf i} - y {\bf j}\). Here the flow lines point toward the origin instead of away from it (see Figure 14.55). Therefore, the fluid is compressing, so we expect \((\hbox{div }{\bf F}) < 0\). Calculating, we see that \[ \nabla \,{\cdot}\, {\bf F} = \frac{\partial}{\partial x} ( -x) + \frac{\partial}{\partial y} (-y) = -1 -1 = - 2 < 0. \]
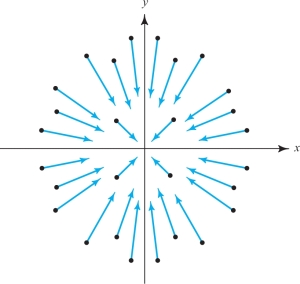
example 5
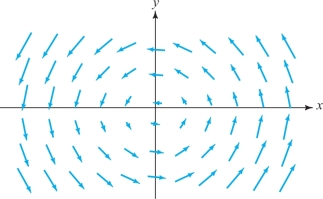
As we saw in the last section, the flow lines of \({\bf F}=-y {\bf i}+ x {\bf j}\) are concentric circles about the origin, moving counterclockwise (see Figure 14.56). From this figure, it appears that the fluid is neither compressing nor expanding. This is confirmed by calculating \[ \nabla \,{\cdot}\, {\bf F} = \frac{\partial}{\partial x} (-y) + \frac{\partial}{\partial y} (x) = 0 + 0 =0. \]
248
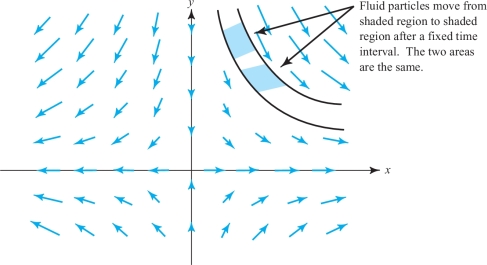
example 6
Some flow lines of \({\bf F} = x {\bf i} - y {\bf j}\) are shown in Figure 14.57. Here our intuition about expansion or compression is less clear. However, it is true that the shaded regions shown have the same area, and we calculate that \[ \nabla \,{\cdot}\, {\bf F}= \frac{\partial}{\partial x} x+ \frac{\partial}{\partial y} (-y)= 1+ (-1) =0. \]
Curl
249
To calculate the curl, the second basic operation performed on vector fields, we take the cross product of \(\nabla\) with \({\bf F}\).
Curl of a Vector Field
If \({\bf F} = F_1 {\bf i}+ F_2 {\bf j} + F_3 {\bf k}\), the curl of \({\bf F}\) is the vector field \begin{eqnarray*} \hbox{curl } {\bf F} = \nabla \times {\bf F} & = & \left|\begin{array}{ccc} \displaystyle {\bf i } & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\[7pt] F_1 & F_2 & F_3 \end{array} \right| \\[6pt] & = & \bigg( \frac{\partial F_3}{\partial y} - \frac{\partial F_2}{\partial z} \bigg) {\bf i}+ \bigg( \frac{\partial F_1}{\partial z} - \frac{\partial F_3}{\partial x} \bigg) {\bf j}+ \bigg( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \bigg) {\bf k.}\\[-18pt] \end{eqnarray*}
If we write \({\bf F} = P{\bf i}+Q{\bf j}+R{\bf k}\), which is alternative notation, the same formula for the curl reads \begin{eqnarray*} \hbox{curl } {\bf F} &=& \left|\begin{array}{ccc} \displaystyle {\bf i } & {\bf j} & {\bf k} \\ \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\[7pt] P & Q & R \end{array} \right| \\[6pt] & = & \bigg(\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}\bigg) {\bf i} - \bigg(\frac{\partial R}{\partial x} - \frac{\partial P}{\partial z}\bigg){\bf j}+ \bigg(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\bigg) {\bf k.} \end{eqnarray*}
example 7
Let \({\bf F} (x,y,z) = x {\bf i}+ xy {\bf j} + {\bf k}\). Find \(\nabla \times {\bf F}.\)
solution We use the preceding formula: \[ \nabla \times {\bf F} = \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial}{\partial x} & \displaystyle\frac{\partial}{\partial y} & \displaystyle\frac{\partial}{\partial z}\\[7pt] x & xy & 1 \end{array} \right|=(0-0){\bf i}-(0-0){\bf j}+(y-0){\bf k.} \]
Thus, \(\nabla \times {\bf F} = y {\bf k}.\)
example 8
Find the curl of \(xy {\bf i} - \sin z {\bf j} + {\bf k}\).
solution Letting \({\bf F} = xy {\bf i} -\sin z {\bf j} + {\bf k},\) \begin{eqnarray*} \nabla \times {\bf F} & = & \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\[7pt] xy& {-}{\sin z} & 1 \end{array} \right| \\[6pt] & = & \left| \begin{array}{cc} \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\[7pt] {-}{\sin z} & 1 \end{array} \right| {\bf i} - \left| \begin{array}{ccc} \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial z} \\[7pt] xy & 1 \end{array} \right| {\bf j} + \left| \begin{array}{ccc} \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} \\[7pt] xy & {-}{\sin z} \end{array} \right| {\bf k} \\[3pt] & = & \,\cos z {\bf i} - x {\bf k}. \\[-36pt] \end{eqnarray*}
Question 14.197 Section 14.7 Progress Check Question 2
Find the curl of \({\bf F} = x^2y {\bf i} +(y- z) {\bf j} + e^{xz} {\bf k}\).
| A. |
| B. |
| C. |
| D. |
| E. |
250
Unlike the divergence, which can be defined in \({\mathbb R}^n\) for any \(n\), we define the curl only in three-dimensional space (or for planar vector fields, regarding their third component as zero).
The Curl and Rotations
The physical significance of the curl will be discussed in Chapter 18, when we study Stokes' theorem. However, we can now consider a specific situation, in which the curl is associated with rotations.
example 9
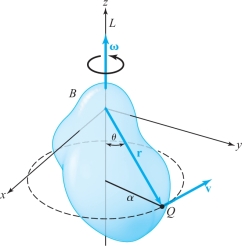
Consider a solid rigid body \(B\) rotating about an axis \(L\). The rotational motion of the body can be described by a vector \(\boldsymbol{\omega}\) along the axis of rotation, the direction being chosen so that the body rotates about \(\boldsymbol{\omega}\), as in Figure 14.58. We call \(\boldsymbol{\omega}\) the angular velocity vector. The length \(\,\omega = \|\boldsymbol{\omega} \|\) is taken to be the angular speed of the body \(B\); that is, the speed of any point in \(B\) divided by its distance from the axis \(L\) of rotation. The motion of points in the rotating body is described by the vector field \({\bf v}\) whose value at each point is the velocity at that point. To find \({\bf v}\), let Q be any point in \(B\) and let \(\,\alpha\) be the distance from Q to \(L\).
Figure 14.58 shows that \(\,\alpha = \|{\bf r} \|\,\sin\,\theta\), where \({\bf r}\) is the vector whose initial point is the origin and whose terminal point is Q and \(\,\theta\) is the angle between \({\bf r}\) and the axis \(L\) of rotation. The tangential velocity \({\bf v}\) of Q is directed counterclockwise along the tangent to a circle parallel to the \(xy\) plane with radius \(\,\alpha\) and has magnitude \[ \|{\bf v} \| = \,\omega \,\alpha = \,\omega \|{\bf r} \|\,\sin \,\theta = \|\boldsymbol{\omega}\| \|{\bf r} \| \,\sin \,\theta. \]
The direction and magnitude of \({\bf v}\) imply that \({\bf v} = \boldsymbol{\omega} \times {\bf r}\). Selecting a coordinate system in which \(L\) is the \(z\) axis, we can write \(\boldsymbol{\omega} = \,\omega {\bf k}\) and \({\bf r} = x {\bf i} + y {\bf j}+ z {\bf k}\). Thus, \[ {\bf v} = \boldsymbol{\omega} \times {\bf r} = - \,\omega y {\bf i} + \,\omega x {\bf j}, \] and so \[ \hbox{curl } {\bf v} = \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\[7pt] -\omega y & \,\omega x & 0 \end{array} \right| = 2 \,\omega {\bf k} = 2\boldsymbol{\omega}. \]
Hence, for the rotation of a rigid body, the curl of the velocity vector field is a vector field whose value is the same at each point. It is directed along the axis of rotation with magnitude twice the angular speed.
The Curl and Rotational Flow
251
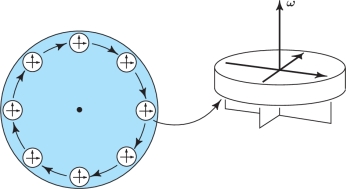
If a vector field represents the flow of a fluid, then the value of \(\nabla \times {\bf F}\) at a point is twice the angular velocity vector of a rigid body that rotates as the fluid does near that point. In particular, \(\nabla \times {\bf F} = {\bf 0}\) at a point P means that the fluid is free from rigid rotations at \(P\); that is, it has no whirlpools. Another justification of this idea depends on Stokes' theorem from Chapter 8. However, we can say informally that curl \({\bf F} = {\bf 0}\) means that if a small rigid paddle wheel is placed in the fluid, it will move with the fluid but will not rotate around its own axis. Such a vector field is called irrotational. For example, it has been determined from experiments that fluid draining from a tub is usually irrotational except right at the center, even though the fluid is “rotating” around the drain (see Figure 14.59). In Example 10, the flow lines of the vector field \({\bf V}\) are circles about the origin, yet we show that the flow is irrotational. Thus, the reader should be warned of the possible confusion the word “irrotational” can cause.
example 10
Verify that the vector field \[ {\bf V} (x,y,z) = \frac{y {\bf i} - x {\bf j}}{x^2 + y^2} \] is irrotational when \((x,y) \ne (0,0)\) (i.e., except where \({\bf V}\) is not defined).
solution The curl is \begin{eqnarray*} \nabla \times {\bf V} & = & \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\[12pt] \displaystyle\frac{y}{x^2 + y^2} & \displaystyle\frac{-x}{x^2 + y^2} & 0 \end{array} \right| \\[10pt] & = & 0 {\bf i} + 0 {\bf j} + \bigg[ \frac{\partial}{\partial x} \bigg( \frac{-x}{x^2 + y^2} \bigg) - \frac{\partial}{\partial y} \bigg( \frac{y}{x^2 + y^2} \bigg) \bigg] {\bf k} \\[15pt] & = & \bigg[ \frac{- (x^2 + y^2) + 2 x^2}{(x^2 + y^2)^2}+ \frac{- (x^2 + y^2) + 2 y^2}{(x^2 + y^2)^2} \bigg] {\bf k} = {\bf 0}. \\[-30pt] \end{eqnarray*}
Gradients Are Curl Free
252
The following identity is a basic relation between the gradient and curl, which should be compared with the fact that for any vector \({\bf v}\), we have \({\bf v}\times {\bf v}={\bf 0}\).
Theorem 1 Curl of a Gradient
For any \(C^2\) function \(f\), \[ \nabla \times ( \nabla f) = {\bf 0}. \]
That is, the curl of any gradient is the zero vector.
proof
Because \(\nabla f = ( \partial f / \partial x , \partial f / \partial y, \partial f / \partial z)\) we have, by definition, \begin{eqnarray*} \nabla \times \nabla f & = & \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z}\\[9pt] \displaystyle \frac{\partial f}{\partial x} & \displaystyle \frac{\partial f}{\partial y} & \displaystyle \frac{\partial f}{\partial z} \end{array} \right| \\[12pt] & = & \bigg( \frac{\partial^2 f}{\partial y \,\partial z} -\frac{\partial^2 f}{\partial z\, \partial y} \bigg) {\bf i} + \bigg( \frac{\partial^2 f}{\partial z \,\partial x} -\frac{\partial^2 f}{\partial x \,\partial z} \bigg) {\bf j}+ \bigg( \frac{\partial^2 f}{\partial x\, \partial y} -\frac{\partial^2 f}{\partial y \,\partial x} \bigg) {\bf k}. \end{eqnarray*}
Each component is zero because of the equality of mixed partial derivatives.
The converse to this theorem (a vector field with zero curl is a gradient, under suitable hypotheses) will be discussed in Chapter 8.
example 11
Let \({\bf V} (x,y,z) = y {\bf i} - x {\bf j}\). Show that \({\bf V}\) is not a gradient field.
solution If \({\bf V}\) were a gradient field, then it would satisfy curl \({\bf V} ={\bf 0}\) by Theorem 1. But \[ \hbox{curl } {\bf V} = \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial }{\partial x} & \displaystyle \frac{\partial }{\partial y} & \displaystyle \frac{\partial }{\partial z} \\[7pt] y & - x & 0 \end{array} \right| = -2 {\bf k} \ne {\bf 0}, \] so \({\bf V}\) cannot be a gradient.
Scalar Curl
There is an operation on vector fields in the plane that is closely related to the curl. If \({\bf F} = P (x,y) {\bf i} + Q( x,y) {\bf j}\) is a vector field in the plane, it can also be regarded as a vector field in space for which the \({\bf k}\) component is zero and the other two components are independent of \(z\). The curl of \({\bf F}\) then reduces to \[ \nabla \times {\bf F} = \bigg( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \bigg) {\bf k} \] and always points in the \({\bf k}\) direction. The function \[ \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \] of \(x\) and \(y\) is called the scalar curl of \({\bf F}\).
253
example 12
Find the scalar curl of \({\bf V} (x,y) = - y^2 {\bf i} + x {\bf j}\).
solution The curl is \[ \nabla \times {\bf V} = \left| \begin{array}{ccc} {\bf i} & {\bf j} & {\bf k} \\[2pt] \displaystyle \frac{\partial}{\partial x} &\displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\[7pt] - y^2 & x & 0 \end{array} \right| = (1+2y)\, {\bf k}, \] so the scalar curl, which is the coefficient of \({\bf k}\), is \(1 + 2y\).
Question 14.198 Section 14.7 Progress Check Question 3
Find the scalar curl of \({\bf V} (x,y) = xy {\bf i} -y {\bf j}\).
| A. |
| B. |
| C. |
| D. |
| E. |
Curls Are Divergence Free
A basic relation between the divergence and curl operations is given next.
Theorem 2 Divergence of a Curl
For any \(C^2\) vector field \({\bf F},\) \[ \hbox{div } \hbox{curl } {\bf F} = \nabla \,{\cdot}\, ( \nabla \times {\bf F}) =0. \]
That is, the divergence of any curl is zero.
As with the curl of a gradient, the proof rests on the equality of the mixed partial derivatives. You should write out the details. A converse will be discussed in Chapter 8.
example 13
Show that the vector field \({\bf V} (x,y,z) = x {\bf i}+ y {\bf j} +z {\bf k}\) cannot be the curl of some vector field \({\bf F}\); that is, there is no \({\bf F}\) with \({\bf V} = \hbox{curl } {\bf F}\).
solution If this were so, then div \({\bf V}\) would be zero by Theorem 2. But \[ \hbox{div } {\bf V} = \frac{\partial x}{\partial x} + \frac{\partial y}{\partial y}+ \frac{\partial z}{\partial z} = 3 \ne 0, \] so \({\bf V}\) cannot be curl \({\bf F}\) for any \({\bf F}\).
Laplacian
254
The Laplace operator \(\nabla^2\), which operates on functions \(f\), is defined to be the divergence of the gradient: \[ \nabla^2 f = \nabla\, {\cdot}\, (\nabla f)=\frac{\partial^2 f}{\partial x^2}+ \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}. \]
This operator plays an important role in many physical laws, as we have mentioned in Section 14.1.
The next example is important in mathematical physics.
example 14
Show that \(\nabla^2 f =0\) for \[ f (x,y,z) = \frac{1}{\sqrt{x^2 + y^2 + z^2}} = \frac{1}{r} \hbox{and} \qquad (x,y,z) \ne (0,0,0), \] where \({\bf r} = x {\bf i} + y {\bf j}+ z {\bf k}\) and \(r = \| {\bf r} \|\).
solution The first derivatives are \[ \frac{\partial f}{\partial x}= \frac{-x}{(x^2 + y^2 + z^2)^{3/2}},\quad \frac{\partial f}{\partial y}= \frac{-y}{(x^2 + y^2 + z^2)^{3/2}},\quad \frac{\partial f}{\partial z}= \frac{-z}{(x^2 + y^2 + z^2)^{3/2}}. \]
Computing the second derivatives, we find that \begin{eqnarray*} \frac{\partial^2 f}{\partial x^2} & = & \frac{3 x^2}{(x^2 + y^2 +z^2)^{5/2}} - \frac{1}{(x^2 + y^2 + z^2)^{3/2}} , \\[9pt] \frac{\partial^2 f}{\partial y^2} & = & \frac{3 y^2}{(x^2 + y^2 +z^2)^{5/2}} - \frac{1}{(x^2 + y^2 + z^2)^{3/2}} , \\[9pt] \frac{\partial^2 f}{\partial z^2} & = & \frac{3 z^2}{(x^2 + y^2 +z^2)^{5/2}} - \frac{1}{(x^2 + y^2 + z^2)^{3/2}} . \end{eqnarray*}
Thus, \begin{eqnarray*} \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}+ \frac{\partial^2 f}{\partial z^2} & = & \frac{3 (x^2 + y^2 + z^2)}{(x^2 + y^2 + z^2)^{5/2}} - \frac{3}{(x^2 + y^2 + z^2)^{3/2}} \\[9pt] & = & \frac{3}{(x^2 + y^2 + z^2)^{3/2}} - \frac{3}{(x^2 + y^2 + z^2)^{3/2}}=0.\\[-30pt] \end{eqnarray*}
Vector Identities
We now have these basic operations on hand: gradient, divergence, curl, and the Laplace operator. The following box contains some basic general formulas that are useful when computing with vector fields.
255
Basic Identities of Vector Analysis
- \(\nabla ( f+ g) = \nabla f + \nabla g\)
- \(\nabla (cf) =c \nabla f\), for a constant \(c\)
- \(\nabla (fg) = f \nabla g + g \nabla f\)
- \(\nabla (f/g) = (g \nabla f- f\nabla g) / g^2\), at points \({\bf x}\) where \(g ({\bf x}) \ne 0\)
- \(\hbox{div } ({\bf F} + {\bf G}) = \hbox{div } {\bf F} + \hbox{div } {\bf G}\)
- \(\hbox{curl } ({\bf F} + {\bf G}) = \hbox{curl } {\bf F} + \hbox{curl } {\bf G}\)
- \(\hbox{div } ( f {\bf F}) = f \hbox{div } {\bf F} + {\bf F} \, {\cdot}\, \nabla f\)
- \(\hbox{div } ( {\bf F} \times {\bf G}) = {\bf G}\,{\cdot}\, \hbox{curl } {\bf F} - {\bf F} \,{\cdot}\, \hbox{curl } {\bf G}\)
- \(\hbox{div } \hbox{curl } {\bf F} =0\)
- \(\hbox{curl } ( f {\bf F}) = f \hbox{curl } {\bf F} + \nabla f \times {\bf F}\)
- \(\hbox{curl } \nabla f = {\bf 0}\)
- \(\nabla^2 (fg) = f\nabla^2 g + g \nabla^2 f + 2 ( \nabla f \,{\cdot}\, \nabla g)\)
- \(\hbox{div } ( \nabla f \times \nabla g) =0\)
- \(\hbox{div } ( f\nabla g - g \nabla f) = f \nabla^2 g -g \nabla^2 f\)
example 15
Prove identity 7 in the preceding box.
solution The vector field \(f {\bf F}\) has components \(f F_i,\) for \(i =1,2,3\), and so \[ \hbox{div } ( f{\bf F}) = \frac{\partial}{\partial x} (f F_1) + \frac{\partial}{\partial y} ( f F_2) + \frac{\partial}{\partial z} ( f F_3). \]
However, \((\partial / \partial x)(f F_1) = f \partial F_1 / \partial x + F_1 \partial f / \partial x\) by the product rule, with similar expressions for the other terms. Therefore, \begin{eqnarray*} \hbox{div } ( f {\bf F}) & = & f \bigg( \frac{\partial F_1}{\partial x}+ \frac{\partial F_2}{\partial y} + \frac{\partial F_3}{\partial z} \bigg)+ F_1 \frac{\partial f}{\partial x} + F_2 \frac{\partial f}{\partial y} + F_3 \frac{\partial f}{\partial z} \\[9pt] & = & f ( \nabla \,{\cdot}\, {\bf F}) + {\bf F} \,{\cdot}\, \nabla f. \\[-30pt] \end{eqnarray*}
Let us use these identities to redo Example 14.
256
example 16
Show that for \({\bf r} \ne {\bf 0}, \nabla^2 ( 1/ r) =0\).
solution As in the case of the gravitational potential, \(\nabla (1/ r) = -{\bf r} / r^3\). In general, \(\nabla (r^n)=nr^{n-2}{\bf r}\) (see Exercise 38). By the identity \(\nabla \,{\cdot}\, ( f {\bf F}) = f\nabla \,{\cdot}\, {\bf F}+\nabla f \,{\cdot}\, {\bf F}\), we get \begin{eqnarray*} \nabla \,{\cdot}\, \bigg(\frac{{\bf r}}{r^3} \bigg) & = & \frac{1}{r^3} \nabla \,{\cdot}\, {\bf r} + {\bf r} \,{\cdot}\, \nabla \bigg( \frac{1}{r^3} \bigg) \\[1.5pt] & = & \frac{3}{r^3} + {\bf r} \,{\cdot}\, \bigg( \frac{-3 {\bf r}}{r^5}\bigg) = \frac{3}{r^3}-\frac{3}{r^3} =0.\\[-36pt] \end{eqnarray*}
Historical Note
Divergence and Curl
William Rowan Hamilton, in his investigation of quaternions (discussed in Section 11.3), introduced the del operator, defined formally as \[ \nabla=\frac{\partial}{\partial x}{\bf i} + \frac{\partial}{\partial y}\,{\bf j}+ \frac{\partial}{\partial z}{\bf k}. \]
Hamilton firmly believed in the significance of this operator. If \(f(x, y, z)\) is a scalar function on \({\mathbb R}^{3}\), then “multiplication” by \(\nabla\) gives the gradient of \(f\): \[ \nabla f=\frac{\partial f}{\partial x}{\bf i} + \frac{\partial f}{\partial y}\,{\bf j}+ \frac{\partial f}{\partial z}{\bf k}\hbox{,} \] which, of course, gives the direction of steepest ascent (see Section #). If \[ {\bf V}\hbox{(}x\hbox{,} y\hbox{,} z\hbox{)}=V_{1}\hbox{(}x\hbox{,} y\hbox{,} z\hbox{)} {\bf i} + V_{2}\hbox{(}x\hbox{,} y\hbox{,} z\hbox{)} {\bf j} + V_{3}\hbox{(}x\hbox{,} y\hbox{,} z\hbox{)}{\bf k} \] is a vector field, then the “quaternionic multiplication” of \(\nabla\) with \({\bf V}\) yields \[ \nabla {\bf V} = -\hbox{div } {\bf V} \,{+}\, \hbox{curl } {\bf V}. \]
Thus, what we now call the divergence of \({\bf V}\) is the negative of the scalar part of this product, and curl \({\bf V}\) is the vector part (c.f. the quaternion discussion in Section 11.3).
As far as we are aware, Hamilton never gave a physical interpretation of divergence and curl, but he surely believed that, as a consequence of his faith in them, they must have an important physical interpretation. His faith in his mathematical formalism was justified, but a physical explanation of divergence and curl had to wait for James Clerk Maxwell’s Treatise on Electricity and Magnetism. Here, Maxwell used both the divergence and the curl in his equations for the interaction of electric and magnetic fields (the Maxwell equations are discussed in Chapter 18).
Curiously, Maxwell referred to divergence as convergence and to curl as rotation, a term still used in scientific research. It was Josiah Gibbs (Figure ) who renamed convergence and rotation as the more familiar terms we use today—divergence and curl.

Maxwell gave a physical interpretation of the divergence using the Gauss divergence theorem, as we do in Section 18.4. His physical interpretation of the curl as a rotation was rather brief. Gibbs provided a more elementary interpretation of divergence, as we do in this section. In the spirit of Leibniz (who believed in infinitesimal quantities \({\it dx}\hbox{,} {\it dy}\hbox{,} {\it dz}\)), Gibbs imagined placing a small cube of dimensions \({\it dx}\) by \({\it dy}\) by \({\it dz}\) in a fluid. The faces of this cube have areas \({\it dx}\, {\it dy}\hbox{,}\) \({\it dy}\, {\it dz}\), and \({\it dx}\, {\it dz}\).
Historical Note
257
At this point, you may be interested to hear Gibbs through the words of his student E. B. Wilson:
Consider the amount of fluid which passes through those faces of the cube which are parallel to the \({\it yz}\) plane, i.e., perpendicular to the \({\it x}\) axis [see Figure 14.61].
The normal to the face whose \(x\) coordinate is the lesser, that is, the normal to the left-hand face of the cube is –\({\bf i}\). The flux of substance through this face is \[ -{\bf i} \,{\cdot}\, {\bf V} \hbox{(}x\hbox{,}\, y\hbox{,}\, z\hbox{)} \, {{\it dy}\, {\it dz}.} \]
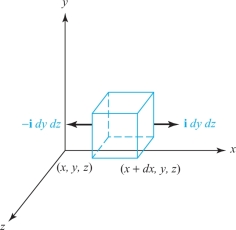
The normal to the opposite face, the face whose \(x\) coordinate is greater by the amount \({\it dx}\), is \({+}{\bf i}\), and the flux through it is therefore \begin{eqnarray*} \displaystyle {\bf i} \,{\cdot}\, {\bf V} \hbox{(}x + {\it dx}\hbox{,}\, y\hbox{,}\, z\hbox{)} \, {{\it dy}\, {\it dz}} &=& {\bf i} \,{\cdot}\, \bigg[{\bf V} (x\hbox{,}\, y\hbox{,}\, z\hbox{)} + \frac{\partial {\bf V}}{\partial x}\,{\it dx}\bigg] \ {{\it dy} \,{\it dz}}\\[1.5pt] \displaystyle &=& {\bf i} \,{\cdot}\, {\bf V} \hbox{(}x\hbox{,}\, y\hbox{,}\, z\hbox{)} \, {{\it dy} \, {\it dz} } + {\bf i} \,{\cdot}\,\frac{\partial {\bf V}}{\partial x} \ {{\it dx}\, {\it dy}\, {\it dz}.} \end{eqnarray*}
The total flux outward from the cube through these two faces is therefore the algebraic sum of these quantities. This is simply \[ {\bf i} \,{\cdot}\,\frac{\partial {\bf V}}{\partial x}\, {{\it dx}\, {\it dy}\, {\it dz} } = \frac{\partial {V}_1}{\partial x}\, {{\it dx}\, {\it dy}\, {\it dz}.} \]
In like manner the fluxes through the other pairs of faces of the cube are \[ {\bf j} \,{{\cdot}}\,\frac{\partial {\bf V}}{\partial y}\, {{\it dx}\, {\it dy}\, {\it dz} }\qquad\hbox{and } \qquad{\bf k} \,{{\cdot}}\,\frac{\partial {\bf V}}{\partial z}\,{{\it dx}\, {\it dy}\, {\it dz}.} \]
The total flux out from the cube is therefore \[ \bigg({\bf i}\,{{\cdot}}\,\frac{\partial {\bf V}}{\partial x}+ {\bf j}\,{{\cdot}}\,\frac{\partial {\bf V}}{\partial y}+ {\bf k}\,{{\cdot}}\,\frac{\partial {\bf V}}{\partial z}\bigg)\, {{\it dx}\, {\it dy}\, {\it dz}.} \]
This is the net quantity of fluid that leaves the cube per unit time. The quotient of this by the volume \({{\it dx}\, {\it dy}\, {\it dz}}\) of the cube gives the rate of diminution of density. This is \[ \nabla \,{\cdot}\, {\bf V} = {\bf i}\,{{\cdot}}\,\frac{\partial {\bf V}}{\partial x} + {\bf j}\,{{\cdot}}\,\frac{\partial {\bf V}}{\partial y} + {\bf k}\,{{\cdot}}\,\frac{\partial {\bf V}}{\partial z} = \frac{\partial {V}_1}{\partial x} + \frac{\partial {V}_2}{\partial y} + \frac{\partial {V}_3}{\partial z}. \]
258
Because \(\nabla\,{\cdot}\,{\bf V}\) thus represents the diminution of density or the rate at which matter is leaving a point per unit volume per unit time, it is called the divergence. Maxwell employed the term convergence to denote the rate at which fluid approaches a point per unit volume per unit time. This is the negative of the divergence. In the case that the fluid is incompressible, as much matter must leave the cube as enters it. The total change of contents must therefore be zero. For this reason, the characteristic differential equation that any incompressible fluid must satisfy is \[ \nabla \,{\cdot}\, {\bf V} = \hbox{0}, \] where \({\bf V}\) is the velocity of the fluid. This equation is often known as the hydrodynamic equation. It is satisfied by any flow of water, since water is practically incompressible. The great importance of the equation for work in electricity is due to the fact that according to Maxwell’s hypothesis, electric displacement obeys the same laws as an incompressible fluid. If, then, \({\bf D}\) is the electric displacement, \[ \hbox{div } {\bf D} = \nabla \,{\cdot}\,{\bf D} = \hbox{0}. \]
Gibbs’ interpretation of curl was much like the one we gave in Example 9 for the rotation of a rigid body. Wilson remarks that an analysis of the meaning of curl for fluid motion was “rather difficult.” It remains a bit elusive, even today, as can be seen from our discussion following Example 9. We provide another interpretation in Chapter 18.