Review Exercises for Chapter 14
Question 14.249
Let \(f\) be any differentiable function. Show that \(u=f(y-kx)\) is a solution to the partial differential equation \(\displaystyle \frac{\partial u}{\partial x} + k\frac{\partial u}{\partial y}=0\).
Question 14.250
Prove that if \(u\) and \(v\) have continuous mixed second partial derivatives and satisfy the Cauchy–Riemann equations \begin{eqnarray*} \frac{\partial u}{\partial x} &=&\frac{\partial v}{\partial y} \\[6pt] \frac{\partial u}{\partial y} &=&-\frac{\partial v}{\partial x}, \end{eqnarray*} then both \(u\) and \(v\) are harmonic.
Question 14.251
Let \(f(x, y)=x^2-y^2-xy+5\). Find all critical points of \(f\) and determine whether they are local minima, local maxima, or saddle points.
Question 14.252
Find the absolute minimum and maximum values of the function \(f(x, y)=x^2+3xy+y^2+5\) on the unit disc \(D=\{(x, y) \mid x^2+y^2 \leq 1\}\).
Question 14.253
Find the second-order Taylor polynomial for \(f(x, y)=y^2e^{-x^2}\) at (1, 1).
Question 14.254
Let \(f(x, y)=ax^2+bxy+cy^2\).
- (a) Find \(g(x, y)\), the second-order Taylor approximation to \(f\) at (0, 0).
- (b) What is the relationship between \(g\) and \(f\)?
- (c) Prove that \(R_2(\textbf{x}_0, \textbf{h}) = 0\) for all \(\textbf{x}_0, \ \textbf{h} \in \mathbb{R}^2\). (HINT: Show that \(f\) is equal to its second-order Taylor approximation at every point.)
Question 14.255
Analyze the behavior of the following functions at the indicated points. [Your answer in part (b) may depend on the constant \(C\).]
- (a) \(z = x^2 -y^2 + 3xy, \qquad (x,y)= (0,0)\)
- (b) \(z = x^2 -y^2 + Cxy, \qquad (x,y)= (0,0)\)
Question 14.256
Find and classify the extreme values (if any) of the functions on \({\mathbb R}^2\) defined by the following expressions:
- (a) \(y^2 - x^3\)
- (b) \((x -1)^2 + (x-y)^2\)
- (c) \(x^2 +xy^2 + y^4\)
Question 14.257
- (a) Find the minimum distance from the origin in \({\mathbb R}^3\) to the surface \(z = \sqrt{x^2 -1}\).
- (b) Repeat part (a) for the surface \(z= 6xy +7\).
212
Question 14.258
Find the first few terms in the Taylor expansion of \(f(x,y)= e^{xy} \cos x\) about \(x=0\), \(y=0\).
Question 14.259
Prove that \[ z=\frac{3x^4-4x^3-12x^2+18}{12(1+4y^2)} \] has one local maximum, one local minimum, and one saddle point. (The graph is shown in Figure 14.72.)
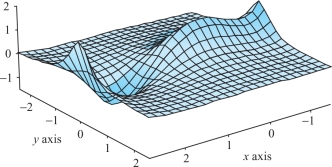
Question 14.260
Find the maxima, minima, and saddles of the function \(z=(2+\cos\pi x)(\sin \pi y)\), which is graphed in Figure 14.73.
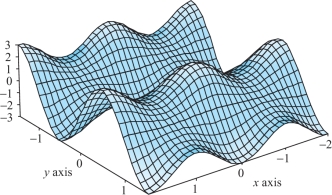
Question 14.261
Find and describe the critical points of \(f(x,y)=y\sin\,(\pi x)\,\). (See Figure 14.74.)
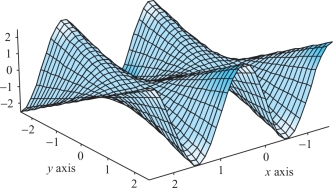
Question 14.262
A graph of the function \(z=\sin(\pi x)/(1+y^2)\) is shown in Figure 14.75. Verify that this function has alternating maxima and minima on the \(x\) axis, with no other critical points.
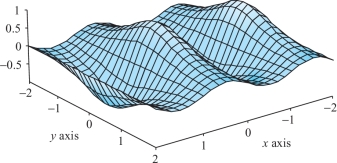
In Exercises 15 to 20, find the extrema of the given functions subject to the given constraints.
Question 14.263
\(f(x,y)=x^2-2xy+2y^2\), subject to \(x^2+y^2=1\)
Question 14.264
\(f(x,y)=xy-y^2\), subject to \(x^2+y^2=1\)
Question 14.265
\(f(x,y)=\cos(x^2-y^2)\), subject to \(x^2+y^2=1\)
Question 14.266
\(f(x,y)=\displaystyle \frac{x^2-y^2}{x^2+y^2}\), subject to \(x+y=1\)
Question 14.267
\(z=xy\), subject to the condition \(x+y = 1\)
Question 14.268
\(z = \cos^2 x + \cos^2 y\), subject to the condition \(x+y = \pi/4\)
Question 14.269
Find the points on the surface \(z^2- xy = 1\) nearest to the origin.
Question 14.270
Use the implicit function theorem to compute \(dy/dx\) for
- (a) \(x/y =10\)
- (b) \(x^3 - \sin y + y^4 = 4\)
- (c) \(e^{x + y^2} + y^3 =0\)
213
Question 14.271
Find the shortest distance from the point \((0, b)\) to the parabola \(x^2-4y = 0\). Solve this problem using the Lagrange multiplier method and also without using Lagrange’s method.
Question 14.272
Determine all values of \(k\) for which the function \(g(x, y, z)=x^2+kxy+kxz+ky^2+kz^2\) has a local minimum at \((0, 0, 0)\).
Question 14.273
Find and classify all critical points of the function \(g(x, y)=\frac{1}{4}x^4-\frac{5}{3}x^3+y^3+3x^2-\frac{3}{2}y^2+20\).
Question 14.274
Solve the following geometric problems by Lagrange’s method.
- (a) Find the shortest distance from the point \((a_1,a_2,a_3)\) in \({\mathbb R}^3\) to the plane whose equation is given by \(b_1 x_1 +b_2 x_2 + b_3 x_3 +b_0 = 0\), where \((b_1,b_2,b_3)\neq (0,0,0).\)
- (b) Find the point on the line of intersection of the two planes \(a_1 x_1 +a_2 x_2 + a_3 x_3 = 0\) and \(b_1 x_1 +b_2 x_2 + b_3 x_3 +b_0 = 0\) that is nearest to the origin.
- (c) Show that the volume of the largest rectangular parallelepiped that can be inscribed in the ellipsoid \[ \frac{x^2}{a^2} +\frac{y^2}{b^2} +\frac{z^2}{c^2} =1 \] is \(8abc/3\sqrt{3}\).
Question 14.275
A particle moves in a potential \(V(x,y)= x^3 - y^2 + x^2 + 3xy\). Determine whether (0, 0) is a stable equilibrium point; that is, whether or not \((0,0)\) is a strict local minimum of \(V\).
Question 14.276
Study the nature of the function \(f(x,y)=x^3 - 3xy^2\) near (0, 0). Show that the point (0, 0) is a degenerate critical point; that is, \(D=0\). This surface is called a monkey saddle.
Question 14.277
Find the maximum of \(f(x,y) = xy\) on the curve \((x+1)^2 + y^2 = 1\).
Question 14.278
Find the maximum and minimum of \(f(x,y) = xy - y +x -1\) on the set \(x^2 + y^2 \leq 2\).
Question 14.279
The Baraboo, Wisconsin, plant of International Widget Co., Inc., uses aluminium, iron, and magnesium to produce high-quality widgets. The quantity of widgets that may be produced using \(x\) tons of aluminum, \(y\) tons of iron, and \(z\) tons of magnesium is \(Q(x,y,z) = xyz\). The cost of raw materials is aluminum, $6 per ton; iron, $4 per ton; and magnesium, $8 per ton. How many tons each of aluminum, iron, and magnesium should be used to manufacture 1000 widgets at the lowest possible cost? (HINT: Find an extreme value for what function subject to what constraint.)
Question 14.280
Let \(f{:}\, \,{\mathbb R}\rightarrow {\mathbb R}\) be of class \(C^1\) and let \begin{eqnarray*} u &=& f(x)\\ v &=& -y + xf(x). \end{eqnarray*} If \(f'(x_0) \neq 0\), show that this transformation of \({\mathbb R}^2\) to \({\mathbb R}^2\) is invertible near \((x_0,y_0)\) and its inverse is given by \begin{eqnarray*} x &=& f^{-1}(u)\\ y &=& -v + uf^{-1}(u). \end{eqnarray*}
Question 14.281
Show that the pair of equations \begin{eqnarray*} x^2 -y^2 - u^3 + v^2 + 4 &=& 0\\ 2xy + y^2 - 2u^2 + 3v^4 + 8 &=& 0 \end{eqnarray*} determine functions \(u(x,y)\) and \(v(x,y)\) defined for \((x, y)\) near \(x=2\) and \(y=-1\) such that \(u(2,-1)=2\) and \(v(2,-1)=1\). Compute \(\partial u/ \partial x\) at \((2, -1)\).
Question 14.282
Show that there are positive numbers \(p\) and \(q\) and unique functions \(u\) and \(v\) from the interval \((-1-p,-1 +p)\) into the interval \((1-q, 1+q)\) satisfying \[ xe^{u(x)} + u(x)e^{v(x)} = 0 = xe^{v(x)} + v(x)e^{u(x)} \] for all \(x\) in the interval \((-1 -p, -1 +p)\) with \(u(-1)= 1 = v(-1)\).
Question 14.283
To work this exercise, you should be familiar with the technique of diagonalizing a \(2 \times 2\) matrix. Let \(a(x), b(x)\), and \(c(x)\) be three continuous functions defined on \(U \cup \partial U\), where \(U\) is an open set and \(\partial U\) denotes its set of boundary points (see Section 2.2). Use the notation of Lemma 2 in Section 14.3, and assume that for each \(x \in U \cup \partial U\) the quadratic form defined by the matrix \[ \left[\begin{array}{c@{\quad}c} a &b\\ b& c \end{array}\right] \] is positive-definite. For a \(C^2\) function \(v\) on \(U\cup \partial U\), we define a differential operator \({\bf L}\) by \[ {\bf L} v = a(\partial^2 v/ \partial x^2) + 2b(\partial^2 v /\partial x \partial y) + c(\partial^2 v/\partial y^2). \] With this positive-definite condition, such an operator is said to be elliptic. A function \(v\) is said to be strictly subharmonic relative to L if \({\bf L} v >0\). Show that a strictly subharmonic function cannot have a maximum point in \(U\).
214
Question 14.284
A function \(v\) is said to be in the kernel of the operator \({\bf L}\) described in Exercise 35 if \({\bf L} v =0\) on \(U \cup \partial U\). Arguing as in Exercise 47 of Section 14.3, show that if \(v\) achieves its maximum on \(U\), it also achieves it on \(\partial U\). This is called the weak maximum principle for elliptic operators.
Question 14.285
Let \({\bf L}\) be an elliptic differential operator as in Exercises 35 and 36.
- (a) Define the notion of a strict superharmonic function.
- (b) Show that such functions cannot achieve a minimum on \(U\).
- (c) If \(v\) is as in Exercise 36, show that if \(v\) achieves its minimum on \(U\), it also achieves it on \(\partial U\).
Question 14.286
Consider the surface \(S\) given by \(x^2z+x\sin y+ye^{z-1}=1\).
- (a) Find the equation of the tangent plane to \(S\) at the point (1, 0, 1).
- (b) Is it possible to solve the equation defining \(S\) for the variable \(y\) as a function of the variables \(x\) and \(z\) near (1, 0, 1)? Why?
- (c) Find \(\frac{\partial y}{\partial x}\) at (1, 0, 1).
Question 14.287
Consider the system of equations \begin{eqnarray*} 2xu^3v-yv=1\\ y^3v+x^5u^2=2 \end{eqnarray*} Show that near the point \((x, y, u, v)= (1, 1, 1, 1)\), this system defines \(u\) and \(v\) implicitly as functions of \(x\) and \(y\). For such local functions \(u\) and \(v\), define the local function \(f\) by \(f(x, y)=(u(x, y), v(x, y))\). Find \(Df(1, 1)\).
The following method of least squares should be applied to Exercises 40 to 45.
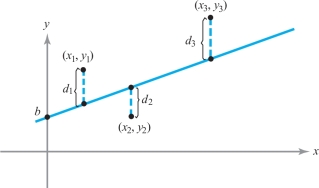
It sometimes happens that the theory behind an experiment indicates that the experimental data should lie approximately along a straight line of the form \(y = mx +b\). The actual results, of course, never match the theory exactly. We are then faced with the problem of finding the straight line that best fits some set of experimental data \((x_1,y_1),\ldots,\) \((x_n,y_n)\) as in Figure 14.76. If we guess at a straight line \(y = mx +b\) to fit the data, each point will deviate vertically from the line by an amount \(d_i = y_i - (mx_i + b)\).
We would like to choose \(m\) and \(b\) in such a way as to make the total effect of these deviations as small as possible. However, because some are negative and some positive, we could get a lot of cancellations and still have a pretty bad fit. This leads us to suspect that a better measure of the total error might be the sum of the squares of these deviations. Thus, we are led to the problem of finding the \(m\) and \(b\) that minimize the function \[ s = f(m,b)= d_1^2 + d^2_2 + \cdots + d_n^2 = \sum_{i=1}^n\,(y_i - mx_i - b)^2, \] where \(x_1,\ldots,x_n\) and \(y_1,\ldots,y_n\) are the given data.
Question 14.288
For each set of three data points, plot the points, write down the function \(f(m,b)\) from the preceding equation, find \(m\) and \(b\) to give the best straight-line fit according to the method of least squares, and plot the straight line.
- (a) \(\begin{array}[t]{c} (x_1,y_1) = (1,1)\\ (x_2,y_2) = (2,3) \\ (x_3,y_3) = (4,3) \end{array}\)
- (b) \(\begin{array}[t]{c} (x_1,y_1) = (0,0)\\ (x_2,y_2) = (1,2)\\ (x_3,y_3) = (2,3) \end{array}\)
Question 14.289
Show that if only two data points \((x_1,y_1)\) and \((x_2,y_2)\) are given, this method produces the line through \((x_1,y_1)\) and \((x_2,y_2)\).
Question 14.290
Show that the equations for a critical point, \(\partial s/\partial b =0\) and \(\partial s /\partial m =0\), are equivalent to \[ m\bigg(\sum x_i\bigg)+ nb = \bigg(\sum y_i\bigg) \] and \[ m\bigg(\sum x_i^2\bigg)+ b\bigg(\sum x_i\bigg) = \bigg(\sum x_iy_i\bigg), \] where all the sums run from \(i=1\) to \(i=n\).
Question 14.291
If \(y=mx +b\) is the best-fitting straight line to the data points \((x_1,y_1),\ldots,(x_n,y_n)\) according to the least-square method, show that \[ \sum_{i=1}^n\, (y_i - mx_i - b) =0; \] that is, the positive and negative deviations cancel (see Exercise 42).
215
Question 14.292
Use the second-derivative test to show that the critical point of \(f\) is a minimum.
Question 14.293
Use the method of least squares to find the straight line that best fits the points \((0,1), (1,3),\) \((2,2), (3,4)\), and \((4,5)\). Plot the points and line.footnote #
Question 14.294
The partial differential equation \[ \frac{\partial^4 u}{\partial x^4} =-\frac{1}{c^2}\frac{\partial^2 u}{\partial t^2}, \] where \(c\) is a constant, comes up in the study of deflections of a thin beam. Show that \[ u(x, t)=\sin(\lambda \pi x) \cos(\lambda^2 \pi^2 ct) \] is a solution for any choice of the parameter \(\lambda\).
Question 14.295
The Kortweg–DeVries equation \[ \frac{\partial u}{\partial t} +u\frac{\partial u}{\partial x} +\frac{\partial^3 u}{\partial x^3} =0 \] arises in modeling shallow water waves (called \(\textbf{solitons}\)). Show that \[ u(x, t)=12a^2 \hbox{sech}^2(ax-4a^3t) \] is a solution to the Kortweg–DeVries equation (see the Internet supplement).
Question 14.296
The heat-conduction equation in two space dimensions is \[ k(u_{xx}+u_{yy})=u_t. \] Assuming that \(u(x, y, t)=X(x)Y(y)T(t)\), find ordinary differential equations satisfied by \(X(x), Y(y)\), and \(T(t)\).
Question 14.297
The heat conduction equation in two space dimensions may be expressed in terms of polar coordinates as \[ k\Big(u_{rr}+ \frac{1}{r}u_r+ \frac{1}{r^2}u_{\theta \theta}\Big) =u_t. \] Assuming that \(u(r, \theta, t)=R(r)\Theta(\theta)T(t)\), find ordinary differential equations satisfied by \(R(r), \Theta(\theta)\), and \(T(t)\).
Question 14.298
Let \(\textbf{F}(x, y, z)=(\sin(xz), e^{xy}, x^2y^3z^5)\).
- (a) Find the divergence of \(\textbf{F}\).
- (b) Find the curl of \(\textbf{F}\).
Question 14.299
Verify that the gravitational force field \(\textbf{F}(x, y, z)=-A\displaystyle\frac{(x, y, z)}{(x^2+y^2+z^2)^{3/2}}\), where \(A\) is some constant, is curl free away from the origin.
261
Question 14.300
Show that the vector field \(\textbf{V}(x, y, z)=2x\textbf{i} -3y\textbf{j}+4z\textbf{k}\) is not the curl of any vector field.
Question 14.301
A particle of mass \(m\) moves under the influence of a force \({\bf F}=-k{\bf r}\), where \(k\) is a constant and \({\bf r}(t)\) is the position of the particle at time \(t\).
- (a) Write down differential equations for the components of \({\bf r}(t)\).
- (b) Solve the equations in part (a) subject to the initial conditions \({\bf r}(0)={\bf 0}, {\bf r}'(0)=2{\bf j}+{\bf k}\).
Question 14.302
Show that \({\bf c}(t)=(1/(1-t),0,e^t/(1-t))\) is a flow line of the vector field defined by \({\bf F}(x,y,z)=(x^2,0,\) \(z(1+x))\).
Question 14.303
Let \({\bf F}(x,y)=f(x^2+y^2)[-y{\bf i}+x{\bf j}]\) for a function \(f\) of one variable. What equation must \(g(t)\) satisfy for \[ {\bf c}(t)=[\cos g(t)]{\bf i}+[\sin g(t)]{\bf j} \] to be a flow line for \({\bf F}\)?
Compute \(\nabla \,{\cdot}\, {\bf F}\) and \(\nabla \times {\bf F}\,\) for the vector fields in the next three Exercises.
Question 14.304
\({\bf F}=2x{\bf i}+3y{\bf j}+4z{\bf k}\)
Question 14.305
\({\bf F}=x^2{\bf i}+y^2{\bf j}+z^2{\bf k}\)
Question 14.306
\({\bf F}=(x+y){\bf i}+(y+z){\bf j}+(z+x){\bf k}\)
Question 14.307
\({\bf F}=x{\bf i}+3xy{\bf j}+z{\bf k}\)
Compute the divergence and curl of the vector fields in Exercises 25 and 26 at the points indicated.
Question 14.308
\({\bf F}(x,y,z)=y{\bf i}+z{\bf j}+x{\bf k}\), at the point (1, 1, 1)
Question 14.309
\({\bf F}(x,y,z)=(x+y)^3{\bf i}+(\sin xy){\bf j}+(\cos xyz){\bf k}\), at the point (2, 0, 1)
Calculate the gradients of the functions in Exercises 27 to 30, and verify that \(\nabla \times \nabla f={\bf 0}.\)
Question 14.310
\(f(x,y)=e^{xy}+\cos\, (xy)\)
Question 14.311
\(f(x,y)=\displaystyle\frac{x^2-y^2}{x^2+y^2}\)
Question 14.312
\(f(x,y)=e^{x^2}-\cos\, (xy^2)\)
Question 14.313
\(f(x,y)=\tan^{-1}\,(x^2+y^2)\)
Question 14.314
- (a) Let \(f(x,y,z) = xyz^2;\) compute \(\nabla f\).
- (b) Let \({\bf F}(x,y,z) =xy{\bf i}+yz{\bf j}+zy{\bf k}\); compute \(\nabla \times {\bf F}\).
- (c) Compute \(\nabla \times (f {\bf F})\) using identity 10 of the list of vector identities. Compare with a direct computation.
Question 14.315
- (a) Let \({\bf F}=2xye^z{\bf i}+e^zx^2{\bf j}+(x^2ye^z+z^2){\bf k}\). Compute \(\nabla\,{\cdot}\, {\bf F}\) and \(\nabla \times {\bf F}.\)
- (b) Find a function \(f(x,y,z)\) such that \({\bf F}=\nabla f\).
Question 14.316
Let \({\bf F}(x,y)=f(x^2+y^2)[-y{\bf i}+x{\bf j}]\), as in Exercise 20. Calculate div \({\bf F}\) and curl \({\bf F}\) and discuss your answers in view of the results of Exercise 20.
Question 14.317
Let a particle of mass \(m\) move along the elliptical helix \({\bf c}(t)\,{=}\,(4 \cos t, \sin t, t)\).
- (a) Find the equation of the tangent line to the helix at \(t=\pi /4\).
- (b) Find the force acting on the particle at time \(t=\pi /4\).
- (c) Write an expression (in terms of an integral) for the arc length of the curve \({\bf c}({t})\) between \(t= 0\) and \(t=\pi /4\).
262
Question 14.318
- (a) Let \(g(x, y, z)=x^{3} + 5{\it yz} + z^{2}\) and let \(h(u)\) be a function of one variable such that \(h' (1) = 1/2\). Let \(f=h \circ g\). Starting at (1, 0, 0), in what directions is \(f\) changing at 50&percent; of its maximum rate?
- (b) For \(g(x, y, z)=x^{3} + 5{\it yz} + z^{2}\), calculate \({\bf F}\,{=}\,\nabla g\), the gradient of \(g\), and verify directly that \(\nabla \times {\bf F} = 0\) at each point (\(x, y, z)\).
Question 14.319
- (a) Write in parametric form the curve that is the intersection of the surfaces \(x^2+y^2+z^2=3\) and \(y=1\).
- (b) Find the equation of the line tangent to this curve at (1, 1, 1).
- (c) Write an integral expression for the arc length of this curve. What is the value of this integral?
Question 14.320
In meteorology, the negative pressure gradient \({\bf G}\) is a vector quantity that points from regions of high pressure to regions of low pressure, normal to the lines of constant pressure (isobars).
- (a) In an \(xy\) coordinate system, \[ {\bf G}=-\frac{\partial P}{\partial x}{\bf i}-\frac{\partial P}{\partial y}{\bf j}. \] Write a formula for the magnitude of the negative pressure gradient.
- (b) If the horizontal pressure gradient provided the only horizontal force acting on the air, the wind would blow directly across the isobars in the direction of \({\bf G}\), and for a given air mass, with acceleration proportional to the magnitude of \({\bf G}\). Explain, using Newton’s second law.
- (c) Because of the rotation of the earth, the wind does not blow in the direction that part (b) would suggest. Instead, it obeys Buys–Ballot’s law, which states: “If in the Northern Hemisphere, you stand with your back to the wind, the high pressure is on your right and the low pressure is on your left.” Draw a figure and introduce \(xy\) coordinates so that \({\bf G}\) points in the proper direction.
- (d) State and graphically illustrate Buys–Ballot’s law for the Southern Hemisphere, in which the orientation of high and low pressure is reversed.
Question 14.321
A sphere of mass \(m\), radius \(a\), and uniform density has potential \(u\) and gravitational force \({\bf F}\), at a distance \(r\) from the center (0, 0, 0), given by \begin{eqnarray*} u=\frac{3m}{2a}-\frac{mr^2}{2a^3},{\bf F}&=&-\frac{m}{a^3}{\bf r}\qquad(r\leq a);\\[6pt] u=\frac{m}{r},{\bf F}&=&-\frac{m}{r^3}{\bf r}\qquad(r >a).\\[-11pt] \end{eqnarray*} Here, \(r=\|{\bf r}\|,{\bf r}=x{\bf i}+y{\bf j}+ z{\bf k}\).
- (a) Verify that \({\bf F}=\nabla u\) on the inside and outside of the sphere.
- (b) Check that \(u\) satisfies Poisson’s equation: \(\partial^2 u/\partial x^2+ \partial^2 u/\partial y^2+\partial^2 u/\partial z^2=\) constant inside the sphere.
- (c) Show that \(u\) satisfies Laplace’s equation: \(\partial^2 u/\partial x^2+\partial^2 u/\partial y^2+\partial^2 u/\partial z^2=0\) outside the sphere.
Question 14.322
A circular helix that lies on the cylinder \(x^2+y^2=R^2\) with pitch \(\rho\) may be described parametrically by \[ x=R\cos \theta,\qquad y=R\sin \theta,\qquad z=\rho \theta,\qquad \theta \geq 0. \] A particle slides under the action of gravity (which acts parallel to the \(z\) axis) without friction along the helix. If the particle starts out at the height \(z_0 >0\), then when it reaches the height \(z\) along the helix, its speed is given by \[ \frac{{\it ds}}{{\it dt}}=\sqrt{(z_0-z)2g}, \] where \(s\) is arc length along the helix, \(g\) is the constant of gravity, \(t\) is time, and \(0 \leq z\leq z_0\).
- (a) Find the length of the part of the helix between the planes \(z=z_0\) and \(z=z_1,0\leq z_1 <z_0\).
- (b) Compute the time \(T_0\) it takes the particle to reach the plane \(z=0\).
Question 14.323
A sphere of radius 10 centimeters (cm) with center at \((0,\,0,\,0)\) rotates about the \(z\) axis with angular velocity 4 in such a direction that the rotation looks counterclockwise from the positive \(z\) axis.
- (a) Find the rotation vector \({\omega}\) (see Example 9, in Section #).
- (b) Find the velocity \({\bf v}={\omega} \times {\bf r}\) when \({\bf r}=5\sqrt{2}({\bf i}-{\bf j})\) is on the “equator.”
- (c) Find the velocity of the point (0, \(5\sqrt{3}\), 5) on the sphere.
Question 14.324
Find the speed of the students in a classroom located at a latitude 49\(^{\circ}\)N due to the rotation of the earth. (Ignore the motion of the earth about the sun, the sun in the galaxy, etc.; the radius of the earth is 3960 miles.)
216
1Recall that integration by parts (the product rule for the derivative read backward) reads as: \[ \int_a^b u\,dv=uv|_a^b -\int_a^b v\,du. \] Here we choose \(u=f'(\tau )\) and \(v=x_{0}+h- \tau\).
2For the statement of the theorem as given here, \(f\) actually needs only to be of class \(C^2\), but for a convenient form of the remainder we assume \(f\) is of class \(C^3\).
3Proof If \(g=0\), the result is clear, so we can suppose \(g\neq 0\); thus, we can assume \(\int_a^b g(t) \,{\it dt} > 0\). Let \(M\) and \(m\) be the maximum and minimum values of \(h\), achieved at \(t_M\) and \(t_m\), respectively. Because \(g(t) \ge 0\), \[ m \int_a^b g(t) \,{\it dt} \le \int_a^b h(t) g(t) \,{\it dt} \le M \int_a^b g(t) \,{\it dt}. \] Thus, \(\big(\int_a^bh(t)g(t) \,{\it dt}\big)\big/\big(\int_a^bg(t) \,{\it dt}\big)\) lies between \(m =h(t_m)\) and \(M=h(t_M)\) and therefore, by the intermediate-value theorem, equals \(h(c)\) for some intermediate \(c\).
4The term “saddle point” is sometimes not used this generally; we shall discuss saddle points further in the subsequent development.
5Recall the proof from one-variable calculus: Because \(g(0)\) is a local maximum, \(g(t) \le g(0)\) for small \(t > 0\), so \(g(t) - g(0) \le 0\), and hence \(g'(0) = {{\rm limit}_{t\to 0^+}}\,(g(t) - g(0))/t\le 0\), where \({{\rm limit}_{t\to 0^+}}\) means the limit as \(t \to 0\), \(t > 0\). For small \(t < 0\), we similarly have \(g'(0) = {{\rm limit}_{t\to 0^-}}\,(g(t) - g(0))/t \ge 0\). Therefore, \(g'(0) =0\).
6Here we are using, without proof, a theorem analogous to a theorem in calculus that states that every continuous function on an interval \([a,b]\) achieves a maximum and a minimum; see Theorem 7.
7This is proved in, for example, K. Hoffman and R. Kunze, Linear Algebra, Prentice Hall, Englewood Cliffs, N.J., 1961, pp. 249–251. For students with sufficient background in linear algebra, it should be noted that \(B\) is positive-definite when all of its eigenvalues (which are necessarily real, because \(B\) is symmetric) are positive.
8This interesting phenomenon was first pointed out by the famous mathematician Giuseppe Peano (1858–1932). Another curious “pathology” is given in Exercise 41.
9In these examples, \({\nabla} g({\bf x}_0)\neq {\bf 0}\) on the surface \(S\), as required by the Lagrange multiplier theorem. If \({\nabla} g({\bf x}_0)\) were zero for some \({\bf x}_0\) on \(S\), then it would have to be included among the possible extrema.
10Dorothy L. Sayers, Have His Carcase, Chapter 31: The Evidence of the Haberdasher’s Assistant, New York, Avon Books, 1968, p. 312.
11As with the hypothesis \({\nabla} g({\bf x}_0) \ne {\bf 0}\) in the Lagrange multiplier theorem, here we must assume that the vectors \({\nabla} g_1({\bf x}_0),\ldots, {\nabla} g_k({\bf x}_0)\) are linearly independent; that is, each \(\nabla {g_i} ({\bf x}_0)\) is not a linear combination of the other \(\nabla {g_j} ({\bf x}_0), j \,{\neq}\, i\).
12The matrix of coefficients of the equations cannot have an inverse, because this would imply that the solution is zero. Recall that a matrix that does not have an inverse has determinant zero.
13For a detailed discussion, see C. Caratheodory, Calculus of Variations and Partial Differential Equations, Holden-Day, San Francisco, 1965; Y. Murata, Mathematics for Stability and Optimization of Economic Systems, Academic Press, New York, 1977, pp. 263–271; or D. Spring, Am. Math. Mon. 92 (1985): 631–643.
14For three different proofs of the general case, consult: (a) E. Goursat, A Course in Mathematical Analysis, I, Dover, New York, 1959, p. 45. (This proof derives the general theorem by successive application of Theorem 11.) (b) T. M. Apostol, Mathematical Analysis, 2d ed., Addison-Wesley, Reading, Mass., 1974. (c) J. E. Marsden and M. Hoffman, Elementary Classical Analysis, 2d ed., Freeman, New York, 1993. Of these sources, the last two use more sophisticated ideas that are usually not covered until a junior-level course in analysis. The first, however, is easily understood by the reader who has some knowledge of linear algebra.
15For students who have had linear algebra: The condition \(\Delta\neq 0\) has a simple interpretation in the case that \(F\) is linear; namely, \(\Delta\neq 0\) is equivalent to the rank of \(F\) being equal to \(m\), which in turn is equivalent to the fact that the solution space of \(F=0\) is m-dimensional.
16The method of least squares may be varied and generalized in a number of ways. The basic idea can be applied to equations of more complicated curves than the straight line. For example, this might be done to find the parabola that best fits a given set of data points. These ideas also formed part of the basis for the development of the science of cybernetics by Norbert Wiener. Another version of the data is the following problem of least-square approximation: Given a function \(f\) defined and integrable on an interval \([a,b]\), find a polynomial \(P\) of degree \({\leq} n\) such that the mean square error \[ \int^b_a {\mid} f(x) - P(x) |^2 \,dx \] is as small as possible.