Exercises for Section 15.5
Question 15.84
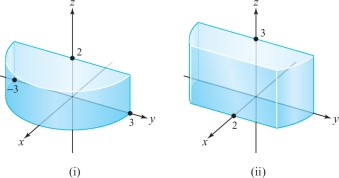
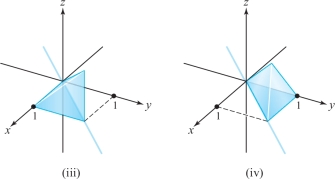
In parts (a) through (d) below, each iterated integral is an integral over a region \(D\). Match the integral with the correct region of integration.
- (a) \(\displaystyle\int_{0}^{2} \int_{0}^{3} \int_{-\sqrt{9-x}}^{\sqrt{9-x}} \, {\it dy}\, {\it dz}\, {\it dx}\)
- (b) \(\displaystyle\int_{0}^{2} \int_{0}^{3} \int_{-\sqrt{9-x^{2}}}^{\sqrt{9-x^{2}}} \, {\it dy}\, {\it dx}\, {\it dz}\)
- (c) \(\displaystyle\int_{0}^{1} \int_{0}^{x} \int_{0}^{y} \, {\it dz}\, {\it dy}\, {\it dx}\)
- (d) \(\displaystyle\int_{0}^{1} \int_{0}^{y} \int_{0}^{x} \, {\it dz}\, {\it dx}\, {\it dy}\)
Question 15.85
Evaluate the following triple integral: \[ \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} \sin x \, {\it dx}\, {\it dy}\, {\it dz}, \] where \(W\) is the solid given by \(0 \leq x \leq \pi\), \(0 \leq y \leq 1\), and \(0 \leq z \leq x\).
In the next four exercises, perform the indicated integration over the given box.
303
Question 15.86
\(\displaystyle\int\!\!\!\int\!\!\!\int_B x^2{\it dx}\,{\it dy}\,{\it dz},B=[0,1]\times [0,1]\times [0,1]\)
Question 15.87
\(\displaystyle\int\!\!\!\int\!\!\!\int_B e^{-xy}\,y\,{\it dx}\,{\it dy}\,{\it dz},B=[0,1]\times [0,1]\times [0,1]\)
Question 15.88
\(\displaystyle\int\!\!\!\int\!\!\!\int_B (2x+3y+z)\,{\it dx}\,{\it dy}\,{\it dz},B=[0,2]\times [-1,1]\times [0,1]\)
Question 15.89
\(\displaystyle\int\!\!\!\int\!\!\!\int_B ze^{x+y}{\it dx}\,{\it dy}\,{\it dz},B=[0,1]\times [0,1]\times [0,1]\)
In the next four exercises, describe the given region as an elementary region.
Question 15.90
The region between the cone \(z=\sqrt{x^2+y^2}\) and the paraboloid \(z=x^2+y^2\)
Question 15.91
The region cut out of the ball \(x^2+y^2+z^2\leq 4\) by the elliptic cylinder \(2x^2+z^2=1\); that is, the region inside the cylinder and the ball
Question 15.92
The region inside the sphere \(x^2+y^2 +z^2=1\) and above the plane \(z=0\)
Question 15.93
The region bounded by the planes \(x=0,y=0, z=0, x+y=4,\) and \(x=z-y-1\)
Find the volume of the region in the next four exercises.
Question 15.94
The region bounded by \(z=x^2+y^2\) and \(z=10-x^2-2y^2\)
Question 15.95
The solid bounded by \(x^2+2y^2=2,z=0\), and \(x+y+2z=2\)
Question 15.96
The solid bounded by \(x=y,z=0,y=0,x=1,\) and \(x+y+z=0\)
Question 15.97
The region common to the intersecting cylinders \(x^2+y^2\leq a^2\) and \(x^2+z^2\leq a^2\)
Evaluate the integrals in the next ten exercises.
Question 15.98
\(\displaystyle\int^1_0\int^2_1\int^3_2 \cos\, [\pi(x+y+z)]\,{\it dx}\,{\it dy}\,{\it dz}\)
Question 15.99
\(\displaystyle\int^1_0\int^x_0\int^y_0 (y+xz)\,{\it dz}\,{\it dy}\,{\it dx}\)
Question 15.100
\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W (x^2+y^2+z^2)\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the region bounded by \(x+y+z=a\) (where \(a > 0\)), \(x=0,y=0\), and \(z=0\).
Question 15.101
\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W z\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the region bounded by the planes \(x=0,y=0,z=0,z=1,\) and the cylinder \(x^2+y^2=1\), with \(x\geq 0,y\geq 0\).
Question 15.102
\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W x^2\cos z{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the region bounded by \(z=0,z=\pi,y=0, y=1,x=0,\) and \(x+y=1\).
Question 15.103
\(\displaystyle\int^2_0\int^x_0\int^{x+y}_0{\it dz}\,{\it dy}\,{\it dx}\)
Question 15.104
\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W(1-z^2)\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the pyramid with top vertex at \((0,0,1)\) and base vertices at \((0,0,0)\), \((1,0,0)\), \((0,1,0),\) and \((1,1,0)\).
Question 15.105
\(\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_W(x^2+y^2)\,{\it dx}\,{\it dy}\,{\it dz}\); \(W\) is the same pyramid as in Exercise 21.
Question 15.106
\(\displaystyle\int^1_0\int^{2x}_0\int^{x+y}_{x^2+y^2}{\it dz}\,{\it dy}\,{\it dx}.\)
Question 15.107
- (a) Sketch the region for the integral \(\displaystyle\int^1_0\int^x_0\int^y_0 f(x,y,z)\,{\it dz}\,{\it dy}\,{\it dx}.\)
- (b) Write the integral with the integration order \({\it dx}\,{\it dy}\,{\it dz}\).
For the regions in the next four exercises, find the appropriate limits \(\phi_1(x),\phi_2(x),\gamma_1(x,y),\) and \(\gamma_2(x,y),\) and write the triple integral over the region W as an iterated integral in the form \[ \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} f {\,d} V=\int^b_a \bigg\{ \int^{\phi_2(x)}_{\phi_1(x)}\bigg[\int^{\gamma_2(x,y)}_{\gamma_1(x,y)} f(x,y,z)\,{\it dz}\bigg]\,{\it dy}\bigg\}\,{\it dx}. \]
304
Question 15.108
\(W=\{(x,y,z)\mid \sqrt{x^2+y^2}\leq z\leq 1\}\)
Question 15.109
\(W=\{(x,y,z)\mid \frac{1}{2}\leq z\leq 1\) and \(x^2+y^2+z^2\leq 1\}\)
Question 15.110
\(W=\{(x,y,z)\mid x^2+y^2\leq 1, z\geq 0\) and \(x^2+y^2+z^2\leq 4\}\)
Question 15.111
\(W=\{(x,y,z)\mid |x|\leq 1, |y|\leq 1, z\geq 0\) and \(x^2+y^2+z^2\leq 1\}\)
Question 15.112
Show that the formula using triple integrals for the volume under the graph of a positive function \(f(x,y),\) on an elementary region \(D\) in the plane, reduces to the double integral of \(f\) over \(D\).
Question 15.113
Let \(W\) be the region bounded by the planes \(x=0,y=0,z=0,x+y=1,\) and \(z=x+y\).
- (a) Find the volume of \(W\).
- (b) Evalute \({\intop\!\!\!\intop\!\!\!\intop}_W x{\it dx}\,{\it dy}\,{\it dz}\).
- (c) Evalute \({\intop\!\!\!\intop\!\!\!\intop}_W y{\it dx}\,{\it dy}\,{\it dz}\).
Question 15.114
Let \(f\) be continuous and let \(B_\varepsilon\) be the ball of radius \(\varepsilon\) centered at the point \((x_0,y_0,z_0)\). Let vol (\(B_{\varepsilon}\)) be the volume of \(B_\varepsilon\). Prove that \[ \lim_{\varepsilon \rightarrow 0} \frac{1}{{\rm vol}\, (B_{\varepsilon})}\intop\!\!\!\intop\!\!\!\intop\nolimits_{B_{\varepsilon}} f(x,y,z){\,d} V=f(x_0,y_0,z_0). \]