Question 15.115

\(\displaystyle\int^3_0\!\int^{x^2 +1}_{-x^2 +1} {\it xy}\, {\it dy}\, {\it dx} \)

Question 15.116

\(\displaystyle\int^1_0\!\int^{1}_{\sqrt{x}}\, (x + y)^2 {\it dy}\, {\it dx} \)

Question 15.117

\(\displaystyle\int^1_0\!\int^{e^{2x}}_{e^x} x \ln y\, {\it dy}\, {\it dx} \)

Question 15.118

\(\displaystyle\int^1_0\!\int^2_1\!\int^3_2\cos\, [\pi(x+y+z)]\,{\it dx}\,{\it dy}\,{\it dz}.\)

Question 15.119

The integral in the first exercise.

Question 15.120

The integral in the second exercise.

Question 15.121

The integral in the third exercise.

Question 15.122

The integral in the fourth exercise.

Question 15.123

Evaluate the integral \(\int^1_0\int^x_0\int^y_0(y+xz)\,dz\,{\it dy}\,{\it dx}.\)

Question 15.124

Evaluate \(\int^1_0\int^{y^2}_ye^{x/y}\,{\it dx}\,{\it dy}.\)

Question 15.125

Evaluate \(\int^1_0\int^{\rm (arcsin\, {\it y})/{\it y}}_0 y\cos xy\,{\it dx}\,{\it dy}.\)

Question 15.126

Change the order of integration and evaluate \[ \int^2_0 \int^1_{y/2} (x + y)^2 {\it dx}\, {\it dy} . \]

Question 15.127

Show that evaluating \({\intop\!\!\!\intop}_D {\it dx}\, {\it dy} \), where \(D\) is a \(y\)-simple region, reproduces the formula from one-variable calculus for the area between two curves.

Question 15.128

Change the order of integration and evaluate \[ \int^1_0 \int^1_{y^{1/2}} (x^2 + y^3 x)\, {\it dx}\, {\it dy} . \]

Question 15.129

Let \(D\) be the region in the \(xy\) plane inside the unit circle \(x^2 + y^2 = 1\). Evaluate \({\intop\!\!\!\intop}_D f(x,y)\, {\it dx}\, {\it dy}\) in each of the following cases:

• (a) \(f(x,y) = xy\)
• (b) \(f(x,y) = x^2 y^2\)
• (c) \(f(x,y) = x^3 y^3\)

Question 15.130

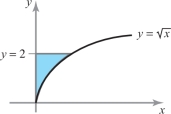
Find \({\intop\!\!\!\intop}_D y[1-\cos\, (\pi x/4)] {\it dx}\, {\it dy} \), where \(D\) is the region in Figure 15.38.

Question 15.131

\(\displaystyle\int^{\pi}_0 \int^{3 \sin x}_{\sin x} x(1 + y)\, {\it dy}\, {\it dx} \)

Question 15.132

\(\displaystyle\int^{1}_0 \int^{x \cos\, (\pi x/2)}_{x-1} (x^2 +xy +1)\, {\it dy}\, {\it dx} \)

Question 15.133

\(\displaystyle\int^{1}_{-1} \int^{(2-y)^2}_{y^{2/3}} \left(\frac{3}{2}\sqrt{x} - 2y\right)\, {\it dx}\, {\it dy}\)

Question 15.134

\(\displaystyle\int^{2}_0 \int^{3 (\sqrt{4 - x^2})/2}_{-3 (\sqrt{4 - x^2})/2} \left({\displaystyle \frac{5}{\sqrt{2+x}}} + y^3\right) \! {\it dy}\, {\it dx} \)

Question 15.135

\(\displaystyle\int^{1}_{0} \int^{x^2}_0 (x^2 + xy -y^2)\, {\it dy}\, {\it dx} \)

Question 15.136

\(\displaystyle\int^{4}_{2} \int^{y^3}_{y^2-1} 3 {\it dx}\, {\it dy} \)

Question 15.137

\(\displaystyle\int^{1}_{0} \int^{x}_{x^2} (x + y)^2 {\it dy}\, {\it dx} \)

Question 15.138

\(\displaystyle\int^{1}_{0} \int^{3y}_{0} e^{x+y} {\it dx}\, {\it dy} \)

Question 15.139

\(f(x,y) = x-y\); \(D\) is the triangle with vertices (0, 0), (1, 0), and (2, 1).

Question 15.140

\(f(x,y) = x^3 y + \cos x\); \(D\) is the triangle defined by \(0 \leq x \leq \pi/2, 0 \leq y \leq x\).

Question 15.141

\(f(x,y) = x^2 + 2xy^2 +2\); \(D\) is the region bounded by the graph of \(y = -x^2 + x\), the \(x\) axis, and the lines \(x = 0\) and \(x = 2\).

Question 15.142

\(\displaystyle\int^{4}_{1} \int^{\sqrt{x}}_1 (x^2 + y^2)\, {\it dy}\, {\it dx} \)

Question 15.143

\(\displaystyle\int^{1}_{0} \int^{1}_{1-y} (x+ y^2)\, {\it dx}\, {\it dy} \)

Question 15.144

Show that \[ 4e^5 \leq \intop\!\!\!\intop\nolimits_{[1,3]\times [2,4]} e^{x^2 + y^2} {\it dA} \leq 4e^{25}. \]

Question 15.145

Show that \[ 4\pi \leq \intop\!\!\!\intop\nolimits_{D} ({x^2 + y^2 +1})\, {\it dx}\, {\it dy} \leq 20 \pi, \] where \(D\) is the disk of radius 2 centered at the origin.

Question 15.146

Suppose \(W\) is a path-connected region; that is, given any two points of \(W\) there is a continuous path joining them. If \(f\) is a continuous function on \(W\), use the intermediate-value theorem to show that there is at least one point in \(W\) at which the value of \(f\) is equal to the average of \(f\) over \(W\); that is, the integral of \(f\) over \(W\) divided by the volume of \(W\). (Compare this with the mean-value theorem for double integrals.) What happens if \(W\) is not connected?

Question 15.147

Prove: \(\int^x_0 [ \int^t_0 F(u)\, {\it {\,d} u}] {\it {\,d} t} = \int^x_0 (x-u) F(u) \,{\it du}\).

Question 15.148

\(\displaystyle\int^1_0\int^z_0\int^y_0 xy^2z^3 {\it dx}\,{\it dy}\,{\it dz}\)

Question 15.149

\(\displaystyle\int^1_0\int^y_0\int_0^{x/\sqrt{3}}\displaystyle \frac{x}{x^2+z^2}{\it dz}\,{\it dx}\,{\it dy}\)

Question 15.150

\(\displaystyle\int^2_1\int^z_1\int^2_{1/y}yz^2 {\it dx}\,{\it dy}\,{\it dz}\)

Question 15.151

Write the iterated integral \(\int^1_0\int^1_{1-x}\int^1_xf(x,y,z)\,{\it dz}\,{\it dy}\,{\it dx}\) as an integral over a region in \({\mathbb R}^3\) and then rewrite it in five other possible orders of integration.