16.2 The Change of Variables Theorem
Given two regions \(D\) and \(D^*\) in \({\mathbb R}^2\), a differentiable map \(T\) on \(D^*\) with image \(D\)—that is, \(T ( D^*) = D\)—and any real-valued integrable function \(f \colon\, D \to {\mathbb R}\), we would like to express \(\intop\!\!\intop\nolimits_D f (x,y) {\,d} A\) as an integral over \(D^*\) of the composite function \(f \circ T\). In this section we shall see how to do this.
Assume that \(D^*\) is a region in the \(uv\) plane and that \(D\) is a region in the \(xy\) plane. The map \(T\) is given by two coordinate functions: \[ T (u,v) = (x (u,v), y (u,v)) \qquad \hbox{for} \qquad (u,v) \in D^*. \]
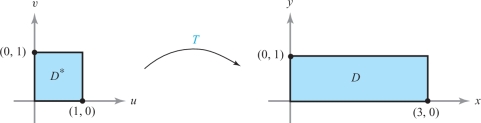
At first, we might conjecture that \begin{equation} \intop\!\!\!\intop\nolimits_{D}\, f (x,y)\, {\it dx}\,{\it dy}\ \ {\displaystyle\mathop =^?} \intop\!\!\!\intop\nolimits_{D^*} f (x (u,v), y(u,v)) {\,d} u{\,d} v, \end{equation} where \(f \circ T (u,v) = f (x (u,v), y (u,v))\) is the composite function defined on \(D^*\). However, if we consider the function \(f \colon\, D \to {\mathbb R}^2\) where \(f (x,y) =1\), then equation (1) would imply \begin{equation} A(D) = \intop\!\!\!\intop\nolimits_{D} {\it dx}\,{\it dy}\ \ {\displaystyle\mathop =^?} \intop\!\!\!\intop\nolimits_{D^*} {\,d} u\ {\,d} v = A ( D^*). \end{equation}
But equation (2) will hold for only a few special cases and not for a general map \(T\). For example, define \(T\) by \(T (u,v) = (- u^2 + 4 u,v)\). Restrict \(T\) to the unit square; that is, to the region \(D^* = [0,1] \times [0,1]\) in the \(uv\) plane (see Figure 16.7). Then, as in Exercise 3, Section 16.1, \(T\) takes \(D^*\) onto \(D = [0,3] \times [0,1]\). Clearly, \(A (D) \ne A (D^*)\), and so formula (2) is not valid.
Jacobian Determinants
315
To rectify the incorrect formula (1), we need a measure of how a transformation \(T{:}\ {\mathbb R}^2 \to {\mathbb R}^2\) distorts the area of a region. This is given by the Jacobian determinant, which is defined as follows.
Definition: Jacobian Determinant
Let \(T{:}\,\, D^* \subset {\mathbb R}^2 \to {\mathbb R}^2\) be a \(C^1\) transformation given by \(x = x (u,v)\) and \(y =y (u,v)\). The Jacobian determinant of \(T\), written \(\partial (x,y) / \partial (u,v)\), is the determinant of the derivative matrix \({\bf D} T (u,v)\) of \(T\): \[ \frac{\partial (x,y)}{\partial (u,v)} = \left | \begin{array}{c@{\quad}c} \\[-8pt] \displaystyle \frac{\partial x}{\partial u} &\displaystyle \frac{\partial x}{\partial v} \\[9pt] \displaystyle \frac{\partial y}{\partial u} &\displaystyle \frac{\partial y}{\partial v}\\[2pt] \\[-8pt] \end{array}\right|. \]
example 1
The function from \({\mathbb R}^2\) to \({\mathbb R}^2\) that transforms polar coordinates into Cartesian coordinates is given by \[ x = r\cos \theta, \qquad y = r \sin \theta \] and its Jacobian determinant is \[ \frac{\partial (x,y)}{\partial (r, \theta)}=\left| \begin{array}{r@{\quad}r} \cos \theta & - r \sin \theta \\ \sin \theta & r \cos \theta \end{array} \right| = r ( \cos^2 \theta + \sin^2 \theta) =r . \]
Question 16.23 Section 16.2 Progress Check Question 1
jpEYYu/EZAeaHrInkcUYa2ITc4UscEcC2MnDOsGqdnMZKO44tFpTmj6t9uzyFWKlYjXn3QMGo+WCGjI39/8mj5xEiD7r2QEMFKnNfXvKRSI5mX6HFcMVDbeyMtsxw8dJ3uef5K8VTS7VmPZITNDbrMU0MB75IGllaQA3tmU5E+FmD0HEOOuU9x02HLvEjVaZRuEzCNHlHaR/oKtIkuV1jZ4J14pOPKkpkkSRZMErupeXr9NTZUhQLTd8DyhU4FyUsA+DVc6Or6OUTcnXe9dlioFtQD6LJjOx88OvgWpXUgigkJYQAvFrpt4cdjFwN/uU0wAe67+Lh8m8xbEXvHT/BZjCkSfAgyRPzh0P22XaSWKewhdHgADjXUUu1pX3PtW0IvW3Uc4fcnrkl3n16zhqGL0LuIQ4X9Ym+c4X+RmsBzHBWfpBX8cF1bOA/vWD5I8I1jgG3/j/nz7NBcl8kM5vLegW3jyL4e2lf+Qs4OWCOJ0Hy6tQwhVtXJfeLgdiLGRLqvQ6P0BOoCBXDuSm7T2RC+II8IkLhFvpKT89mlgiYub0kfQaSg9EehgR2PaaiHEFfpHg2Z3ijQlLQgrvvupdpepQEaiUegMtQspcZbjKaKZTRITT9TC7yfBuX06HohsJZEYnIHi1lUElHLaXT7l7SZrCCExjNLeuQpBxzzMj3Ge5OR9v3qcT0RRU2KuFWd2NkVH971+38D14akNfAT+jUTGTr7kTe7OUwo2YxI3CSw9J+2FA9YvgscJjz6QoIJisWWx7+G4aRhh6PHA1SLWURODXw33xe9eZYBZBpFGfGSdjFFSYG0YnhtYWu/Q=Under suitable restrictions on the function \(T\), we will argue below that the area of \(D = T (D^*)\) is obtained by integrating the absolute value of the Jacobian \(\partial (x,y) / \partial (u,v)\) over \(D^*\); that is, we have the equation \begin{equation} A (D) = \intop\!\!\!\intop\nolimits_{D} {\it dx}\,{\it dy}\ = \intop\!\!\!\intop\nolimits_{D^*} \left| \frac{\partial (x,y)}{\partial (u,v)} \right| {\,d} u{\,d} v. \end{equation}
To illustrate: From Example 1 in Section 16.1, take \(T \colon\, D^* \to D\), where \(D = T ( D^*)\) is the set of \((x,y)\) with \(x^2 + y^2 \le 1\) and \(D^* = [0,1] \times [0, 2 \pi]\), and \(T (r, \theta) = ( r \cos \theta, r \sin \theta)\). By formula (3), \begin{equation} A (D) = \intop\!\!\!\intop\nolimits_{D^*} \left| \frac{ \partial (x,y)}{\partial (r, \theta)} \right| {\,d} r{\,d} \theta = \intop\!\!\!\intop\nolimits_{D^*} r{\,d} r{\,d} \theta \end{equation} (here \(r\) and \(\theta\) play the role of \(u\) and \(v\)). From the preceding computation it follows that \[ \intop\!\!\!\intop\nolimits_{D^*} r{\,d} r {\,d} \theta = \int_0^{2 \pi} \int_0^1 r{\,d} r{\,d} \theta = \int_0^{2 \pi} \left[ \frac{r^2}{2} \right]_0^1 {\,d} \theta = \frac{1}{2} \int_0^{2 \pi} {\,d} \theta = \pi \] is the area of the unit disk \(D\), confirming formula (3) in this case. In fact, we can recall from first-year calculus that equation (4) is the correct formula for the area of a region in polar coordinates.
316
It is not so easy to rigorously prove assertion (3). However, looked at in the proper way, it becomes quite plausible. Recall that \(A (D) = {\intop\!\!\intop}_D {\it dx}\, {\it dy}\) was obtained by dividing up \(D\) into little rectangles, summing their areas, and then taking the limit of this sum as the size of the subrectangles tended to zero. The problem is that \(T\) may map rectangles into regions whose area is not easy to compute. The solution is to approximate these images by simpler regions whose area we can compute. A useful tool for doing this is the derivative of \(T\), which we know (from Chapter 13) gives the best linear approximation to \(T\).
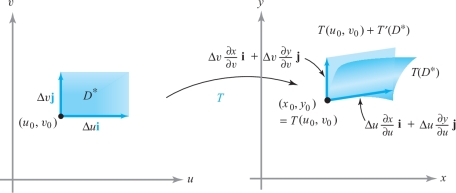
Consider a small rectangle \(D^*\) in the \(uv\) plane as shown in Figure 16.8. Let \(T'\) denote the derivative of \(T\) evaluated at \((u_0,v_0)\), so \(T'\) is a \(2 \times 2\) matrix. From our work in Chapter 13, we know that a good approximation to \(T (u,v)\) is given by \[ T (u_0,v_0) + T' \bigg( \begin{array}{cc} \Delta u\\ \Delta v\end{array} \bigg), \]
where \(\Delta u = u - u_0\) and \(\Delta v = v - v_0\). This mapping \(T'\) takes \(D^*\) into a parallelogram with vertex at \(T (u_0,v_0)\) and with adjacent sides given by the vectors \begin{eqnarray*} T' ( \Delta u\, {\bf i}) = \left[ \begin{array}{c@{\quad}c} \\[-10pt] \displaystyle \frac{\partial x}{\partial u} & \displaystyle \frac{\partial x}{\partial v} \\[9pt] \displaystyle \frac{\partial y}{\partial u} & \displaystyle \frac{\partial y}{\partial v}\\[6pt] \end{array} \right] \left[ \begin{array}{c} \Delta u \\ 0 \end{array} \right] = \Delta u \left[ \begin{array}{c} \\[-10pt] \displaystyle \frac{\partial x}{\partial u}\\[9pt] \displaystyle \frac{\partial y}{\partial u}\\[6pt] \end{array} \right] = \Delta u\, {\bf T}_u \end{eqnarray*} and \begin{eqnarray*} T' ( \Delta v\, {\bf j}) = \left[ \begin{array}{c@{\quad}c} \\[-10pt] \displaystyle \frac{\partial x}{\partial u} & \displaystyle \frac{\partial x}{\partial v} \\[9pt] \displaystyle \frac{\partial y}{\partial u} & \displaystyle \frac{\partial y}{\partial v}\\[6pt] \end{array} \right] \left[ \begin{array}{c} 0 \\ \Delta v \end{array} \right] = \Delta v \left[ \begin{array}{c} \\[-10pt] \displaystyle \frac{\partial x}{\partial v}\\[9pt] \displaystyle \frac{\partial y}{\partial v}\\[6pt] \end{array}\right] = \Delta v\, {\bf T}_v, \end{eqnarray*} where \[ {\bf T}_u = \frac{\partial x}{\partial u} {\bf i} + \frac{\partial y}{\partial u}{ \bf j}\quad \hbox{and}\quad {\bf T}_v = \frac{\partial x}{\partial v} {\bf i} + \frac{\partial y}{\partial v}{ \bf j} \] are evaluated at \((u_0,v_0)\).
317
Recall from Section 11.3 that the area of the parallelogram with sides equal to the vectors \(a {\bf i}+ b {\bf j}\) and \(c {\bf i}+ d {\bf j}\) is equal to the absolute value of the determinant \[ \left| \begin{array}{c@{\quad}c} a & b \\[2pt] c & d \end{array} \right|= \left| \begin{array}{c@{\quad}c} a & c \\[2pt] b & d \end{array} \right|. \]
Thus, the area of \(T ( D^*)\) is approximately equal to the absolute value of \[ \left| \begin{array}{c@{\quad}c} \\[-10pt] \displaystyle \frac{\partial x}{\partial u} \Delta u & \displaystyle \frac{\partial x}{\partial v} \Delta v \\[8pt] \displaystyle \frac{\partial y}{\partial u} \Delta u & \displaystyle \frac{\partial y}{\partial v} \Delta v\\[6pt] \end{array} \right| = \left| \begin{array}{c@{\quad}c} \\[-10pt] \displaystyle \frac{\partial x}{\partial u} & \displaystyle \frac{\partial x}{\partial v} \\[8pt] \displaystyle \frac{\partial y}{\partial u} & \displaystyle \frac{\partial y}{\partial v} \\[6pt] \end{array} \right| \Delta u\,\Delta v = \frac{\partial (x,y)}{ \partial (u,v)} \Delta u\ \Delta v \] evaluated at \((u_0,v_0)\).
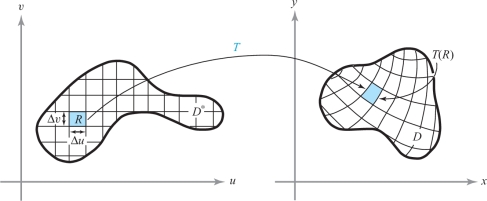
This fact and a partitioning argument should make formula (3) plausible. Indeed, if we partition \(D^*\) into small rectangles with sides of length \(\Delta u\) and \(\Delta v\), the images of these rectangles are approximated by parallelograms with sides \({\bf T}_u\, \Delta u\) and \({\bf T}_v\, \Delta v\), and hence with area \(| \partial (x,y) / \partial (u,v)|\, \Delta u\, \Delta v\). Thus, the area of \(D^*\) is approximately \(\sum \Delta u\, \Delta v\), where the sum is taken over all the rectangles \(R\) inside \(D^*\) (see Figure 16.9). Hence, the area of \(T (D^*)\) is approximately the sum \(\sum | \partial (x,y) / \partial (u,v) | \Delta u \,\Delta v\). In the limit, this sum becomes \[ \intop\!\!\!\intop\nolimits_{D^*} \left|\frac{\partial (x,y)}{\partial (u,v)} \right| {\,d} u{\,d} v. \]
Let us give another informal argument for the special case (4) of formula (3); that is, the case of polar coordinates. Consider a region \(D\) in the \(xy\) plane and a grid corresponding to a partition of the \(r\) and \(\theta\) variables (Figure 16.10). The area of the shaded region shown is approximately \((\Delta r) (r_{jk}\, \Delta \theta)\), because the arc length of a segment of a circle of radius \(r\) subtending an angle \(\phi\) is \(r \phi\). The total area is then the limit of \(\sum r_{jk}\, \Delta r \Delta \theta\); that is, \({\intop\!\!\intop}_{D^*} r{\,d} r{\,d} \theta\). The key idea is thus that the \(jk\)th “polar rectangle” in the grid has area approximately equal to \(r_{jk}\, \Delta r\, \Delta \theta\). (For \(n\) large, the \(jk\)th polar rectangle will look like a rectangle with sides of lengths \(r_{jk}\, \Delta \theta\) and \(\Delta r\).) This should provide some insight into why we say the “area element \(d x \,d y\)” is transformed into the “area element \(r d r\, d\theta\).”
318
example 2
Let the elementary region \(D\) in the \(xy\) plane be bounded by the graph of a polar equation \(r = f (\theta)\), where \(\theta_0 \le \theta \le \theta_1\) and \(f ( \theta) \ge 0\) (see Figure 16.11). In the \(r \theta\) plane we consider the \(r\)-simple region \(D^*\), where \(\theta_0 \le \theta \le \theta_1\) and \(0 \le r \le f ( \theta)\). Under the transformation \(x =r \cos \theta, y = r\sin \theta\), the region \(D^*\) is carried onto the region \(D\). Use equation (4) to calculate the area of \(D\).
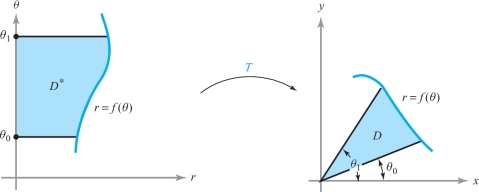
solution \begin{eqnarray*} A (D) = \intop\!\!\!\intop\nolimits_{D} {\it dx}\,{\it dy} & = & \intop\!\!\!\intop\nolimits_{D^*} \left| \frac{\partial (x,y)}{\partial (r, \theta)} \right| {\,d} r{\,d} \theta \\[4pt] & = & \intop\!\!\!\intop\nolimits_{D^*} r{\,d} r{\,d} \theta = \int_{\theta_0}^{\theta_1} \left[ \int_0^{f(\theta)} r{\,d} r \right] {\,d} \theta \\[2pt] & = & \int_{\theta_0}^{\theta_1} \left[ \frac{r^2}{2} \right]_0^{f(\theta)} d \theta = \int_{\theta_0}^{\theta_1} \frac{[f ( \theta)]^2}{2} d \theta \end{eqnarray*}
This formula for \(A(D)\) should be familiar from one-variable calculus.
Question 16.24 Section 16.2 Progress Check Question 2
3GdrTh9jOnR3ShVKMYewJ5K0+rdFxzAd6b57vAmTjtrak5/+v+BalXPrGhvKcivl2YcbaEWplU/N/46YRP5eyNAmBc83qh4RcR1ugAa4KqDgq5KQ1BSoaQrNtToo/njypyMBRlGwO9hfStprOeQ9kfoDYvSPmO04Q/XI2AG2xMbLpDtAw195Yx89q5dJifAKVUBbiXO8b9IxcQwPjL24bFPUoQAuIAISUDx0ZYLh44lvvnZ02IWGQy4M5B6j39PYoPF4dZsNt/rIWEjimBCgV+33zWfVMBq1jctclIoqOLPfGw9L5fh9MvutddCoTnlygm4zPA3BgxebFto4C2VA4bwO7t4+O3z0r+rbmeXMfSlKSPhZieaDaV1NZe8kOhVlcx+CeJLDJ73r2svVFjUi5MZlL9WhVjTbXGd0z7+4kbfg9nHuAjTPWaQ0hRZdR1tNJEoN1t4fuG6hkeMxawwQ/lB50LI2SJ5FTA99Bxi2Mr3FVmJ021YuGuFbwIAvjvYmv8W27x/PodlQiX+OqNtr2rAe3RSm7oXlGcR6dl+Flwq4YB36V6/IqVGMRbq+hjmFKBVetfwVB7Jk7ONJ/SWDFGKx9yZwizAm2UzkWZJZxtuEn4fD+asx/TW39dS1oaguAIefvIHAAfnjlq31w+3GNCGFMUEuSyv1/g+vWGTdDTZuwjL/+/edbsLGqTgjZWCNEtEWfiwJAHChj5w3SOimvfLY66LPFz11HhEpRCvUWE2hXHoTy/GG1fB4YGopAlpcFzoFCBNNPYp3gFS5FbkvkLoLhlyuVEMznDwWXyOSr3M=Change of Variables Formula
Before stating the two-variable change of variables formula, which is the culmination of this discussion, let us recall the corresponding theorem from one-variable calculus that goes under the name the method of substitution: \begin{equation} \int_a^b f (x(u)) \frac{{\it dx}}{{\,d} u} {\,d} u= \int_{x(a)}^{x(b)} f (x)\, {\it dx}, \end{equation} where \(f\) is continuous and \(u \mapsto x (u)\) is continuously differentiable on \([a,b]\).
319
proof
Let \(F\) be an antiderivative of \(f\); that is, \(F' =f\), whose existence is guaranteed by the fundamental theorem of calculus. The right-hand side of equation (5) becomes \[ \int_{x(a)}^{x(b)} f (x)\, {\it dx} =F (x(b)) - F (x(a)). \]
To evaluate the left-hand side of equation (5), let \(G (u) = F(x(u))\). By the chain rule, \(G' (u) = F' (x(u)) x' (u) = f (x(u)) x' (u)\). Hence, again by the fundamental theorem, \[ \int_a^b f (x (u)) x'(u) {\,d} u = \int_a^b G' (u) {\,d} u = G (b) - G (a) = F (x(b)) - F(x(a)), \] as required.
Suppose now that we have a \(C^1\) function \(u \mapsto x (u)\) that is one-to-one on \([a,b]\). Thus, we must have either \({\it dx}{/}{\,d} u \ge 0\) on \([a,b]\) or \({\it dx}{/}d u \le 0\) on \([a,b]\).footnote # Let \(I^*\) denote the interval \([a,b]\), and let \(I\) denote the closed interval with endpoints \(x (a)\) and \(x(b)\). (Thus, \(I = [x (a), x(b)]\) if \(u \mapsto x(u)\) is increasing and \(I = [ x(b) , x(a) ]\) if \(u \mapsto x(u)\) is decreasing.) With these conventions we can rewrite formula (5) as \[ \int_{I^*} f (x(u)) \left| \frac{{\it dx}}{{\,d} u} \right| {\,d} u = \int_I f (x)\, {\it dx}. \]
This formula generalizes to double integrals, as was already given informally in formula (3): \(I^*\) becomes \(D^*,I\) becomes \(D\), and \(|d x / d u|\) is replaced by \(|\partial (x,y) / \partial (u,v)|\). Let us state the result formally (the technical proof is omitted).
Theorem 2 Change of Variables: Double Integrals
Let \(D\) and \(D^*\) be elementary regions in the plane and let \(T \colon\, D^* \to D\) be of class \(C^1;\) suppose that \(T\) is one-to-one on \(D^*.\) Furthermore, suppose that \(D = T (D^*).\) Then for any integrable function \(f \colon\, D \to {\mathbb R},\) we have \begin{equation} \intop\!\!\!\intop\nolimits_{D} f (x,y)\, {\it dx}\,{\it dy}= \intop\!\!\!\intop\nolimits_{D^*} f (x(u,v), y(u,v)) \left| \frac{\partial (x,y)}{\partial (u,v)} \right| {\,d} u{\,d} v. \end{equation}
One of the purposes of the change of variables theorem is to supply a method by which some double integrals can be simplified. We might encounter an integral \(\intop\!\!\intop\nolimits_D f {\,d}\! A\) for which either the integrand \(f\) or the region \(D\) is complicated and for which direct evaluation is difficult. Therefore, a mapping \(T\) is chosen so that the integral is easier to evaluate with the new integrand \(f \,{\circ}\, T\) and with the new region \(D^*\) [defined by \(T ( D^*) = D\)]. Unfortunately, the problem may actually become more complicated if \(T\) is not selected carefully.
320
example 3
Let \(P\) be the parallelogram bounded by \(y = 2x, y=2x\,{-}\,2, y=x\), and \(y = x+1\) (see Figure 16.12). Evaluate \({\intop\!\!\intop}_P xy\, {\it dx}\, {\it dy}\) by making the change of variables \[ x=u -v, y=2u -v, \] that is, \(T (u,v) = (u-v, 2u-v).\)
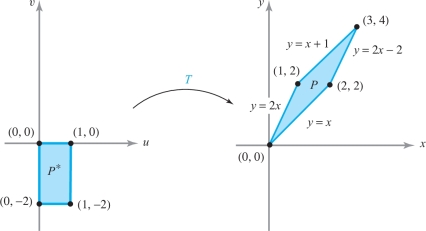
solution The transformation \(T\) has nonzero determinant and so is one-to-one (see Exercise 12, Section 16.1). It is designed so that it takes the rectangle \(P^*\) bounded by \(v=0, v=-2, u=0, u=1\) onto \(P\). The use of \(T\) simplifies the region of integration from \(P\) to \(P^*\). Moreover, \[ \left| \frac{\partial (x,y)}{\partial (u,v)} \right| = \left| \hbox{ det}\left[ \begin{array}{c@{\quad}c} 1 & -1 \\ 2 & -1 \end{array} \right] \right| =1. \]
Therefore, by the change of variables formula, \begin{eqnarray*} \intop\!\!\!\intop\nolimits_{P} xy\,{\it dx}\,{\it dy} & =& \displaystyle \intop\!\!\!\intop\nolimits_{P^*} (u-v) (2u-v) {\,d} u{\,d} v = \int_{-2}^0 \int_0^1 (2 u^2 - 3vu + v^2) {\,d} u {\,d} v \\[3pt] & = & \int_{-2}^0 \left[\frac{2}{3} u^3 - \frac{3 u^2 v}{2}+ v^2 u \right]^1_0 {\,d} v = \int_{-2}^0 \left[ \frac{2}{3} - \frac{3}{2} v + v^2 \right] {\,d} v \\[3pt] &= & \left[ \frac{2}{3} v - \frac{3}{4} v^2+ \frac{v^3}{3} \right]_{-2}^0 = {-}\!\left[ \frac{2}{3} (-2) -3 - \frac{8}{3} \right] \\[3pt] & =& {-}\!\left[ - \frac{12}{3} -3 \right] = 7. \\[-30pt] \end{eqnarray*}
Question 16.25 Section 16.2 Progress Check Question 3
EvtUy1CZWvY0ehSF3ScQWXBjkc/V7X+y4g9WwS+40FPhUbqTtaE8/jfKkLPVHBNaZ0qSVtoJMTuw92CEEJp/W4KBPwNVId7N5UJEGlna0VPj7zsMzRmkvSATWh3+UJOrrytKMM6vsbgA5dPtP18MmIsEF3UultcG97KAnSdoPsn//JKUJxPddQPllmmxutoD4z1L/4l2JAfReLhFtH64XmdK/s6JpalofQsapL0HsIK2Vah49B8gQJWFlw2R8UEzN5hMeubY14DkyOf4VSynN3KPTw58hNsL5rnLfh1VDuyYyEeMyURXwWmPfhhSdYwhvhyz5NfdSYC7B/ND0FSXgAjn1W1k0pOg02OBo+sVaG6IT3rFCrMkODcdi/+4il1izkaPDuAL6uiHdi/NOIz3aGxgjnLGw3XuW1rcjS8Fp32uA2zalIaSgNlRipO/F2yCVHyIGy+xakVuL5UPLprdwKgg00x/D2kn6u+MkWYtg///j6HmRfBLzM+DJJ7rm7+DQeyeC3du6zPJDZQdEGOgw+V4k6dtp7SPaVfxs9sAvRt78yixXN7Zq5nGBS1YltFpyNHgjrCoXYCL2WgEv2BImjTCM5YXLOyfQNV6fMIlsSVb5VZcJ6TAXw1qVPHprwEDNaGH3aayHK88okPTp4Huy6GXZuu4V/nriroGiWbLT/ovMu9CZpcA3Zww3MY4N+5HbLYvqMIHk/GKEaVqupKanwVETPBcBSwhwRsDV/RaX/eejkQcDvvhmkwMKLe/oSvKcYv5dq2xSfZvLAPIVuWGIOWzoP09jLaJnxLH/cjYE2NCoWuGRumhgj5k0EjqWinFk3LBwK7g6HGj0jpsg8+uUVSutne8pjM40gyxj7j0mXPrXYg0PW8wHN50qOx1EBgWSTti+LgVu0Pb+FCQWOGATIPVatg1P0gMbgWSFGWgOAH9cPq0ztVasrcoOH7qDwfw3B5sV552fje3wsBUC5elczDXorwev3fDHQUFlE5Bv2DrR4F2lSnBuk3Tewqq3kqvOlH3BvPriJJ1Of1DeK71IeMm1HhbzsZtmIdg/YCSopQGSUwU1s/NCIiAquGhKykg0GaRF2PT3WU1iG3ebJNcHUM4CDqGOHIlF30twMGnHRcHo4+H3Rn/igdE7n4FoIAbWyK93J2ij0GeHrLEJtwsLeu8MSDV5kShmqkGFMoD8dRR+YkaRbaR4ZuO6l25fT5Uwoab9aLsjbDc/CMxZHP7eA1N/SBqZMh6Jt+z9BvkNLjW8HuAFQMoDakqZb2SSm9IjewjhBQQGSK3JXFcrv+XrIDtiRU+6xUkjUNrB+FyLuFML3+2pB4rb2czavzYTcIvIO4tiBk0kz2mMQ7RBrPPqFeu1z2KEIZMjA5xJujDeCuiBDTHV9G3geQBypIhf7ymS2Hqxs3Rw/1QArJsrpaaL41QpycFJ3lGvMzyk0NO7+Wcl63Oo8PMHIidqgQZkSxKm5d8vOUheHL82Xr/kb87U4pKWZ1r7EKjHyHIt6zhQEnU6lAOSJmObBsCkSlpZU7e55Dw3X+yGGtBziSrOPCE7nCfflMQACItIYlXXK0BZVPYO7QM0CJmGVvfjaZuKh+H61pI7HtYpAA1YOF4GOhAe3vDk9RzT5QhYukLlNuq/vaeFluKcjhz5W14sEA=Integrals in Polar Coordinates
Suppose we consider the rectangle \(D^*\) defined by \(0 \le \theta \le 2 \pi, 0 \le r \le a\) in the \(r \theta\) plane. The transformation \(T\) given by \(T (r,\theta) = (r \cos \theta, r \sin \theta)\) takes \(D^*\) onto the disk \(D\) with equation \(x^2 + y^2 \le a^2\) in the \(xy\) plane. This transformation represents the change from Cartesian coordinates to polar coordinates. However, \(T\) does not satisfy the requirements of the change of variables theorem, because it is not one-to-one on \(D^*\): In particular, \(T\) sends all points with \(r=0\) to \((0, 0)\) (see Figure 16.13 and Example 3 of Section 16.1). Nevertheless, the change of variables theorem is valid in this case. Basically, the reason for this is that the set of points where \(T\) is not one-to-one lies on an edge of \(D^*\), which is the graph of a smooth curve and therefore, for the purpose of integration, can be neglected. In summary, the formula is valid when \(T\) sends \(D^*\) onto \(D\) in a one-to-one fashion, except possibly for points on the boundary of \(D^*\).
321
Change of Variables—Polar Coordinates
\begin{equation} \intop\!\!\!\intop\nolimits_{D} f (x,y)\, {\it dx}\,{\it dy}= \intop\!\!\!\intop\nolimits_{D^*} f (r \cos \theta, r \sin \theta)\, r{\,d} r {\,d} \theta \end{equation}
example 4
Evaluate \(\intop\!\!\intop\nolimits_{\! D} \log\, (x^2 + y^2)\, {\it dx}\,{\it dy}\), where \(D\) is the region in the first quadrant lying between the arcs of the circles \(x^2 + y^2 =a^2\) and \(x^2 + y^2 =b^2,\) where \(0<a<b\) (Figure 16.14).
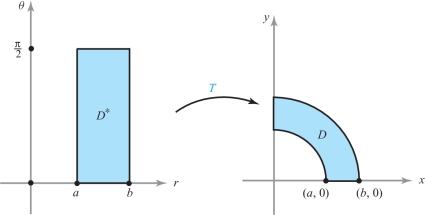
solution These circles have the simple equations \(r=a\) and \(r=b\) in polar coordinates. Moreover, \(r^2 = x^2 + y^2\) appears in the integrand. Thus, a change to polar coordinates will simplify both the integrand and the region of integration. From Example 7, Section 16.1, the polar coordinate transformation \[ x =r \cos \theta, y = r \sin \theta \] sends the rectangle \(D^*\) given by \(a \le r \le b, 0 \le \theta \le \pi/2\) onto the region \(D\). This transformation is one-to-one on \(D^*\) and so, by formula (7), we have \begin{eqnarray*} \intop\!\!\!\intop\nolimits_{D} \log\, (x^2 + y^2)\, {\it dx}\,{\it dy} &=&\int_a^b \int_0^{\pi/2}r \log r^2 {\,d} \theta {\,d} r \\[6pt] &= &\frac{\pi}{2} \int_a^b r \log r^2 {\,d} r = \frac{\pi}{2}\int_a^b 2r \log r {\,d} r. \end{eqnarray*}
322
Applying integration by parts, or using the formula \[ \int x \log x{\it {\,d} x} = \frac{x^2}{2} \log x - \frac{x^2}{4} \] from the table of integrals at the back of the book, we obtain the result \[ \frac{\pi}{2} \int_a^b 2r \log r{\,d} r = \frac{\pi}{2} \left[ b^2 \log b - a^2 \log a - \frac{1}{2} (b^2 - a^2) \right]. \]
Question 16.26 Section 16.2 Progress Check Question #4
wLuAxkcIPb7Fn24zCcrwLZnvj7OThe9Ws0FmLyqaCYfwnRH+7zFu8bEQioq+nlYQ2mO59QGJT/WHj70+iY8Z0qckIH698xi8GD4ODVNI9DputNlguhLkMTlpsVf1NmOSeLxs2S6rMXE3k7YGjAs+rm7SLuzYBQXM2LVYdN3cy5NWNadZrMXjoPHds34+yKsxaX7yrMcPETPPwl0GnzIGKWOnkuHWmuZpvbfYthvoiQWUc70pouRHRT3q5slPVuJIWhlqyf/7CmVC8gFMPdwcKMDwsQ46QQ1j3XsBuhW29uWLHNFXzJWltPjG1gGG3fgUP7jSaSxStIW/TSY+eYiUlgG97hLNnIJh8zBT60FobQXJ5ijD0DD4o8sVkZtD05a3OybEWsg+gjnZeOMQI7W7MVPjaKayVhuemNBdIPfhaPDc7AUnO2SY4hb4SHjDY0fo0rXWr9YcSlctdilqrC0AlFm0ytI0E1ohHkN6pEoDVJAfdE8pFfH7vtHVa6oM4LfuRQ2AJchuHg0=example 5
The Gaussian Integral One of the most beautiful applications of the change of variables formula, polar coordinates, and the reduction to iterated integrals is their application to the following formula, known as the Gaussian integral: \[ \int^\infty_{-\infty}e^{-x^{2}}dx = \sqrt\pi. \]
Not only is this formula very attractive in its own right, but it is also useful in areas such as statistics. It also illustrates the unity of the transcendental numbers \(e\) and \(\pi\) nearly as well as does the classic formula \(e^{i\pi } = -1\).
To carry out the integration of the Gaussian integral,footnote # we first evaluate the double integral \[ \intop\!\!\!\intop\nolimits_{D_{a}} e^{-(x^2 + y^2)} {\it dx}\, {\it dy}, \] where \(D_{a}\) is the disk \(x^{2}+y^{2} \le a^{2}\). Because \(r^{2} = x^{2}+y^{2}\), and \({\it dx}\, {\it dy} = r\, dr\, d \theta \), the change of variables formula gives \begin{eqnarray*} \intop\!\!\!\intop\nolimits_{D_a} e^{-(x^2 + y^2)} {\it dx}\, {\it dy} &=& \int^{2\pi}_0 \int^a_0 e^{-r^2} r {\,d} r {\,d} \theta = \int^{2\pi}_0 \left.\left(-\frac{1}{2}e^{-r^2} \right)\right|^a_0 d\theta\\[6pt] &=& -\frac{1}{2} \int^{2\pi}_0 (e^{-a^2}-1)\ d\theta = \pi (1-e^{-a^2}).\\[-29.5pt] \end{eqnarray*}
323
If we let \(a \to \infty\) in this expression, we give meaning to the improper integral and get \[ \intop\!\!\!\intop\nolimits_{{\mathbb R}^2} e^{-(x^2 + y^2)} {\it dx}\, {\it dy} = \pi. \]
Instead of using the disks \(D_{a}\), we can also evaluate this improper integral as the limit of the integrals over the rectangles \(R_{a} = [- a, a ] \times [- a, a]\) as \(a \to \infty \), and in doing so we get \[ \lim_{a\rightarrow \infty} \intop\!\!\!\intop\nolimits_{R_a} e^{-(x^2 + y^2)} {\it dx}\, {\it dy}. \]
Assuming that \[ \lim_{a \rightarrow \infty } \int\!\!\!\int_{D_{a}} e^{-(x^2+y^2)} dx \,dy = \lim_{a \rightarrow \infty } \int\!\!\!\int_{R_{a}}e^{-(x^2+y^2)} dx\, dy, \]
To see a proof of this fact, click here.
\(\bf Proof\) of the equality of the following two limits \[ \lim_{a \rightarrow \infty } \int\!\!\!\int_{D_{a}} e^{-(x^2+y^2)} dx \,dy = \lim_{a \rightarrow \infty } \int\!\!\!\int_{R_{a}}e^{-(x^2+y^2)} dx\, dy, \]
In the text above, we showed that \[ \lim_{a \rightarrow \infty } \int\!\!\int_{D_{a}} e^{-(x^2+y^2)} dx \,dy \] exists by directly evaluating it. Thus, it suffices to show that \[ \lim_{a \rightarrow \infty} \left( \int\!\!\!\int_{R_{a}} e^{-(x^2+y^2)} dx\, dy - \int\!\!\! \int_{D_{a}} e^{-(x^2+y^2)} dx \,dy \right)\] equals zero. The limit equals \[ \lim_{a \rightarrow \infty } \int\!\!\int_{C_{a}} e^{-(x^2+y^2)} dx\, dy ,\] where \( C_a \) is the region between \( R_a\) and \( D_a\) (see the Figure below).
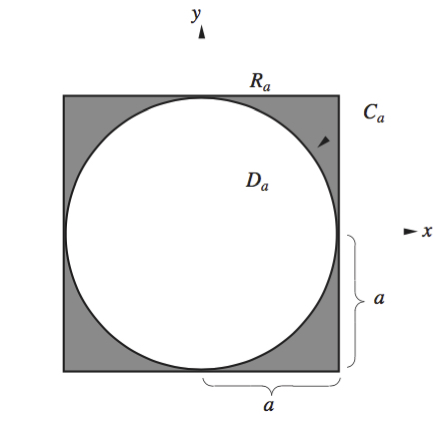
In the region \( C_a, \sqrt{x^2 + y^2} \geq a \) (the radius of \( D_a),\) so \( e^{-(x^2+y^2)} \leq e^{-a^{2}} .\) Thus, \[ 0 \leq \int\!\!\int _{C_{a}} e^{-(x^2+y^2)} dx \,dy \leq \int\!\!\int _{C_{a}} e^{-a^{2}} dx \,dy\] \[ = e^{-a_{2}} \,\,{\rm area} \,\, (C_a) = e^{-a^{2}} (4a^2 - \pi a^2) = (4 - \pi )a^2e^{-a^{2}} .\] Thus it is enough to show that \(\lim_{a \rightarrow \infty} a^2 e^{-a^{2}} = 0. \) But, by l'H\(\hat{{\rm o}}\)pital's rule \[ \lim_{a \rightarrow \infty} a^2 e^{-a^{2}} = \lim_{a \rightarrow \infty} \left(\frac{a^2}{e^{a^{2}}} \right) = \lim_{a \rightarrow \infty} \left(\frac{2a}{2 a e^{a^{2}}} \right) = \lim_{a \rightarrow \infty} \frac{1}{e^{a^{2}}} = 0, \] as required. \( \Box\)
we then obtain \[ \lim_{a\rightarrow \infty} \intop\!\!\!\intop\nolimits_{R_a} e^{-(x^2 + y^2)} {\it dx}\, {\it dy} =\pi. \]
By reduction to iterated integrals, we can write this as \[ \lim_{a\rightarrow \infty} \left[\int^a_{-a} e^{-x^2} {\it dx}\, \int^a_{-a} e^{-y^2} {\it dy} \right] =\left[\lim_{a\rightarrow \infty}\int^a_{-a}e^{-x^2} {\it dx}\, \right]^2 =\pi . \]
That is, \[ \left[\int^\infty_{-\infty} e^{-x^2} {\it dx}\right]^2 = \pi. \]
Thus, taking square roots, we arrive at the desired result.
Here is a variant of the Gaussian integral. Evaluate \[ \int^\infty_{-\infty} e^{-2x^2} {\it dx}. \]
To do this, use the change of variables formula \(y=\sqrt{2}x\) to reduce the problem to the Gaussian integral just computed: \begin{eqnarray*} \int^\infty_{-\infty} e^{-2x^2} {\it dx} &=& \lim_{a \rightarrow \infty} \int^a_{-a} e^{-2x^2} {\it dx}= \lim_{a\rightarrow \infty}\int^{\sqrt{2}a}_{-\sqrt{2}a} e^{{-y^2}} \frac{{\it dy}}{\sqrt{2}} \\[3pt] &=& \frac{1}{\sqrt{2}} \int^\infty_{-\infty} e^{-y^2} {\it dy} = \frac{1}{\sqrt{2}}\sqrt{\pi} = \sqrt{\frac{\pi}{2}.}\\[-29pt] \end{eqnarray*}
To see another challenging example using polar coordinates, click here.
\(\bf example\)
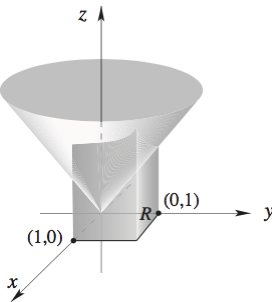
Evaluate \[ \int \!\!\! \int_R \sqrt{x^2 + y^2} dxdy, \] where \(R = [0,1] \times [0,1]\).
\(\bf solution\) This double integral is equal to the volume of the region under the graph of the function \[ f (x,y) = \sqrt{x^2 + y^2} \] over the rectangle \(R = [0,1] \times [0,1]\); that is, it equals the volume of the three-dimensional region shown here:
As it stands, this integral is difficult to evaluate. Since the integrand is a simple function of \(r^2 = x^2 + y^2\), we might try a change of variables to polar coordinates. This will result in a simplification of the integrand but, unfortunately, not in the domain of the integration. However, the simplification is sufficient to enable us to evaluate the integral. To apply Theorem 2 of the text with polar coordinates, refer to this Figure:
The reader can verify that \(R\) is the image under \(T(r,\theta) = (r \cos \theta, r \sin \theta)\) of the region \(D^{*} = D_1^{*} \cup D_2^{*}\) where for \(D_1^{*}\) we have \(0 \leq \theta \leq \frac{1}{4} \pi\) and \(0 \leq r \leq \sec \theta\); for \(D_2^{*}\) we have \(\frac{1}{4} \pi \leq \theta \leq \frac{1}{2} \pi\) and \(0 \leq r \leq \csc \theta\). The transformation \(T\) sends \(D_1^{*}\) onto a triangle \(T_1\) and \(D_2^{*}\) onto a triangle \(T_2\). The transformation \(T\) is one-to-one except when \(r=0\), and so we can apply Theorem 2. From the symmetry of \(z = \sqrt{x^2 + y^2}\) on \(R\), we can see that \[ \int \!\!\! \int_R \sqrt{x^2 + y^2}\ dxdy=2 \int \!\!\! \int_{T_1} \sqrt{x^2 + y^2}\ dxdy. \] Changing to polar coordinates, we obtain \[ \int \!\!\! \int_{T_1} \sqrt{x^2 + y^2}\ dxdy= \int \!\!\! \int_{D_1^{*}} \sqrt{r^2} r\ drd \theta = \int \!\!\! \int_{D_1^{*}} r^2\ drd \theta. \] Next we use iterated integration to obtain \[ \int \!\!\! \int_{D_1^{*}} r^2\ drd \theta = \int_0^{ \pi/4} \biggl[ \int_0^{ \sec \theta} r^2\ dr \biggr] d\theta = \frac {1}{3} \int_0^{ \pi/4} \sec^3 \theta\ d\theta. \] Consulting a table of integrals (or calculating this integral directly using integration by parts) to find \(\int \sec^3 x\ dx\), we have \[ \int_0^{ \pi/4} \sec^3 \theta\ d\theta = \biggl[ \frac {\sec \theta \tan \theta} {2} \biggr]_0^{ \pi/4} + \frac{1}{2} \int_0^{\pi/4} \sec \theta\ d\theta = \frac {\sqrt{2}}{2} + \frac{1}{2} \int_0^{\pi/4} \sec^3 \theta\ d\theta. \] Consulting the table again for \(\int \sec x\ dx\), we find \[ \frac{1}{2} \int_0^{\pi/4} \sec \theta\ d\theta = \frac{1}{2} [ \log | \sec \theta + \tan \theta |]_0^{\pi/4} = \frac{1}{2} \log ( 1 + \sqrt{2} ). \] Combining these results and recalling the factor \(\frac{1}{3}\), we obtain \[ \int \!\!\! \int_{D_1^{*}} r^2\ drd\theta = \frac{1}{3} \biggl[ \frac{\sqrt{2}} {2} + \frac{1}{2} \log (1 + \sqrt{2}) \biggr] = \frac{1}{6} [ \sqrt{2} + \log (1 + \sqrt{2})]. \] Multiplying by 2, we obtain the answer % \begin{equation} \int \!\!\! \int_R \sqrt {x^2 + y^2}\ dxdy= \frac{1}{3} [ \sqrt{2} + \log (1 + \sqrt{2})]. \ \ \ \ \ \blacklozenge \end{equation} Instead of using the substitution \(T\), one can alternatively divide the original square into two triangles \(T_1\) and \(T_2\) as in the text, write the integral over \(T_1\) as a double integral (first with respect to \(y\), then with respect to \(x\)); in the integral over \(y\), substitute \(y = xv\), then use a standard integral from a table of integrals.
Change of Variables Formula for Triple Integrals
To state this formula, we first define the Jacobian of a transformation from \({\mathbb R}^3\) to \({\mathbb R}^3\)—it is a simple extension of the two-variable case.
Definition
Let \(T \colon\, \,W \subset {\mathbb R}^3 \to {\mathbb R}^3\) be a \(C^1\) function defined by the equations \(x=x(u,v,w), y=y(u,v,w), z= z(u,v,w)\). Then the Jacobian of \(T\), which is denoted \(\partial (x,y,z) / \partial (u,v,w)\), is the determinant \[ \left| \begin{array}{c@{\quad}c@{\quad}c} \\[-8pt] \displaystyle \frac{\partial x}{\partial u} & \displaystyle \frac{\partial x}{\partial v} & \displaystyle \frac{\partial x}{\partial w} \\[9pt] \displaystyle \frac{\partial y}{\partial u} & \displaystyle \frac{\partial y}{\partial v} & \displaystyle \frac{\partial y}{\partial w}\\[9pt] \displaystyle \frac{\partial z}{\partial u} & \displaystyle \frac{\partial z}{\partial v} & \displaystyle \frac{\partial z}{\partial w}\\[6pt] \end{array} \right|. \]
324
The absolute value of this determinant is equal to the volume of the parallelepiped determined by the three vectors \begin{eqnarray*} {\bf T}_u &=& \frac{\partial x}{\partial u} {\bf i} + \frac{\partial y}{\partial u} {\bf j} + \frac{\partial z}{\partial u} {\bf k}, \\[4pt] {\bf T}_v &=& \frac{\partial x}{\partial v} {\bf i} + \frac{\partial y}{\partial v} {\bf j} + \frac{\partial z}{\partial v} {\bf k}, \\[4pt] {\bf T}_w &=& \frac{\partial x}{\partial w} {\bf i} + \frac{\partial y}{\partial w} {\bf j} + \frac{\partial z}{\partial w} {\bf k}. \end{eqnarray*}
Just as in the two-variable case, the Jacobian measures how the transformation \(T\) distorts the volume of its domain. Hence, for volume (triple) integrals, the change of variables formula takes the following form:
Change of Variables Formula: Triple Integrals
\begin{equation} \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} f (x,y,z)\, {\it dx}\,{\it dy}\,{\it dz} \\[5pt] \quad= \intop\!\!\!\intop\!\!\!\intop\nolimits_{W^*} f(x (u,v,w), y(u,v,w), z(u,v,w)) \left|\frac{\partial (x,y,z)}{\partial (u,v,w)} \right| {\,d} u{\,d} v{\,d} w, \end{equation} where \(W^*\) is an elementary region in \(uvw\) space corresponding to \(W\) in \(xyz\) space, under a mapping \(T \colon\, (u,v,w) \mapsto (x(u,v,w), y(u,v,w) , z(u,v,w))\), provided \(T\) is of class \(C^1\) and is one-to-one, except possibly on a set that is the union of graphs of functions of two variables.
Cylindrical Coordinates
Let us apply formula (8) to cylindrical and then to spherical coordinates. First, we compute the Jacobian for the map defining the change to cylindrical coordinates. Because \[ x =r \cos \theta, y = r \sin \theta, z=z, \] we have \[ \frac{\partial (x,y,z)}{\partial (r, \theta,z)} = \left|\begin{array}{c@{\quad}c@{\quad}c} \cos \theta & - r \sin \theta & 0 \\[.5pt] \sin \theta & \hphantom{-} r \cos \theta & 0 \\[.5pt] 0 & 0 & 1 \end{array} \right| =r. \]
Thus, we obtain the formula
Change of Variables—Cylindrical Coordinates
\begin{equation} \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} f (x,y,z)\, {\it dx}\,{\it dy}\,{\it dz} = \intop\!\!\!\intop\!\!\!\intop\nolimits_{W^*} f (r \cos\theta, r \sin \theta, z)\,r{\,d} r{\,d} \theta\, {\it dz}. \end{equation}
Spherical Coordinates
325
Next we consider the spherical coordinate system. Recall that it is given by \[ x = \rho \sin \phi \cos \theta, y = \rho \sin \phi \sin \theta, z= \rho \cos \phi. \]
Therefore, we have \[ \frac{\partial (x,y,z)}{\partial (\rho, \theta,\phi)} = \left| \begin{array}{c@{\quad}c@{\quad}c} \sin \phi \cos \theta & - \rho \sin \phi \sin \theta & \rho \cos \phi \cos \theta \\ \sin \phi \sin \theta &\rho \sin \phi \cos \theta & \rho \cos \phi \sin \theta \\ \cos \phi & 0 &- \rho \sin \phi \end{array} \right|. \]
Expanding along the last row, we get \begin{eqnarray*} \frac{\partial (x,y,z)}{ \partial ( \rho, \theta, \phi)} & = & \cos \phi \!\left| \begin{array}{r@{\quad}r} - \rho \sin \phi \sin \theta & \rho \cos \phi \cos \theta \\ \rho \sin \phi \cos \theta & \rho \cos \phi \sin \theta \end{array} \right| \\[6pt] && {-} \rho \sin \phi\!\left| \begin{array}{r@{\quad}r} \sin \phi \cos \theta & - \rho \sin \phi \sin \theta \\ \sin \phi \sin \theta & \rho \sin \phi \cos \theta \end{array} \right| \\[6pt] & = & - \rho^2 \cos^2 \phi \sin \phi \sin^2 \theta - \rho^2 \cos^2 \phi \sin \phi \cos^2 \theta \\[2pt] && {-} \rho^2 \sin^3 \phi \cos^2 \theta - \rho^2 \sin^3 \phi \sin^2 \theta \\[2pt] & = & - \rho^2 \cos^2 \phi \sin \phi - \rho^2 \sin^3 \phi = - \rho^2 \sin \phi. \end{eqnarray*}
Thus, we arrive at the formula:
Change of Variables—Spherical Coordinates
\begin{equation} \intop\!\!\!\intop\!\!\!\intop\nolimits_{ W} f (x,y,z)\, {\it dx}\,{\it dy}\,{\it dz}\\[6pt] =\intop\!\!\!\intop\!\!\!\intop\nolimits_{W^*} f ( \rho \sin \phi \cos \theta, \rho \sin \phi \sin \theta, \rho \cos \phi) \rho^2 \sin \phi\ {\,d} \rho{\,d} \theta{\,d} \phi. \end{equation}
To prove formula (10), we must show that the transformation \(S\) on the set \(W^*\) is one-to-one except on a set that is the union of finitely many graphs of continuous functions. We shall leave this verification as Exercise 34.
example 6
Evaluate \[ \displaystyle\int\!\!\!\int\!\!\!\int_W \exp\, (x^2 + y^2 + z^2)^{3/2} {\,d} V, \] where \(W\) is the unit ball in \({\mathbb R}^3\).
326
solution First note that we cannot easily integrate this function using iterated integrals (try it!). Hence (employing the strategy in the quote that opened this chapter), let us try a change of variables. The transformation into spherical coordinates seems appropriate, because then the entire quantity \(x^2 + y^2 + z^2\) can be replaced by one variable, namely, \(\rho^2\). If \(W^*\) is the region such that \[ 0 \le \rho \le 1,0 \le \theta \le 2 \pi , 0 \le \phi \le \pi, \] we can apply formula (10) and write \[ \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} \exp\, (x^2 + y^2 + z^2)^{3/2} {\,d} V = \intop\!\!\!\intop\!\!\!\intop\nolimits_{W^*} \rho^2 e^{\rho^3} \sin \phi{\,d} \rho{\,d} \theta{\,d} \phi. \]
This integral equals the iterated integral \begin{eqnarray*} \int_0^1 \int_0^{\pi} \int_0^{2 \pi} e^{\rho^3} \rho^2 \sin \phi{\,d} \theta{\,d} \phi{\,d} \rho & = & 2 \pi \int_0^1 \int_0^{\pi} e^{\rho^3} \rho^2 \sin \phi{\,d} \phi{\,d} \rho \\[5pt] &=& - 2 \pi \int_0^1 \rho^2 e^{\rho^3} [\cos \phi]_0^{\pi}{\,d} \rho \\[5pt] &=& 4 \pi \int_0^1 e^{\rho^3} \rho^2 {\,d} \rho = {\frac{4}{3}} \pi \int_0^1 e^{\rho^3} (3 \rho^2){\,d} \rho \\[5pt] & =& \left[{\frac{4}{3}} \pi e^{\rho^3}\right]_0^1= {\frac{4}{3}} \pi (e-1).\\[-28pt] \end{eqnarray*}
Question 16.27 Section 16.2 Progress Check Question #5
KbGDBveUTt3BKLg1DsrBpsC3SyExdDdcpP4Ghk6bNuS2b4PyV59WNWF4Wc1U0JFJUXNEU5Hyrw2PlUvY5aeHaFL29NJBlWvl2JvJWFoVdVWwGcDY1Q8QUM8JxqeOhjItpWNSyuo0DZxswObUviRV2IVpCX6a2Sv4w66IZeXoyiuyFf9QBbltHu7s9Ow3r2X6KX//JKd361j08zWpmsm86Jq7iFWy7KWULsf2Ts6W0fBnvzrz05bmceimgMy4Ulg+wQ+k8ZxNsMkYLzfcR6Z6geUHR2s1abqKPEDt8VmxfkXnUp9ZSxbRfPPqJ9SyypurAknW/J5pbx5y7EH2edG2ynzi7BjSwL+nHzSQeIEyvSBsEM4BEOjpFjelMWvl2CDSOmeGMP4acp7q+l/TpUamCxsa04TtOj8xE2vNXpHY5EaxnXry+ARgml4OLwIGjELH5bOzd9ZHTKkQDEIe7YwpBIdJ/ZG6wp4Zge9Pm4raJYsAY27PuZlVo/dVlSLr+NEUeutg/G8tzzFoiogiQ2BOnVnIum/LCNCUB2Miq/lgTgaFDJP2Lqd/9GcDNjQCTxuwe/zY727w2yBZxS3+nvd2cQ+4r6O8xzEWMkytMQufcFw+EfyzmI7MogcCpQOe5Y/PN2711YmRgEnMGKSEt6WBKJurHufKVrE9OzsaX/LaxLAtAan2Ji3Ea4hT5YnL/WH6fjZ7LGZUs7wWOwSOW+7GSbPTIzDZ9HKfAE/Y85UnVx3cjpwHsX3Yh5qsLz608Vy0cRhP3H24DkWm8PccMDBUP0FZ7/jlAEJWSRegOIMJxMUv1O6NScdhYab8O/gXouhnpb2+XCv/pXb+ngTDnoqP5BZvPpbH7KePgtYNGLY+NhfgBQILtKXdSIVh7PxqADnm9D3DcUY6kyuTMr5k3rU0y1Cehi1rmhoc6z18glEkGtsGc+t4TLQoj7npr2BLKuFFaxVDrbznJmjK1PHmIr0Ekc1w5GKt4AL9vtMgNooAqlgxXuJmtM+NaPhChU/usO+r8tWc2kj8GTWZxWraXhgD4GK9lIpCOpJeUSWS2Jb6o6/7sj0DnZaVxhWQwHNMipdYg48stB3J2JvVHBvOimhBbmqFQILp0S1JhT/x3x+3fk9rCh0TsLsnXIOyg2YrumJg2fydqYHDg8QR/kG/VPbxMD7S1Cx9oixJ3vgP3cVObQ3lJHqIjyjDGeFbEpBNOsaI1uqVovXbqeijBalCT5pC/5/sgPN1MB2Tb1TmKIwwhhcIykQStao86dUy7cIAzPMXxFjIab4o4jE+pAN5snRJjvaQIOLJQ7Sh/z2K4Eo/KR5xjxLBXVF2eO3W/dS2SbcsCsXYjtUQAo7hm2X//pAudK7AmoN09WAvI+/DHCfitc3W3MgMnpLfZx9T/r2qXjc/5Dw38b0lgsxQam8+07huAQ1FnjqplkAPbu2lNt14Lcuq77rTWPOjhKPZROKXytZRHAOaxAurD359aYGM52gsN8e99ZAp6BZaIWWIVhyU8ht5W6l57smotuMKEfAMspgb6bfaAQhjiADWHceizbMfcrKS9ntvL0W0j8JzwzfrVODNOYdVLcIdvaSoDbuaXNsQ1bPfegtKB9jDHNx3W0alYmjCdmHfrLyklc+DedSitULRDM6EKQsUq6LmVz6Cw089UuvzmL/c99SvAudbP5Hr8QcR36wJUziOrAb5GWq6Wd/2BeJegJeCo+MXHF1vyZxvIzrfTHepkJyY8ekWs94UhtLhBVeLqXrxkNKXdcZgW9rtSZkE40rWRMzrxp1h6z7oHuBoXhRlmNbtfPE87jeUS2OOazO9wcILA5S2e6LganyHdOJtHQysk8Y5e7i5A4zbkeOpQCJp79mw2NhMt7jFcEG6GtwM8cZ/BM7au73Ak4Q5vli4AJWROQmXO38QU2wVgMK0t1e7mlrNr2PCdlJy3SNmi2Stnpzwa+7kqG8cc3Q=example 7
Let \(W\) be the ball of radius \(R\) and center \((0, 0, 0)\) in \({\mathbb R}^3\). Find the volume of \(W\).
solution The volume of \(W\) is \({\intop\!\!\intop\!\!\intop}_W {\it dx}\, {\it dy}\, {\it dz}\). This integral may be evaluated by reducing it to iterated integrals or by regarding \(W\) as a volume of revolution, but let us evaluate it here by using spherical coordinates. We get \begin{eqnarray*} \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} {\it dx}\,{\it dy}\,{\it dz} & = & \int_0^{\pi} \int_0^{2 \pi} \int_0^R \rho^2 \sin \phi{\,d} \rho{\,d} \theta\ {\,d} \phi = \frac{R^3}{3} \int_0^{\pi} \int_0^{2 \pi} \sin \phi {\,d} \theta{\,d} \phi\\[5pt] & =& \frac{2 \pi R^3}{3} \int_0^\pi \sin \phi\ d \phi = \frac{2 \pi R^3}{3} \{- [\cos ( \pi) - \cos (0) ]\} = \frac{4 \pi R^3}{3},\\ \end{eqnarray*} which is the standard formula for the volume of a solid sphere.