16.3 Applications
329
In this section, we shall discuss average values, centers of mass, moments of inertia, and the gravitational potential as applications.
Averages
If \(x_1,\ldots ,x_n\) are \(n\) numbers, their average is defined by \[ [x_i]_{\rm av}=\frac{x_1 +\cdots+x_n}{n}=\frac{1}{n}\sum^n_{i=1}x_i. \]
Notice that if all the \(x_i\) happen to have a common value \(c\), then their average, of course, also equals \(c\).
This concept leads us to define the average values of functions as follows.
Average Values
The average value of a function of one variable on the interval \([a,b]\) is defined by \[ [f]_{\rm av}= \frac{\displaystyle\int^b_a f(x){\it {\,d} x}}{b-a}. \]
Likewise, for functions of two variables, the ratio of the integral to the area of \(D\), \begin{equation*} [f]_{\rm av}=\frac{\displaystyle\intop\!\!\!\intop\nolimits_{D} f(x,y){\it {\,d} x}\, {\it {\,d} y}}{\displaystyle\intop\!\!\!\intop\nolimits_{D} {\it dx}\, {\it dy}},\tag{1} \end{equation*} is called the average value of \(f\) over \(D\). Similarly, the average value of a function \(f\) on a region \(W\) in 3-space is defined by \[ [f]_{\rm av}=\frac{\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{W}f(x,y,z){\it {\,d} x}{\it {\,d} y}{\it {\,d} z}}{\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{W} {\it dx}\,{\it dy}\,{\it dz}}. \]
Again, notice that the denominator is chosen so that if \(f\) is a constant, say \(c\), then \([f]_{\rm av}=c\).
example 1
Find the average value of \(f(x,y)=x\sin^2(xy)\) on the region \(D=[0,\pi]\) \(\times\) \([0,\pi]\).
solution First, we compute \begin{eqnarray*} \intop\!\!\!\intop\nolimits_{D} f(x,y)\,{\it dx}\, {\it dy} &=& \int^\pi_0 \int^\pi_0 x\sin^2(xy)\,{\it dx}\,{\it dy}\\[4pt] &=&\int^\pi_0\left[ \int^\pi_0\frac{1-\cos(2xy)}{2}x\, {\it dy}\right]{\it {\,d} x}\\[4pt] &=&\int^\pi_0\left[\frac{y}{2}-\frac{\sin(2xy)} {4x}\right]x\bigg|^\pi_{y=0} {\it {\,d} x}\\[4pt] &=&\int^\pi_0\left[\frac{\pi x}{2}-\frac{\sin(2\pi x)}{4}\right]{\it dx}=\left[\frac{\pi x^2}{4}+ \frac{\cos(2\pi x)}{8\pi}\right]\bigg|^\pi_0\\[4pt] &=&\frac{\pi^3}{4}+\frac{\cos(2\pi^2)-1}{8\pi}.\\[-32pt] \end{eqnarray*}
330
Thus, the average value of \(f\), by formula (1), is \[ \frac{\pi^3/4+[\cos(2\pi^2)-1]/8\pi}{\pi^2}=\frac{\pi}{4}+\frac{\cos(2\pi^2)-1}{8\pi^3}\approx 0.7839. \]
example 2
The temperature at points in the cube \(W=[-1,1]\) \(\times\) \([-1,1]\) \(\times\) \([-1,1]\) is proportional to the square of the distance from the origin.
- (a) What is the average temperature?
- (b) At which points of the cube is the temperature equal to the average temperature?
solution (a) Let \(c\) be the constant of proportionality, so \(T=c(x^2+y^2+z^2)\) and the average temperature is \([T]_{\rm av}=\frac{1}{8}{\intop\!\!\intop\!\!\intop}_WT{\it dx}\,{\it dy}\,{\it dz}\), because the volume of the cube is 8. Thus, \[ [T]_{\rm av}=\frac{c}{8}\int^1_{-1}\int^1_{-1} \int^1_{-1}(x^2+y^2+z^2)\,{\it dx}\,{\it dy}\,{\it dz}. \]
The triple integral is the sum of the integrals of \(x^2,y^2\), and \(z^2\). Because \(x,y\), and \(z\) enter symmetrically into the description of the cube, the three integrals will be equal, so that \[ [T]_{\rm av}=\frac{3c}{8}\int^1_{-1}\int^1_{-1}\int^1_{-1}z^2{\it dx}\,{\it dy}\,{\it dz}=\frac{3c}{8} \int^1_{-1}z^2\left(\int^1_{-1}\int^1_{-1} {\it dx}\,{\it dy}\right)\,{\it dz}. \]
The inner integral is equal to the area of the square \([-1,1]\times[-1,1]\). The area of that square is 4, and so \[ [T]_{\rm av}=\frac{3c}{8}\int^1_{-1} 4z^2 {\it dz}=\frac{3c}{2}\left(\frac{z^3}{3}\right)\bigg|^1_{-1}=c. \]
(b) The temperature is equal to the average temperature at all points satisfying \(c(x^2+y^2+z^2)\,{=}\,c\)—that is, at all points lying on the sphere \(x^2+y^2+z^2\,{=}\,1\).

Question 16.66 Section 16.3 Progress Check Question #1
Find the average value of the function \(f(x,y) = x^2+y^2\) on the circular disk of radius two, centered at the origin.
Centers of Mass
If masses \(m_1,\ldots ,m_n\) are placed at points \(x_1,\ldots ,x_n\) on the \(x\) axis, their center of mass is defined to be \begin{equation*} \overline x=\frac{\sum m_ix_i}{\sum m_i}.\tag{2} \end{equation*}
This definition arises from the following observation: If one is balancing masses on a lever (Figure 16.15), the balance point \(\overline x\) occurs where the total moment (mass times distance from the balance point) is zero; that is, where \(\sum m_i(x_i-{\overline x})=0\). A physical principle, going back first to Archimedes and then in this generality to Newton, states that this condition means there is no tendency for the lever to rotate.
331
For a continuous mass density \(\delta (x)\) along the lever (measured in, say, grams/cm), the analogue of formula (2) is \begin{equation*} \overline x=\frac{\displaystyle\int x \delta (x)\,{\it dx}}{\displaystyle\int \delta(x)\,{\it dx}}.\tag{3} \end{equation*}
For two-dimensional plates, this generalizes to:
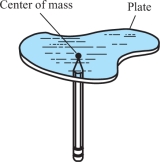
The Center of Mass of Two-Dimensional Plates
\begin{equation*} \overline x= \frac{\displaystyle\intop\!\!\!\intop\nolimits_{D} x\delta(x,y)\,{\it dx}\,{\it dy}}{\displaystyle\intop\!\!\!\intop\nolimits_{D} \delta(x,y)\,{\it dx}\, {\it dy}} \qquad \hbox{and}\qquad \skew2\overline y=\frac{\displaystyle\intop\!\!\!\intop\nolimits_{D} y\delta(x,y)\,{\it dx}\,{\it dy}}{\displaystyle\intop\!\!\!\intop\nolimits_{D} \delta(x,y)\,{\it dx}\, {\it dy}},\tag{4} \end{equation*} where again \(\delta(x,y)\) is the mass density (see Figure 16.16).
example 3
Find the center of mass of the rectangle \([0,1]\times[0,1]\) if the mass density is \(e^{x+y}\).
solution First we compute the total mass: \begin{eqnarray*} \intop\!\!\!\intop\nolimits_{D} e^{x+y}{\it dx}\,{\it dy} &=&\int^1_0\int^1_0 e^{x+y}{\it dx}\,{\it dy}=\int^1_0 \big(e^{x+y}\big|^1_{x=0}\big)\,{\it dy} =\int^1_0 (e^{1+y}-e^y)\, {\it dy}\\[6pt] &=& (e^{1+y}-e^y) \big|^1_{y=0}=e^2-e-(e-1)=e^2-2e+1. \end{eqnarray*}
The numerator in formula (4) for \(\overline x\) is \begin{eqnarray*} \int^1_0\!\!\int^1_0\!x e^{x+y}{\it dx}\,{\it dy} &=&\int^1_0\!(xe^{x+y}-e^{x+y})\big|^1_{x=0}{\it dy} =\int^1_0\![e^{1+y}-e^{1+y}-(0e^y-e^y)]\,{\it dy}\\[6pt] &=&\int^1_0e^y {\it dy}=e^y\Big|^1_{y=0}=e-1,\\[-15pt] \end{eqnarray*} so that \[ \overline x=\frac{e-1}{e^2-2e+1}=\frac{e-1}{(e-1)^2}=\frac{1}{e-1}\approx0.582. \]
The roles of \(x\) and \(y\) may be interchanged in all these calculations, so that \(\skew2\overline y=1/(e-1)\approx 0.582\) as well.
Question 16.67 Section 16.3 Progress Check Question #2
| Give the \(x\)- coordinate of the center of mass of the region bounded by \(y=4-x,x=0,y=0\) where \(\delta(x,y)=x\) | |
|---|---|
| Give the \(y\)- coordinate of the center of mass of the region bounded by \(y=4-x,x=0,y=0\) where \(\delta(x,y)=x\) |
For a region \(W\) in space with mass density \(\delta(x,y,z)\), we know that \begin{equation*} {\rm volume}= \intop\!\!\!\intop\!\!\!\intop\nolimits_{W}{\it dx}\,{\it dy}\,{\it dz},\tag{5} \end{equation*} \begin{equation*} {\rm mass}= \intop\!\!\!\intop\!\!\!\intop\nolimits_{W}\delta(x,y,z)\,{\it dx}\,{\it dy}\,{\it dz}.\tag{6} \end{equation*}
If we denote the coordinates of the center of mass by \((\overline x,\skew2\overline y,\skew2\overline z)\), then the generalization of the formulas in the preceding box are as follows.
332
Coordinates for the Center of Mass of Three-Dimensional Regions
\begin{equation*} \displaystyle \overline x=\frac{\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{\! W}x\delta (x,y,z)\,{\it dx}\,{\it dy}\,{\it dz}}{{\rm mass}}\\[6pt] \displaystyle \skew2\overline y=\frac{\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{\! W}y\delta (x,y,z)\,{\it dx}\,{\it dy}\,{\it dz}}{{\rm mass}}\\[6pt] \displaystyle \skew2\overline z=\frac{\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{\! W}z\delta (x,y,z)\,{\it dx}\,{\it dy}\,{\it dz}}{{\rm mass}}\tag{7} \end{equation*}
example 4
The cube \([1,2]\times [1,2]\times [1,2]\) has mass density given by \(\delta(x,y,z)=(1+x)e^zy\). Find the total mass of the box.
solution The mass of the box is, by formula (6), \begin{eqnarray*} &&\int^2_1\int^2_1\int^2_1(1+x)e^zy\,{\it dx}\,{\it dy}\,{\it dz} =\int^2_1\int^2_1\left[\left(x+\frac{x^2}{2}\right)e^zy\right]^{x=2}_{x=1}{\it dy}\,{\it dz}\\[5pt] &&\quad =\int^2_1\int^2_1 \frac{5}{2}e^zy\,{\it dy}\,{\it dz} =\int^2_1\frac{15}{4}e^z{\it dz}=\left[\frac{15}{4}e^z\right]^{z=2}_{z=1} = \frac{15}{4}(e^2-e).\\[-36pt] \end{eqnarray*}
If a region and its mass density are reflection-symmetric across a plane, then the center of mass lies on that plane. For example, in formula (7) for \(\overline x\), if the region and mass density are symmetric in the \(yz\) plane, then the integrand is odd in \(x\), and so \(\overline x=0\). This kind of use of symmetry is illustrated in the next example.
example 5
Find the center of mass of the hemispherical region \(W\) defined by the inequalities \(x^2+y^2+z^2\leq 1,z \geq 0\). (Assume that the density is unity.)
solution By symmetry, the center of mass must lie on the \(z\) axis, and so \(\overline x=\skew2\overline y=0\). To find \(\skew2\overline z\), we must compute, by formula (7), the numerator \(I={\intop\!\!\intop\!\!\intop}_W z\,{\it dx}\,{\it dy}\,{\it dz}\). The hemisphere is an elementary region, and thus the integral becomes \[ I=\int^1_0\int^{\sqrt{1-z^2}}_{-\sqrt{1-z^2}} \int^{\sqrt{1-y^2-z^2}}_{-\sqrt{1-y^2-z^2}}z\, {\it dx}\,{\it dy}\,{\it dz}. \]
Because \(z\) is a constant for the \(x\) and \(y\) integrations, we can remove it from the first two integral signs, to obtain \[ I=\int^1_0 z\left(\int^{\sqrt{1-z^2}}_{-\sqrt{1-z^2}} \int^{\sqrt{1-y^2-z^2}}_{-\sqrt{1-y^2-z^2}}{\it dx}\,{\it dy}\right)dz. \]
Instead of calculating the inner two integrals explicitly, we observe that they equal the double integral \({\intop\!\!\intop}_D {\it dx}\,{\it dy}\) over the disk \(x^2+y^2\leq 1-z^2\), considered as an \(x\)-simple region in the plane. The area of this disk is \(\pi(1-z^2)\), and so \[ I=\pi\int^1_0 z(1-z^2)\,{\it dz}=\pi\int^1_0(z-z^3)\,{\it dz}=\pi\left[\frac{z^2}{2}- \frac{z^4}{4}\right]^1_0=\frac{\pi}{4}. \]
333
The volume of the hemisphere is \(\frac{2}{3}\pi\), and so \(\skew2\overline z=(\pi/4)/( \frac{2}{3}\pi)=\frac{3}{8}\).

Historical Note
It is common knowledge that Archimedes observed the principle of the lever. Perhaps less known is that he was also responsible for discovering the concepts of center of mass and center of gravity. Only two of his works on mechanics have been handed down to us: On Floating Bodies and On the Equilibrium and Centers of Mass of Plane Figures. Both were translated into Latin by Niccolo Tartaglia, circa 1543.
In Equilibrium\(\ldots\), Archimedes began the field of applied mathematics, doing for mechanics what Euclid had accomplished for geometry. In this work he describes the principles behind all the machines of antiquity, including the lever, inclined plane, and pulley systems.
Surprisingly, Archimedes never carefully defined the center of mass; the first proper definition was given by Pappus of Alexandria in 340 C.E. The concept of equilibrium was to have a profound effect on the development of mechanical engineering (through the introduction of gears), architecture, and in art, permitting the construction of complex machines, large-scale buildings, and sculptures. Figure 16.17 shows sketches by Leonardo DaVinci, illustrating equilibrium positions of the human body.
Moments of Inertia
Another important concept in mechanics, one that is needed in studying the dynamics of a rotating rigid body, is that of moment of inertia. If the solid \(W\) has uniform density \(\delta\), the moments of inertia \(I_x,I_y\), and \(I_z\) about the \(x,y\), and \(z\) axes, respectively, are defined by:
334
Moments of Inertia About the Coordinate Axes
\begin{equation*} \begin{array}{c} I_x=\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{W} (y^2+z^2)\,\delta\,dx{\it dy}\,{\it dz}, I_y=\intop\!\!\!\intop\!\!\!\intop\nolimits_{W} (x^2+z^2)\,\delta\,{\it dx}\,{\it dy}\,{\it dz},\\[9pt] I_z=\displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{W} (x^2+y^2)\, \delta\,{\it dx}\,{\it dy}\,{\it dz}. \end{array}\tag{8} \end{equation*}
The moment of inertia measures a body’s response to efforts to rotate it; for example, as when one tries to rotate a merry-go-round. The moment of inertia is analogous to the mass of a body, which measures its response to efforts to translate it. In contrast to translational motion, however, the moments of inertia depend on the shape and not just the total mass. It is harder to spin up a large plate than a compact ball of the same mass.
For example, \(I_x\) measures the body’s response to forces attempting to rotate it about the \(x\) axis. The factor \(y^2 + z^2\), which is the square of the distance to the \(x\) axis, weights masses farther away from the rotation axis more heavily. This is in agreement with the intuition just explained.
example 6
Compute the moment of inertia \(I_z\) for the solid above the \(xy\) plane bounded by the paraboloid \(z=x^2+y^2\) and the cylinder \(x^2+y^2=a^2\), assuming \(a\) and the mass density to be constants.
solution The paraboloid and cylinder intersect at the plane \(z=a^2\). Using cylindrical coordinates, we find from equation (8), \[ I_z=\int^a_0\int^{2\pi}_0 \int^{r^2}_0\delta r^2\ {\cdot}\ r{\it dz}{\,d} \theta {\,d} r=\delta \int^a_0 \int^{2\pi}_0\int^{r^2}_0 r^3{\it dz}\,{\,d} \theta {\,d} r=\frac{\pi \delta a^6}{3}. \]
Question 16.68 Section 16.3 Progress Check Question #3
Let \(W = \{(x,y,z) \in \mathbb{R}^3 \ | \ 0 \leq x^2+y^2 \leq R^2, -R \leq z \leq R \}\). Find \(I_z\). the moment of inertia of \(W\) about the \(z\)-axis, assuming \(R\) and the mass density \(\delta\) to be positive constants.
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
Gravitational Fields of Solid Objects
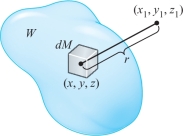
Another interesting physical application of triple integration is the determination of the gravitational fields of solid objects. Example 7, Section 2.6, showed that the gravitational force field \({\bf F}(x,y,z)\) of a particle is the negative of the gradient of a function \(V(x,y,z)\) called the gravitational potential. If there is a point mass \(M\) at \((x,y,z)\), then the gravitational potential acting on a mass \(m\) at \((x_1,y_1,z_1)\) due to this mass is \(-GmM[(x-x_1)^2+(y-y_1)^2+(z-z_1)^2]^{-1/2}\), where \(G\) is the universal gravitational constant.
If our attracting object occupies a domain \(W\) with mass density \(\delta(x,y,z)\), we may think of it as made of infinitesimal box-shaped regions with masses \(dM=\delta(x,y,z)\,{\it dx}\,{\it dy}\,{\it dz}\) located at points \((x,y,z)\). The total gravitational potential \(V\) for \(W\) is then obtained by “summing” the potentials from the infinitesimal masses. Thus, we arrive at the triple integral (see Figure 16.18): \begin{equation*} V(x_1,y_1,z_1)= -{\it Gm}\intop\!\!\!\intop\!\!\!\intop\nolimits_{W}\frac{\delta(x,y,z)\,{\it dx}\,{\it dy}\,{\it dz}}{\sqrt{(x-x_1)^2+( y-y_1)^2 + (z-z_1)^2}}.\tag{9} \end{equation*}
335
Historical Note
The theory of gravitational force fields and gravitational potentials was developed by Sir Isaac Newton (1642–1727). Newton withheld publication of his gravitational theories for quite some time. The result that a spherical planet has the same gravitational field as it would have if its mass were all concentrated at the planet’s center first appeared in his famous Philosophiae Naturalis Principia Mathematica, the first edition of which appeared in 1687. Using multiple integrals and spherical coordinates, we shall solve Newton’s problem here; remarkably, Newton’s published solution used only Euclidean geometry.
example 7
Let \(W\) be a region of constant density and total mass \(M\). Show that the gravitational potential is given by \[ V(x_1,y_1,z_1)=\left[\frac{1}{r}\right]_{\rm av} {\it GMm}, \] where \([1/r]_{\rm av}\) is the average over \(W\) of \[ f(x,y,z)=\frac{1}{\sqrt{(x-x_1)^2+( y-y_1)^2+(z-z_1)^2}}. \]
solution According to formula (9), \begin{eqnarray*} -V(x_1,y_1,z_1) & = & {\it Gm}\intop\!\!\!\intop\!\!\!\intop\nolimits_{W}\frac{\delta\, {\it dx}\,{\it dy}\,{\it dz}}{\sqrt{(x-x_1)^2+(y-y_1)^2+(z-z_1)^2}}\\ [10pt] & = & {\it Gm}\delta\intop\!\!\!\intop\!\!\!\intop\nolimits_{W}\frac{{\it dx}\,{\it dy}\,{\it dz}}{\sqrt{(x-x_1)^2+(y-y_1)^2+(z-z_1)^2}}\\[10pt] & = & {\it Gm}[\delta \hbox{ volume } (W)]\frac{ \displaystyle\intop\!\!\!\intop\!\!\!\intop\nolimits_{W} \displaystyle \frac{ {\it dx}\,{\it dy}\,{\it dz}}{\sqrt{(x-x_1)^2+(y-y_1)^2+(z-z_1)^2}}}{{\rm volume}\, (W)}\\ &=&{\it GmM}\left[\frac{1}{r}\right]_{\rm av} \end{eqnarray*} are required.
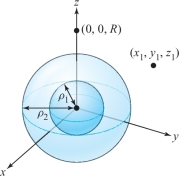
Let us now use formula (9) and spherical coordinates to find the gravitational potential \(V(x_1,y_1,z_1)\) for a region \(W\) with constant density between the concentric spheres \(\rho=\rho_1\) and \(\rho=\rho_2\), assuming the density is constant. Before evaluating the integral in formula (9), we make some observations that will simplify the computation. Because \(G,m,\) and the density are constants, we may ignore them at first. Because the attracting body, \(W\), is symmetric with respect to rotations about the origin, the potential \(V(x_1,y_1,z_1)\) should itself be symmetric—thus, \(V(x_1,y_1,z_1)\) depends only on the distance \(R={\sqrt{x_1^2+y_1^2+z^2_1}}\) from the origin. Our computation will be simplest if we look at the point \((0,0,R)\) on the \(z\) axis (see Figure 16.19). Thus, we need to evaluate the integral \[ V(0,0,R)=-\!\!\intop\!\!\!\intop\!\!\!\intop\nolimits_{W} \frac{{\it dx}\,{\it dy}\,{\it dz}}{\sqrt{x^2+y^2+(z-R)^2}}. \]
336
In spherical coordinates, \(W\) is described by the inequalities \(\rho_1\leq \rho\leq \rho_2,0\leq \theta \leq 2\pi\), and \(0\leq \phi \leq \pi\), and so \[ -V(0,0,R)=\int^{\rho_{2}}_{\rho_1}\int^\pi_0\int^{2\pi}_0 \frac{\rho^2\sin \phi {\,d} \theta {\,d} \phi {\,d} \rho} {\sqrt{\rho^2\sin^2\phi(\cos^2\theta +\sin^2\theta)+(\rho \cos \phi-R)^2}}. \]
Replacing \(\cos^2\theta\) \(+\) \(\sin^2\theta\) by 1, so that the integrand no longer involves \(\theta\), we may integrate over \(\theta\) to get \begin{eqnarray*} -V(0,0,R) &=& 2\pi\int^{\rho_{2}}_{\rho_1}\int^\pi_0 \frac{\rho^2\sin\phi {\,d} \phi {\,d} \rho}{\sqrt{\rho^2\sin^2\phi +(\rho \cos \phi-R)^2}}\\[5pt] &=& 2\pi\int^{\rho_{ 2}}_{\rho_1}\rho^2\left(\int^{\pi}_0 \frac{\sin\phi {\,d} \phi}{\sqrt{\rho^2-2R\rho\cos \phi+R^2}}\right)d\rho. \end{eqnarray*}
The inner integral over \(\phi\) may be evaluated using the substitution \(u= - 2R\rho \cos\phi\). We get \begin{eqnarray*} \frac{1}{2R\rho}\int^{2R \rho}_{-2R\rho}(\rho^2+u+R^2)^{-1/2}{\,d} u &=&\frac{2}{2R\rho}(\rho^2+u+R^2)^{1/2}\bigg|^{2R\rho}_{-2R\rho}\\[5pt] &=&\frac{1}{R\rho}\big[(\rho^2\,{+}\,2R\rho\,{+}\,R^2)^{1/2}\,{-}\,(\rho^2-2R\rho\,{+}\,R^2)^{1/2}\big]\\[5pt] &=&\frac{1}{R\rho}\big\{[(\rho+R)^2]^{1/2}-[(\rho-R)^2]^{1/2}\big\}\\[5pt] &=& \frac{1}{R\rho}(\rho+R-|\rho-R|). \end{eqnarray*}
The expression \(\rho +R\) is always positive, but \(\rho-R\) may not be, so we must keep the absolute value sign. Substituting into the formula for \(V\), we get \[ -V(0,0,R) = 2\pi\!\int^{\rho_{ 2}}_{\rho_1}\!\!\frac{\rho^2}{R\rho}(\rho+R-|\rho-R|)\, d\rho = \frac{2\pi}{R}\!\int^{\rho_{ 2}}_{\rho_1}\!\!\rho(\rho+R-|\rho-R|)\, d\rho. \]
We consider two possibilities for \(R\), corresponding to the gravitational potential for objects outside and inside the hollow ball \(W\).
Case 1. If \(R\geq \rho_2\) [that is, if \((x_1,y_1,z_1\)) is outside \(W\)], then \(|\rho-R|=R-\rho\) for all \(\rho\) in the interval \([\rho_1,\rho_2]\), so that \begin{eqnarray*} -V(0,0,R) = \frac{2\pi}{R}\int^{\rho_{ 2}}_{\rho_1}\rho[\rho+R-(R-\rho)]{\,d} \rho = \frac{4\pi}{R}\int^{\rho_{ 2}}_{\rho_1}\rho^2\, d\rho =\frac{1}{R} \frac{4\pi}{3} \big(\rho^3_2-\rho^3_1\big). \end{eqnarray*}
The factor \((4\pi/3)(\rho^3_2-\rho^3_1)\) equals the volume of \(W\). Putting back the constants \(G, m\), and the mass density, we find that the gravitational potential is \(-GmM/R\), where \(M\) is the mass of \(W\). Thus, \(V\) is just as it would be if all the mass of \(W\) were concentrated at the central point.
337
Case 2. If \(R\leq \rho_1\) [that is, if \((x_1,y_1,z_1)\) is inside the hole], then \(|\rho-R|=\rho-R\) for \(\rho\) in \([\rho_1,\rho_2]\), and so \begin{eqnarray*} -V(0,0,R)&=&({\it Gm})\frac{2\pi}{R}\int^{\rho_{ 2}}_{\rho_1}\rho[\rho + R-(\rho-R)]{\,d} \rho= ({\it Gm})4\pi\int^{\rho_{ 2}}_{\rho_1}\rho {\,d} \rho\\ &=& ({\it Gm})2\pi \big(\rho^2_2-\rho^2_1 \big). \end{eqnarray*}
The result is independent of \(R\), and so the potential \(V\) is constant inside the hole. Because the gravitational force is minus the gradient of \(V\), we conclude that there is no gravitational force inside a uniform hollow planet!
We leave it to you to compute \(V(0,0,R)\) for the case \(\rho_1<R<\rho_2\).
A similar argument shows that the gravitational potential outside any spherically symmetric body of mass \(M\) (even if the density is variable) is \(V=GMm/R\), where \(R\) is the distance to its center (which is its center of mass).
example 8
Find the gravitational potential acting on a unit mass of a spherical star with a mass \(M=3.02\times 10^{30}\) kg at a distance of \(2.25 \times 10^{11}\) m from its center \((G=6.67\times 10^{-11}\) N\(\,{\cdot}\,\)m\(^2\hbox{/}\)kg\(^2)\).
solution The negative potential is \[ -V=\frac{\it GM}{R}=\frac{6.67\times 10^{-11}\times 3.02\times 10^{30}} {2.25\times 10^{11}}=8.95\times 10^8\ \ {\rm m^2\hbox{/}s^2}. \]