17.5 Integrals of Scalar Functions Over Surfaces
393
Now we are ready to define the integral of a scalar function \(f\) over a surface \(S\). This concept is a natural generalization of the area of a surface, which corresponds to the integral over \(S\) of the scalar function \(f(x, y, z) = 1\). This is quite analogous to considering the path integral as a generalization of arc length. In the next section we shall deal with the integral of a vector function \({\bf F}\) over a surface. These concepts will play a crucial role in the vector analysis treated in the final chapter.
Let us start with a surface \(S\) parametrized by a mapping \({\Phi}\colon\, D\to S \subset {\mathbb R}^3\), where D is an elementary region, which we write as \({\Phi}(u,v) = (x(u,v),y(u,v), z(u,v))\).
Definition: The Integral of a Scalar Function Over a Surface
If \(f(x, y, z)\) is a real-valued continuous function defined on a parametrized surface \(S\), we define the integral of f over \(S\) to be \begin{equation*} \int\!\!\!\int\nolimits_{S}f(x,y,z) \,dS = \int\!\!\!\int\nolimits_{S} f \,dS = \int\!\!\!\int\nolimits_{D} f({\Phi}(u,v)) \|{\bf T}_u \times {\bf T}_v\| \,du \,dv.\tag{1} \end{equation*}
Written out, equation (1) becomes \begin{equation*} \begin{array}{lll} \int\!\!\!\int\nolimits_{S}f\,dS &=& \int\!\!\!\int\nolimits_{D}f(x(u,v),y(u,v),z(u,v)) \,\sqrt{\bigg[\frac{\partial(x,y)}{\partial(u,v)}\bigg]^2 +\bigg[\frac{\partial(y,z)}{\partial(u,v)}\bigg]^2 + \bigg[\frac{\partial(x,z)}{\partial(u,v)}\bigg]^2} d u \,dv. \end{array}\tag{2} \end{equation*}
Thus, if \(f\) is identically 1, we recover the area formula (3) of Section 17.4. Like surface area, the surface integral is independent of the particular parametrization used. This will be discussed in Section 17.6.
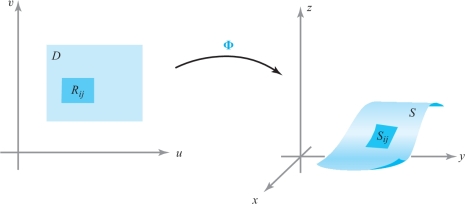
We can gain some intuitive knowledge about this integral by considering it as a limit of sums. Let \(D\) be a rectangle partitioned into \(n^2\) rectangles \(R_{\it ij}\) with areas \(\Delta u\, \Delta v\). Let \(S_{\it ij}={\Phi}(R_{\it ij})\) be the portion of the surface \({\Phi}(D)\) corresponding to \(R_{\it ij}\) (see Figure 17.38), and let \(A(S_{\it ij})\) be the area of this portion of the surface. For large \(n, f\) will be approximately constant on \(S_{\it ij}\), and we form the sum \begin{equation*} S_n = \sum_{i=0}^{n-1} \sum_{j=0}^{n-1} f({\Phi}(u_i,v_j))A(S_{\it ij}),\tag{3} \end{equation*} where \((u_i,v_j)\in R_{\it ij}\). From Section 17.4 we have a formula for \(A(S_{\it ij}) \): \[ A(S_{\it ij}) = \int\!\!\!\int\nolimits_{R_{\it ij}} \|{\bf T}_u \times {\bf T}_v\| \,du \,dv, \] which, by the mean-value theorem for integrals, equals \(\|{\bf T}_{u_i^*} \times {\bf T}_{v_j^*}\|\, { \Delta} u \,{ \Delta} v\) for some point \((u_i^*,v_j^*)\) in \(R_{\it ij}\). Hence, our sum becomes \[ S_n = \sum_{i=0}^{n-1} \sum_{j=0}^{n-1} f({\Phi}(u_i,v_j)) \|{\bf T}_{u_i^*} \times {\bf T}_{v_j^*}\| { \Delta} u\, { \Delta} v, \] which is an approximating sum for the last integral in formula (1). Therefore, \[ {\mathop {\rm limit}_{n\to \infty}\ } S_n = \int\!\!\!\int\nolimits_{S} f \,dS. \]
394
Note that each term in the sum in formula (3) is the value of \(f\) at some point \({\Phi}(u_i,v_j)\) times the area of \(S_{\it ij}\). Compare this with the Riemann-sum interpretation of the path integral in Section 17.1.
If \(S\) is a union of parametrized surfaces \(S_i,\ i=1,\ldots,N\), that do not intersect except possibly along curves defining their boundaries, then the integral of \(f\) over \(S\) is defined by \[ \int\!\!\!\int\nolimits_{S} f\,dS = \sum_{i=1}^N \int\!\!\!\int\nolimits_{S_i} f \,dS, \] as we should expect. For example, the integral over the surface of a cube may be expressed as the sum of the integrals over the six sides.
example 1
Suppose a helicoid is described as in Example 2, Section 17.4, and let \(f\) be given by \(f(x,y,z) = \sqrt{x^2+y^2 +1}\). Find \({\int\!\!\!\int}_S f \,dS\).
solution As in Examples 1 and 2 of Section 17.4, \[ \frac{\partial(x,y)}{\partial(r,\theta)} = r, \qquad \frac{\partial(y,z)}{\partial(r,\theta)} =\sin \theta,\qquad \frac{\partial(x,z)}{\partial(r,\theta)} = \cos\theta. \]
Also, \(f(r\cos\theta,r\sin\theta,\theta) = \sqrt{r^2 + 1}\). Therefore, \begin{eqnarray*} \int\!\!\!\int\nolimits_{S}f(x,y,z) \,dS &=& \int\!\!\!\int\nolimits_{D} f({\Phi}(r,\theta))\|{\bf T}_r \times {\bf T}_{\theta}\| \,dr \,d\theta\\[5pt] &=& \int_0^{2\pi} \int_0^1 \sqrt{r^2 + 1} \sqrt{r^2 + 1} \,dr \,d\theta = \int_0^{2\pi} \frac{4}{3} \,d\theta = \frac{8}{3} \pi.\\[-28pt] \end{eqnarray*}
Question 17.114 Section 17.5 Progress Check Question #1
Let the surface \(S\) be parameterized by \({\bf \Phi} (u,v) = (u \cos (v), u \sin (v), u)\) where \(0 \leq u,v \leq 1\). Find \(\displaystyle{\int\!\!\!\int}_S \ z(x^2+y^2) \,dS\).
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
Surface Integrals Over Graphs
Suppose \(S\) is the graph of a \(C^1\) function \(z=g(x,y)\). Recall from Section 17.4 that we can parametrize \(S\) by \[ x=u,\qquad y = v,\qquad z = g(u,v), \] and that in this case \[ \|{\bf T}_u \times {\bf T}_v\| = \sqrt{1+\bigg(\frac{\partial g}{\partial u}\bigg)^2 + \bigg(\frac{\partial g}{\partial v}\bigg)^2}, \] so \begin{equation*} \int\!\!\!\int\nolimits_{S} f(x,y,z) \,dS = \int\!\!\!\int\nolimits_{D} f(x,y,g(x,y)) \sqrt{1+\bigg(\frac{\partial g}{\partial x}\bigg)^2+ \bigg(\frac{\partial g}{\partial y}\bigg)^2} \,{\it dx} \,{\it dy}.\tag{4} \end{equation*}
395
example 2
Let \(S\) be the surface defined by \(z = x^2 + y\), where \(D\) is the region \(0 \le x \le 1, -1 \le y \le 1\). Evaluate \({\int\!\!\!\int}_S x \,dS\).
solution If we let \(z = g(x,y) = x^2 + y\), formula (4) gives \begin{eqnarray*} \int\!\!\!\int\nolimits_{S} x \,dS &=& \int\!\!\!\int\nolimits_{D} x \sqrt{1+\bigg(\frac{\partial g}{\partial x}\bigg)^2 + \bigg(\frac{\partial g}{\partial y}\bigg)^2} \,{\it dx} \,{\it dy} = \int_{-1}^1 \int_0^1 x \sqrt{1 + 4x^2 + 1} \,{\it dx} \,{\it dy} \\[5pt] &=& \frac{1}{8} \int_{-1}^1 \bigg[\int_0^1 (2+4x^2)^{1/2} (8x\,{\it dx} )\bigg] {\it dy} = \frac23 \,\, {\cdot}\, \, \frac18 \int_{-1}^1 [(2 + 4x^2)^{3/2}]|^1_0 \,{\it dy} \\[5pt] & = & \frac{1}{12} \int_{-1}^1 (6^{3/2} - 2^{3/2}) \,{\it dy} = \frac{1}{6}(6^{3/2}- 2^{3/2}) = \sqrt{6} - \frac{\sqrt{2}}{3}\\ [5pt] & = & \sqrt{2} \bigg(\sqrt{3} - \frac{1}{3}\bigg).\\[-28pt] \end{eqnarray*}
Question 17.115 Section 17.5 Progress Check Question #2
Let the surface \(S\) be given by \(\displaystyle z=4-x^2\) where \(0 \leq x,y \leq 2\) and let \(\displaystyle f(x,y,z)= x\). Find \(\displaystyle{\int\!\!\!\int}_S \ f \,dS\).
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
example 3
Evaluate \(\int\!\!\!\int\nolimits_{\! S} z^2 \,dS\), where \(S\) is the unit sphere \(x^2 + y^2 + z^2 =1\).
solution For this problem, it is convenient to use spherical coordinates and to represent the sphere parametrically by the equations \(x = \cos\theta\sin\phi,y=\sin\theta\sin\phi,z=\cos\phi\), over the region \(D\) in the \(\theta\phi\) plane given by the inequalities \(0\le \phi \le \pi, 0\le \theta \le 2\pi\). From equation (1) we get \[ \int\!\!\!\int\nolimits_{S} z^2 \,dS = \int\!\!\!\int\nolimits_{D} (\cos \phi)^2 \|{\bf T}_{\theta}\times {\bf T}_{\phi}\| \,d\theta \,d\phi. \]
A little computation [use formula (2) of Section 17.4; see Exercise 12] shows that \[ \|{\bf T}_{\theta}\times {\bf T}_{\phi}\| = \sin \phi . \] (Note that for \(0\leq\phi\leq \pi, \hbox{ we have } \sin \phi\geq 0.)\) Thus, \begin{eqnarray*} \int\!\!\!\int\nolimits_{S} z^2 \,dS &=& \int_0^{2\pi} \int_0^{\pi} \cos^2 \phi \sin\phi \,d\phi \,d\theta \\[4pt] & = & \frac{1}{3} \int_0^{2\pi} [-{\rm cos}^3 \phi]_0^{\pi} \,d\theta = \frac{2}{3} \int_0^{2\pi} \,d\theta = \frac{4\pi}{3}.\\[-28pt] \end{eqnarray*}
This example also shows that on a sphere of radius R, \[ \int\!\!\!\int_{S} f \ {\it ds} = \int_{0}^{2\pi} \int_{0}^{\pi} f(\phi,\theta) {\it R}^2 \sin \phi \, d\phi \, d\theta, \] or, for short, the area element on the sphere is given by \[ dS = {\it R}^2 \sin\phi \, d\phi \, d\theta. \]
Question 17.116 Section 17.3 Progress Check Question #3
Evaluate \(\displaystyle \int\!\!\!\int\nolimits_{\! S} x \,dS\), where \(S\) is the unit sphere \(\displaystyle x^2 + y^2 + z^2 =1\).
| A. |
| B. |
| C. |
| D. |
| E. |
Integrals Over Graphs
396
We now develop another formula for surface integrals when the surface can be represented as a graph. To do so, we let \(S\) be the graph of \(z =g(x, y)\) and consider formula (4). We claim that \begin{equation*} \int\!\!\!\int\nolimits_{S} f(x,y,z) \,dS = \int\!\!\!\int\nolimits_{D}\frac{f(x,y,g(x,y))}{\cos\theta}\,{\it dx} \,{\it dy},\tag{5} \end{equation*} where \(\theta\) is the angle the normal to the surface makes with the unit vector \({\bf k}\) at the point \((x, y, g(x, y))\) (see Figure 17.39). Describing the surface by the equation \(\phi(x,y,z) = z-g(x,y) = 0\), a normal vector \({\bf N}\) is \(\nabla\phi\); that is, \begin{equation*} {\bf N} = -\frac{\partial g}{\partial x}{\bf i} - \frac{\partial g}{\partial y}{\bf j} + {\bf k}\tag{6} \end{equation*}
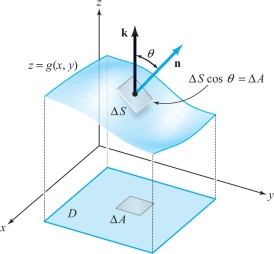
[see Example 4 of Section 17.3, or recall that the normal to a surface with equation \(g(x, y, z) = \hbox{constant is given by } \nabla g\)]. Thus, \[ \cos\theta = \frac{{\bf N}\, {\cdot}\, {\bf k}}{\|{\bf N}\|} = \frac{1}{\sqrt{(\partial g/\partial x)^2+(\partial g/\partial y)^2 +1}} . \]
Substitution of this formula into equation (4) gives equation (5). Note that \({\cos\theta={\bf n} \,{\cdot}\, {\bf k}}\), where \({{\bf n}={\bf N}/\|{\bf N}\|}\) is the unit normal. Thus, we can write \[ d{\bf S}= \frac{{\it dx}\ {\it dy}}{{\bf n}\, {\cdot}\,{\bf k}}. \]
The result is, in fact, obvious geometrically, for if a small rectangle in the \({\it xy}\) plane has area \({\Delta} A\), then the area of the portion above it on the surface is \({\Delta} S = { \Delta} A{/}\cos\theta\) (Figure 17.39). This intuitive approach can help us to remember formula (5) and to apply it in problems.
397
example 4
Compute \({\int\!\!\!\int}_S x \,dS\), where \(S\) is the triangle with vertices \((1,0,0), (0, 1,0), (0, 0, 1)\) (see Figure 17.40).
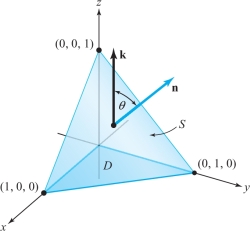
solution This surface is the plane described by the equation \(x + y + z = 1\). Because the surface is a plane, the angle \(\theta\) is constant and a unit normal vector is \({\bf n} = (1/\sqrt{3},1/\sqrt{3},1/\sqrt{3})\). Thus, \(\cos\theta ={\bf n}{\, {\cdot}\, }{\bf k} = 1/\sqrt{3}\), and by equation (5), \[ \int\!\!\!\int\nolimits_{S} x \,dS = \sqrt{3}\int\!\!\!\int\nolimits_{D} x \,{\it dx} \,{\it dy} , \] where \(D\) is the domain in the \({\it xy}\) plane. But \[ \sqrt{3}\int\!\!\!\int\nolimits_{D} x\,{\it dx} \,{\it dy} = \sqrt{3} \int_0^1 \int_0^{1-x} x \,{\it dy}\,{\it dx} = \sqrt{3}\int_0^1 x(1-x)\,{\it dx} = \frac{\sqrt{3}}{6}. \]
Integrals of functions over surfaces are useful for computing the mass of a surface when the mass density function \(m\) is known. The total mass of a surface with mass density (per unit area) \(m\) is given by \begin{equation*} M(S\,) = \int\!\!\!\int\nolimits_{S} m(x,y,z)\,dS.\tag{7} \end{equation*}
example 5
Let \({\Phi}\colon\, D \to {\mathbb R}^3\) be the parametrization of the helicoid \(S = {\Phi}(D)\) of Example 2 of Section 17.4. Recall that \({\Phi}(r,\theta) = (r\cos\theta, r \sin\theta,\theta)\), where \(0 \le \theta \le 2\pi\), and \(0 \le r \le 1\). Suppose \(S\) has a mass density at \((x, y, z)\in S\) equal to twice the distance of \((x, y, z)\) from the central axis (see Figure 17.31), that is, \(m(x, y, z)=2\sqrt{x^2 + y^2} = 2r\), in the cylindrical coordinate system. Find the total mass of the surface.
solution Applying formula (7), \[ M(S\,) = \int\!\!\!\int\nolimits_{S} 2 \sqrt{x^2 + y^2}\,d S = \int\!\!\!\int\nolimits_{D} 2r \,dS = \int\!\!\!\int\nolimits_{D} 2r\|{\bf T}_r \times {\bf T}_{\theta}\| \,dr \,d\theta. \]
From Example 2 of Section 17.4, we see that \(\|{\bf T}_r \times {\bf T}_{\theta}\| = \sqrt{1 + r^2}\). Thus, \begin{eqnarray*} M(S\,) &=& \int\!\!\!\int\nolimits_{D} 2r \sqrt{1 + r^2} \,dr \,d\theta = \int_0^{2\pi}\int_0^1 2r\sqrt{1+r^2} \,dr \,d\theta\\[5pt] &=& \int_0^{2\pi} \left[ \frac23 (1+r^2)^{3/2}\right]_0^1 \,d\theta = \int_0^{2\pi} \frac23 \, (2^{3/2} - 1) \,d\theta = \frac{4\pi}{3} (2^{3/2} - 1).\\[-28pt] \end{eqnarray*}