17.6 Surface Integrals of Vector Fields
The goal of this section is to develop the notion of the integral of a vector field over a surface. Recall that the definition of the line integral of a vector field was motivated by the fundamental physical notion of work. Similarly, there is a basic physical notion of flux that motivates the definition of the surface integral of a vector field.
For example, if the vector field is the velocity field of a fluid (perhaps the velocity field of a flowing river), and we put an imagined mathematical surface into the fluid, we can ask: “What is the rate at which fluid is crossing the given surface (measured in, say, cubic meters per second)?” The answer is given by the surface integral of the fluid velocity vector field over the surface.
We shall come back to the physical interpretation shortly and reconcile it with the formal definition that we give first.
Definition of the Surface Integral
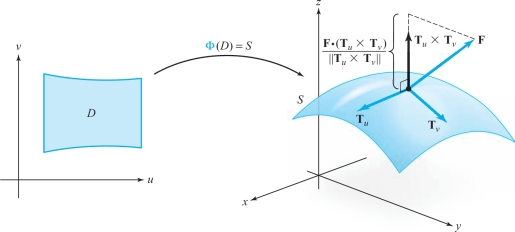
We now define the integral of a vector field, denoted \({\bf F}\), over a surface \(S\). We first give the definition and later in this section give its physical interpretation. This can also be used as a motivation for the definition if you so desire. Also, we shall start with a parametrized surface \({\Phi}\) and later study the question of independence of parametrization.
Definition: The Surface Integral of Vector Fields
Let \({\bf F}\) be a vector field defined on \(S\), the image of a parametrized surface \({\Phi}\). The surface integral of \({\bf F}\) over \({\Phi}\), denoted by \[ \int\!\!\!\int\nolimits_{\Phi} {\bf F}\,{\cdot}\,d{\bf S}, \] is defined by (see Figure 17.41) \[ \int\!\!\!\int\nolimits_{\Phi}{\bf F}\, {\cdot} \,d{\bf S} =\int\!\!\!\int\nolimits_{D}{\bf F}\, {\cdot}\, ({\bf T}_u\times {\bf T}_v) \,du \,dv. \]
401
example 1
Let \(D\) be the rectangle in the \(\theta\phi\) plane defined by \[ 0\leq \theta \leq 2\pi,\qquad 0\leq \phi \leq \pi, \] and let the surface \(S\) be defined by the parametrization \({\Phi}\colon\, D\to {\mathbb R}^3\) given by \[ x=\cos\theta \sin\phi,\qquad y=\sin\theta\sin\phi,\qquad z=\cos\phi. \]
(Thus, \(\theta\) and \(\phi\) are the angles of spherical coordinates, and \(S\) is the unit sphere para- metrized by \({\Phi}\).) Let \({\bf r}\) be the position vector \({\bf r}(x,y,z)=x{\bf i}+y{\bf j}+z{\bf k}\). Compute \(\int\!\!\!\int\nolimits_{\Phi} {\bf r}\,{\cdot}\,d{\bf S}\).
solution First we find \begin{eqnarray*} && {\bf T}_{\theta}=({-}\!\sin\phi\sin\theta){\bf i}+(\sin\phi\cos\theta){\bf j}\\ && {\bf T}_{\phi}=(\cos\theta\cos\phi){\bf i}+(\sin\theta\cos\phi){\bf j}-(\sin\phi){\bf k},\\[-23.7pt] \end{eqnarray*} and hence \[ {\bf T}_{\theta}\times {\bf T}_{\phi}=(-{\rm sin}^2\phi\cos\theta){\bf i}-(\sin^2\phi\sin\theta){\bf j} -(\sin\phi\cos\phi){\bf k}. \]
Then we evaluate \begin{eqnarray*} {\bf r}\, {\cdot}\, ({\bf T}_{\theta}\times {\bf T}_{\phi})&=&(x{\bf i}+y{\bf j}+z{\bf k}) \, {\cdot}\, ({\bf T}_{\theta}\times {\bf T}_{\phi})\\ &=&[(\cos\theta\sin\phi){\bf i}+(\sin\theta\sin\phi){\bf j}+(\cos\phi){\bf k}]\\ && {\cdot}\,({-}\sin\phi)[(\sin\phi\cos\theta){\bf i}+(\sin\phi\sin\theta){\bf j}+(\cos\phi) {\bf k}]\\ &=&({-}\sin\phi)(\sin^2\phi\cos^2\theta+\sin^2\phi\sin^2\theta+\cos^2\phi) ={-}\sin\phi.\\[-19pt] \end{eqnarray*}
Thus, \[ \int\!\!\!\int\nolimits_{\Phi}{\bf r}\, {\cdot} \, \,d{\bf S}=\int\!\!\!\int\nolimits_{D}-\sin\phi \,d\phi \,d\theta=\int^{2\pi}_0(-2) \,d\theta=-4\pi. \]
Orientation
An analogy can be drawn between the surface integral \({\int\!\!\!\int}_{\Phi}{\bf F}\,{\cdot}\, d{\bf S}\) and the line integral \(\int_{\bf c}{\bf F}\,{\cdot}\,d{\bf s}\). Recall that the line integral is an oriented integral. We needed the notion of orientation of a curve to extend the definition of \(\int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s}\) to line integrals \(\int_C{\bf F}\, {\cdot} \,d{\bf s}\) over oriented curves. We extend the definition of \(\int\!\!\!\int\nolimits_{\Phi}{\bf F}\, {\cdot}\,d{\bf S}\) to oriented surfaces in a similar fashion; that is, given a surface \(S\) parametrized by a mapping \({\Phi}\), we want to define \(\int\!\!\!\int\nolimits_{ S}{\bf F}\, {\cdot} \,d{\bf S} ={\int\!\!\!\int}_{\Phi}{\bf F}\, {\cdot} \,d{\bf S}\) and show that it is independent of the parametrization, except possibly for the sign. To accomplish this, we need the notion of orientation of a surface.
402
Definition: Oriented Surfaces
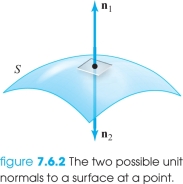
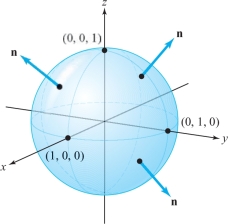
An oriented surface is a two-sided surface with one side specified as the outside or positive side; we call the other side the inside or negative side.footnote # At each point \((x, y, z)\in S\) there are two unit normal vectors \({\bf n}_1\) and \({\bf n}_2\), where \({\bf n}_1 = -{\bf n}_2\) (see Figure 17.42). Each of these two normals can be associated with one side of the surface. Thus, to specify a side of a surface \(S\), at each point we choose a unit normal vector \({\bf n}\) that points away from the positive side of \(S\) at that point.
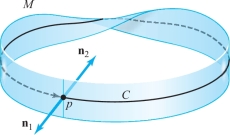
This definition assumes that our surface does have two sides. In fact, this is necessary, because there are examples of surfaces with only one side! The first known example of such a surface was the Möbius strip (named after the German mathematician and astronomer A. F. Möbius, who, along with the mathematician J. B. Listing, discovered it in 1858). Pictures of such a surface are given in Figure 17.43 and Figure 17.44. At each point of \(M\) there are two unit normals, \({\bf n}_1\) and \({\bf n}_2\). However, \({\bf n}_1\) does not determine a unique side of \(M\), and neither does \({\bf n}_2\). To see this intuitively, we can slide \({\bf n}_2\) around the closed curve \(C\) (Figure 17.43). When \({\bf n}_2\) returns to a fixed point \(p\) on \(C\) it will coincide with \({\bf n}_1\), showing that both \({\bf n}_1\) and \({\bf n}_2\) point away from the same side of \(M\) and, consequently, that \(M\) has only one side.
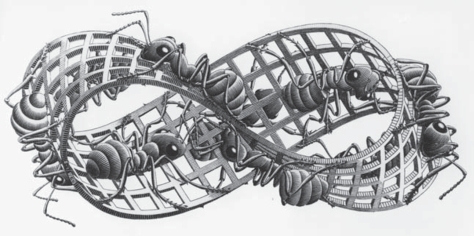
Figure 17.44 is a Möbius strip as drawn by the well-known twentieth-century mathematician and artist M. C. Escher. It depicts ants crawling along the Möbius band. After one trip around the band (without crossing an edge) they end up on the “opposite side” of the surface.
403
Let \({\Phi}\colon\, D\to {\mathbb R}^3\) be a parametrization of an oriented surface \(S\) and suppose \(S\) is regular at \({\Phi}(u_0,v_0),(u_0,v_0)\in D \); thus, the vector \(({\bf T}_{u_0}\times {\bf T}_{v_0})/\|{\bf T}_{u_0}\times {\bf T}_{v_0}\|\) is defined. If \({\bf n}({\Phi}(u_0,v_0))\) denotes the unit normal to \(S\) at \({\Phi}(u_0,v_0)\), it follows that \[ ({\bf T}_{u_0}\times {\bf T}_{v_0})/\|{\bf T}_{u_0}\times {\bf T}_{v_0}\|=\pm {\bf n}({\Phi}(u_0,v_0)). \]
The parametrization \({\Phi} \) is said to be orientation-preserving if we have the \(+\) sign; that is, if \(({\bf T}_{u}\times {\bf T}_{v})/\|{\bf T}_{u}\times {\bf T}_{v}\|= {\bf n}({\Phi}(u,v))\) at all \((u,v)\in D\) for which \(S\) is smooth at \({\Phi}(u,v)\). In other words, \({\Phi}\) is orientation-preserving if the vector \({\bf T}_u\times {\bf T}_v\) points to the outside of the surface. If \({\bf T}_u\times {\bf T}_v\) points to the inside of the surface at all points \((u,v)\in D\) for which \(S\) is regular at \({\Phi}(u,v)\), then \({\Phi}\) is said to be orientation-reversing. Using the preceding notation, this condition corresponds to the choice \(({\bf T}_{u}\times {\bf T}_{v})/\|{\bf T}_{u}\times {\bf T}_{v}\|= -{\bf n}({\Phi}(u,v))\).
It follows from this discussion that the Möbius band \(M\) cannot be parametrized by a single parametrization for which \({\bf n}={\bf T}_u \times {\bf T}_v \neq {\bf 0}\) and \({\bf n}\) is continuous over the whole surfacefootnote # (if there were such a parameterization, then \(M\) would indeed have two sides, one determined by \({\bf n}\) and one determined by \(-{\bf n}\)). The sphere in Example 1 can be parametrized by a single parametrization, but not by one that is everywhere one-to-one—see the discussion at the beginning of Section 17.4.
Thus, any one-to-one parametrized surface for which \({\bf T}_u \times {\bf T}_v\) never vanishes can be considered as an oriented surface with a positive side determined by the direction of \({\bf T}_u \times {\bf T}_v\).
example 2
We can give the unit sphere \(x^2 + y^2 + z^2 = 1\) in \({\mathbb R}^3\) (Figure 17.45) an orientation by selecting the unit vector \({\bf n}(x,y,z) = {\bf r}\), where \({\bf r}=x{\bf i}+y{\bf j}+z{\bf k}\), which points to the outside of the surface. This choice corresponds to our intuitive notion of outside for the sphere.
Now that the sphere \(S\) is an oriented surface, consider the parametrization \({\Phi}\) of \(S\) given in Example 1. The cross product of the tangent vectors \({\bf T}_{\theta}\) and \({\bf T}_{\phi} \)—that is, a normal to \(S\) is given by \[ ({-}\sin\phi)[(\cos\theta\sin\phi){\bf i}+(\sin\theta\sin\phi){\bf j}+ (\cos\phi){\bf k}]=-{\bf r}\sin\phi. \]
404
Because \(-{\sin} \, \phi\leq 0 \hbox{ for } 0\leq \phi \leq \pi\), this normal vector points inward from the sphere. Thus, the given parametrization \({\Phi} \) is orientation-reversing. By swapping the order of \(\theta\) and \(\phi\), we would get an orientation-preserving parametrization.
Orientation and the Vector Surface Element of a Sphere
Consider the sphere of radius \(R\), namely, \(x^{2}+y^{2}+z^{2}=R^{2}\). It is standard practice to orient the sphere with the outward unit normal. In terms of the position vector \({\bf r} = x{\bf i} + y{\bf j} + z{\bf k}\), the outward unit normal is given by \[ {\bf n}=\frac{{\bf r}}{R}. \]
The order of spherical coordinates that goes along with this orientation, as is evident from Example 2, is given by the order (\(\phi\), \(\theta )\). The computation in Example 2 shows that the surface-area element is then given by \[ d{\bf S} = {\bf n} \ {\cdot} \ ({\bf T}_{\phi} \times {\bf T}_{\theta}) \, d\phi\, d\theta = {\bf r}R \sin\phi\, d\phi \, d\theta = {\bf n} R^2 \sin \phi\, d\phi\, d\theta. \]
Question 17.145 Section 17.6 Progress Check Question #1
The surface element for the sphere \(x^2+y^2+z^2=R^2\) is given by \[\displaystyle d{\bf S} = (x{\bf i} + y {\bf j} + z {\bf k}) R \sin \phi \ d\phi \ d\theta \] wheras the surface element for the sphere \(x^2+y^2+z^2=R^2\) is given by \[\displaystyle dS = R^{2} \sin \phi \ d\phi \ d\theta.\]
The Orientation of Graphs
The next example discusses the orientation conventions for graphs. We shall compute the area element on graphs later in this section.
example 3
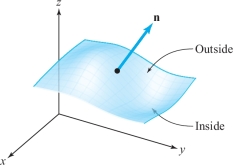
Let \(S\) be a surface described by \(z = g(x, y)\). As in equation (6), Section 17.5, there are two unit normal vectors to \(S\) at \((x_0, y_0, g(x_0, y_0))\), namely, \(\pm {\bf n}\), where \[ {\bf n}=\frac{\displaystyle -\frac{\partial g}{\partial x} (x_0,y_0){\bf i}-\displaystyle \frac{\partial g}{\partial y} (x_0,y_0){\bf j}+{\bf k}} {\sqrt{\bigg[\displaystyle \frac{\partial g}{\partial x}(x_0,y_0)\bigg]^2+ \bigg[\displaystyle \frac{\partial g}{\partial y}(x_0,y_0)\bigg]^2+1}}. \]
We can orient all such surfaces by taking the positive side of \(S\) to be the side away from which \({\bf n}\) points (Figure 17.46). Thus, the positive side of such a surface is determined by the unit normal \({\bf n}\) with positive \({\bf k}\) component—that is, it is upward-pointing. If we parametrize this surface by \({\Phi} (u,v) = (u,v, g(u,v))\), then \({\Phi}\) will be orientation-preserving.
Independence of Parametrization
405
We now state without proof a theorem showing that the integral over an oriented surface is independent of the parametrization. The proof of this theorem is analogous to that of Theorem 1 (Section 17.2); the heart of the proof is again the change of variables formula—this time applied to double integrals.
Theorem 4 \(\ \)Independence of Surface Integrals on Parametrizations
Let \(S\) be an oriented surface and let \({\Phi}_1\) and \({\Phi}_2\) be two regular orientation-preserving parametrizations, with \({\bf F}\) a continuous vector field defined on \(S\). Then \[ \int\!\!\!\int\nolimits_{{\Phi}_1}{\bf F}\, {\cdot} \,d{\bf S} =\int\!\!\!\int\nolimits_{{\Phi}_2}{\bf F}\, {\cdot} \,d{\bf S} . \]
If \({\Phi}_1\) is orientation-preserving and \({\Phi}_2\) orientation-reversing, then \[ \int\!\!\!\int\nolimits_{{\Phi}_1}{\bf F}\, {\cdot} \,d{\bf S} =-\int\!\!\!\int\nolimits_{{\Phi}_2}{\bf F}\, {\cdot} \,d{\bf S} . \]
If \(f\) is a real-valued continuous function defined on \(S\), and if \({\Phi}_1\) and \({\Phi}_2\) are parametrizations of \(S\), then \[ \int\!\!\!\int\nolimits_{{\Phi}_1}f d S=\int\!\!\!\int\nolimits_{{\Phi}_2}fd S. \]
Note that if \(f = 1\), we obtain \[ A(S)=\int\!\!\!\int\nolimits_{{\Phi}_1} d S=\int\!\!\!\int\nolimits_{{\Phi}_2}d S, \] thus showing that area is independent of parametrization.
We can therefore unambiguously use the notation \[ \int\!\!\!\int\nolimits_{S}{\bf F}\, {\cdot} \,d{\bf S} =\int\!\!\!\int\nolimits_{{\Phi}}{\bf F}\, {\cdot} \,d{\bf S} \] (or a sum of such integrals, if \(S\) is a union of parametrized surfaces that intersect only along their boundary curves) where \({\Phi}\) is an orientation-preserving parametrization. Theorem 4 guarantees that the value of the integral does not depend on the selection of \({\Phi}\).
Relation with Scalar Integrals
Recall from formula (1) of Section 17.2 that a line integral \(\int_{{\bf c}}{\bf F}\, {\cdot} \,d{\bf s}\) can be thought of as the path integral of the tangential component of \({\bf F}\) along \({\bf c}\) (although for the case in which \({\bf c}\) intersects itself, the integral obtained is technically not a path integral). A similar situation holds for surface integrals, because we are assuming that the mappings \({\Phi}\) defining the surface \(S\) are one-to-one, except perhaps on the boundary of \(D\), which can be ignored for the purposes of integration. Thus, in defining integrals over surfaces, we assume in this book that the surfaces are nonintersecting.
406
For an oriented smooth surface \(S\) and an orientation-preserving parametrization \({\Phi}\) of \(S\), we can express \({\int\!\!\!\int}_S{\bf F}\, {\cdot} \,d{\bf S}\) as an integral of a real-valued function \(f\) over the surface. Let \({\bf n}=({\bf T}_u\times {\bf T}_v)/ \|{\bf T}_u\times {\bf T}_v\|\) be the unit normal pointing to the outside of \(S\). Then \begin{eqnarray*} \int\!\!\!\int\nolimits_{S}{\bf F}\, {\cdot} \,d{\bf S} &=&\int\!\!\!\int\nolimits_{{\Phi}} {\bf F}\, {\cdot} \,d{\bf S} = \int\!\!\!\int\nolimits_{D} {\bf F}\, {\cdot}\, ({\bf T}_u\times {\bf T}_v)\,du\,dv\\[4pt] &=&\int\!\!\!\int\nolimits_{D}{\bf F}\, {\cdot}\, \bigg(\frac{{\bf T}_u\times {\bf T}_v}{\|{\bf T}_u\times {\bf T}_v\|}\bigg)\| {\bf T}_u\times {\bf T}_v\|\,du\,dv\\[4pt] &=&\int\!\!\!\int\nolimits_{D}({\bf F}\, {\cdot}\, {\bf n})\| {\bf T}_u\times {\bf T}_v\|\,du\, dv =\int\!\!\!\int\nolimits_{S} ({\bf F}\, {\cdot}\, {\bf n})\,dS =\int\!\!\!\int\nolimits_{S} f \,dS,\\[-14.3pt] \end{eqnarray*} where \(f={\bf F}\, {\cdot} \,{\bf n}\). We have thus proved the following theorem.
Theorem 5
\({\int\!\!\!\int}_{S}{\bf F}\, {\cdot} \,d{\bf S}\), the surface integral of \({\bf F}\) over \(S\), is equal to the integral of the normal component of\ {\bf \ F} over the surface. In short, \[ \int\!\!\!\int\nolimits_{S} {\bf F}\, {\cdot} \,d{\bf S} =\int\!\!\!\int\nolimits_{S}{\bf F}\, {\cdot}\,{\bf n} \,dS. \]
The observation in Theorem 5 can often save computational effort, as Example 4 demonstrates.
The Physical Interpretation of Surface Integrals
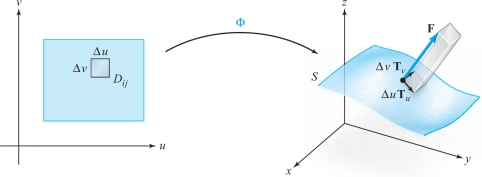
The geometric and physical significance of the surface integral can be understood by expressing it as a limit of Riemann sums. For simplicity, we assume \(D\) is a rectangle. Fix a parametrization \({\Phi}\) of \(S\) that preserves orientation and partition the region \(D\) into \(n^2\) pieces \(D_{\it ij},0\leq i\leq n-1,0\leq j\leq n-1\). We let \({\Delta} u\) denote the length of the horizontal side of \(D_{\it ij}\) and \({\Delta} v\) denote the length of the vertical side of \(D_{\it ij}\). Let \((u, v)\) be a point in \(D_{\it ij}\), and \((x, y, z)={\Phi}(u,v)\) the corresponding point on the surface. We consider the parallelogram with sides \({\Delta} u \,{\bf T}_u\) and \({\Delta} v\, {\bf T}_v\) lying in the plane tangent to \(S\) at \((x, y, z)\) and the parallelepiped formed by \({\bf F}\), \({\Delta} u\,{\bf T}_u\), and \({\Delta} v\,{\bf T}_v\). The volume of the parallelepiped is the absolute value of the triple product \[ {\bf F}\, {\cdot}\, ( { \Delta} u\, {\bf T}_u\times { \Delta} v\, {\bf T}_v)={\bf F} \, {\cdot}\, ({\bf T}_u\times {\bf T}_v) {\, \Delta} u \,{ \Delta} v. \]
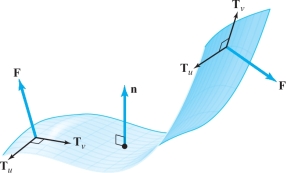
The vector \({\bf T}_u\times {\bf T}_v\) is normal to the surface at \((x, y, z)\) and points away from the outside of the surface. Thus, the number \({\bf F}\, {\cdot}\, ({\bf T}_u\times {\bf T}_v)\) is positive when the parallelepiped lies on the outside of the surface (Figure 17.47).
In general, the parallelepiped lies on that side of the surface away from which \({\bf F}\) is pointing. If we think of \({\bf F}\) as the velocity field of a fluid, \({\bf F}(x, y, z)\) is pointing in the direction in which fluid is moving across the surface near \((x, y, z)\). Moreover, the number \[ |{\bf F}\, {\cdot}\, ({\bf T}_u \,{ \Delta} u\times {\bf T}_v\, { \Delta} v)| \] measures the amount of fluid that passes through the tangent parallelogram per unit time. Because the sign of \({\bf F}\, {\cdot}\, ( { \Delta} u\, {\bf T}_u\times { \Delta} v\,{\bf T}_v)\) is positive if the vector \({\bf F}\) is pointing outward at \((x, y, z)\) and negative if \({\bf F}\) is pointing inward, \({\textstyle\sum}_{i,j}{\bf F}\, {\cdot}\, ({\bf T}_u\times {\bf T}_v)\, {\Delta} u \,{ \Delta} v\) is an approximate measure of the net quantity of fluid to flow outward across the surface per unit time. (Remember that “outward” or “inward” depends on our choice of parametrization. Figure 17.48 illustrates \({\bf F}\) directed outward and inward, given \({\bf T}_u\) and \({\bf T}_v\).) Hence, the integral \({\int\!\!\!\int}_S{\bf F}\, {\cdot} \,d{\bf S}\) is the net quantity of fluid to flow across the surface per unit time, that is, the rate of fluid flow. This integral is also called the flux of \({\bf F}\) across the surface.
407
In the case where \({\bf F}\) represents an electric or a magnetic field, \({\int\!\!\!\int}_S{\bf F}\, {\cdot} \,d{\bf S}\) is also commonly known as the flux. The reader may be familiar with physical laws (such as Faraday’s law) that relate flux of a vector field to a circulation (or current) in a bounding loop. This is the historical and physical basis of Stokes’ theorem, which we will discuss in Section 18.2. The corresponding principle in fluid mechanics is called Kelvin’s circulation theorem.
Question 17.146 Section 17.6 Progress Check Question #2
Let \(S\) be the closed surface that consists of the hemisphere \(x^2+y^2+z^2=1, z \geq 0\) and its base \(x^2+y^2 \leq 1, z=0\). Let \({\bf E}\) be the electric field defined by \({\bf E}= 2x {\bf i} + 2y {\bf j} + 2z {\bf k}\). Find the electric flux across \(S\).
| A. |
| B. |
| C. |
| D. |
| E. |
Surface integrals also apply to the study of heat flow. Let \(T(x, y, z)\) be the temperature at a point \((x, y, z)\in W\subset {\mathbb R}^3\), where \(W\) is some region and \(T\) is a \(C^1\) function. Then \[ \nabla T=\frac{\partial T}{\partial x}{\bf i}+ \frac{\partial T}{\partial y}{\bf j}+ \frac{\partial T}{\partial z}{\bf k} \] represents the temperature gradient, and heat “flows” with the vector field \(-k\, \nabla T\,{=}\,{\bf F}\), where \(k\) is a positive constant (see Section 18.5). Therefore, \({\int\!\!\!\int}_S{\bf F}\, {\cdot} \,d{\bf S}\) is the total rate of heat flow or flux across the surface \(S\).
example 4
Suppose a temperature function is given in \({\mathbb R}^3\) by the formula \(T(x, y, z) = x^2 + y^2 + z^2\), and let \(S\) be the unit sphere \(x^2 + y^2 + z^2 = 1\) oriented with the outward normal (see Example 2). Find the heat flux across the surface \(S\) if \(k=1\).
solution We have \[ {\bf F}=-\nabla T(x,y,z)=-2x{\bf i}-2y{\bf j}-2z{\bf k}. \]
408
On \(S\), the vector \({\bf n}(x, y, z) = x{\bf i} + y{\bf j} + z{\bf k}\) is the unit “outward” normal to \(S\) at \((x, y, z)\), and \(f(x, y, z) = {\bf F}\, {\cdot}\, {\bf n} = - 2x^2 - 2y^2 - 2z^2 = - 2\) is the normal component of \({\bf F}\). From Theorem 5 we can see that the surface integral of \({\bf F}\) is equal to the integral of its normal component \(f={\bf F}\, {\cdot}\, {\bf n}\) over \(S\). Thus, \[ \int\!\!\!\int\nolimits_{S}{\bf F}\, {\cdot}\, \,d{\bf S} =\int\!\!\!\int\nolimits_{S} f \,dS=-2\int\!\!\!\int\nolimits_{S}\,dS=-2A(S)=-2(4\pi)=-8\pi. \]
The flux of heat is directed toward the center of the sphere (why toward?). Clearly, our observation that \({\int\!\!\!\int}_S{\bf F}\, {\cdot}\, \,d{\bf S} ={\int\!\!\!\int}_Sf \,dS\) has saved us considerable computational time.
In this example, \({\bf F}(x, y, z) = -2x{\bf i} - 2y{\bf j} - 2z{\bf k}\) could also represent an electric field, in which case \({\int\!\!\!\int}_S{\bf F}\, {\cdot}\, \,d{\bf S} =-8\pi\) would be the electric flux across \(S\).
example 5
Gauss’ Law There is an important physical law, due to the great mathematician and physicist K. F. Gauss, that relates the flux of an electric field \({\bf E}\) over a “closed” surface \(S\) (e.g., a sphere or an ellipsoid) to the net charge \(Q\) enclosed by the surface, namely (in suitable units), \begin{equation*} \int\!\!\!\int\nolimits_{S} {\bf E}\, {\cdot} \,d{\bf S} =Q\tag{1} \end{equation*} (see Figure 17.49). Gauss’ law will be discussed in detail in Chapter 18. This law is analogous to Ampère’s law (see Example 12, Section 17.2).
Suppose that \({\bf E} = E{\bf n} \); that is, \({\bf E}\) is a constant scalar multiple of the unit normal to \(S\). Then Gauss’ law, equation (1) in Example 5, becomes \[ \int\!\!\!\int\nolimits_{S}{\bf E}\, {\cdot} \,d{\bf S} =\int\!\!\!\int\nolimits_{S} E\,dS =E \int\!\!\!\int\nolimits_{S} \,dS=Q \] because \(E = {\bf E}\, {\cdot}\, {\bf n}\). Thus, \begin{equation*} E=\frac{Q}{A(S)}.\tag{2} \end{equation*}
In the case where \(S\) is the sphere of radius \(R\), equation \((2)\) becomes \begin{equation*} E=\frac{Q}{4\pi\! R^2}\tag{3} \end{equation*} (see Figure 17.50).
Now suppose that \({\bf E}\) arises from an isolated point charge, \(Q\). From symmetry it is reasonable that \({\bf E} = E{\bf n}\), where \({\bf n}\) is the unit normal to any sphere centered at \(Q\). Hence, equation \((3)\) holds. Consider a second point charge, \(Q_0\), located at a distance \(R\) from \(Q\). The force \({\bf F}\) that acts on this second charge, \(Q_0\), is given by \[ {\bf F}={\bf E}Q_0=EQ_0{\bf n}=\frac{Q\! Q_0}{4\pi \!R^2}{\bf n}. \]
If \(F\) is the magnitude of \({\bf F}\), we have \[ F=\frac{Q\! Q_0}{4\pi\! R^2}, \] which is Coulomb’s law for the force between two point charges.footnote #
409

Surface Integrals Over Graphs
Finally, let us derive the surface-integral formulas for vector fields \({\bf F}\) over surfaces \(S\) that are graphs of functions.
Consider the surface \(S\) described by \(z = g(x, y)\), where \((x, y) \in D\), where \(S\) is oriented with the upward-pointing unit normal: \[ {\bf n}=\frac{\displaystyle -\frac{\partial g}{\partial x} {\bf i}-\displaystyle \frac{\partial g}{\partial y}{\bf j}+{\bf k}} {\sqrt{\bigg(\displaystyle \frac{\partial g} {\partial x}\bigg)^2+\bigg(\displaystyle \frac{\partial g}{\partial y}\bigg)^2}+1}. \]
We have seen that we can parametrize \(S\) by \({\Phi}\colon\, D\to {\mathbb R}^3\) given by \({\Phi}(x,y)= (x,y,g(x,y))\). In this case, \({\int\!\!\!\int}_S{\bf F}\,{\cdot}\,d{\bf S}\) can be written in a particularly simple form. We have \[ {\bf T}_x={\bf i}+\frac{\partial g}{\partial x}{\bf k},\qquad\! {\bf T}_y={\bf j}+\frac{\partial g}{\partial y}{\bf k}. \]
Thus, \({\bf T}_x\times {\bf T}_y=-(\partial g/\partial x){\bf i}-(\partial g/\partial y){\bf j}+ {\bf k}\). If \({\bf F}=F_1{\bf i} + F_2{\bf j} + F_3{\bf k}\) is a continuous vector field, then we get
410
The Surface Integral of a Vector Field Over a Graph \(S\)
\begin{equation*} \begin{array}{lll} \int\!\!\!\int\nolimits_{S}{\bf F}\, {\cdot} \,d{\bf S} &=&\int\!\!\!\int\nolimits_{D} {\bf F}\,{\cdot}\,({\bf T}_x\times {\bf T}_y)\,{\it dx} \,{\it dy} \\[-1pt] &=&\int\!\!\!\int\nolimits_{D}\bigg[F_1\bigg({-}\frac{\partial g}{\partial x}\bigg)+ F_2\bigg({-}\frac{\partial g}{\partial y}\bigg)+F_3\bigg]{\it dx} \,{\it dy} . \end{array}\tag{4} \end{equation*}
example 6
The equations \[ z=12,\qquad x^2+y^2\leq 25 \] describe a disc of radius 5 lying in the plane \(z = 12\). Suppose \({\bf r}\) is the vector field \[ {\bf r}(x,y,z)=x{\bf i} + y{\bf j}+z {\bf k}. \]
Compute \({\int\!\!\!\int}_S{\bf r}\,{\cdot}\,d{\bf S}\).
solution We shall do this in three ways. First, we have \(\partial z/\partial x=\partial z/\partial y=0\), because \(z =12\) is constant on the disc, so \[ {\bf r}(x,y,z)\, {\cdot}\, ({\bf T}_x\times {\bf T}_y)={\bf r}(x,y,z)\, {\cdot}\, ({\bf i} \times {\bf j})={\bf r}(x,y,z){\, {\cdot}\, } {\bf k}=z. \]
Using the original definition at the beginning of this section, the integral becomes \[ \int\!\!\!\int\nolimits_{S}{\bf r}\, {\cdot} \,d{\bf S} =\int\!\!\!\int\nolimits_{D} z \,{\it dx}\,{\it dy}=\int\!\!\!\int\nolimits_{D} 12 \,{\it dx} \,{\it dy} =12(\hbox{area of }D)=300\pi. \]
A second solution: Because the disc is parallel to the \({\it xy}\) plane, the outward unit normal is \({\bf k}\). Hence, \({\bf n}(x, y, z) = {\bf k}\) and \({\bf r}\, {\cdot}\, {\bf n}=z\). However, \(\|{\bf T}_x\times {\bf T}_y\|=\|{\bf k}\|=1\), and so we know from the discussion preceding Theorem 5 that \[ \int\!\!\!\int\nolimits_{S}{\bf r}\, {\cdot} \,d{\bf S} =\int\!\!\!\int\nolimits_{S}{\bf r}\, {\cdot}\, {\bf n}\,\,dS=\int\!\!\!\int\nolimits_{S} z \, \,dS=\int\!\!\!\int\nolimits_{D} 12 \,{\it dx} \,{\it dy} =300\pi. \]
Third, we may solve this problem by using formula (4) directly, with \(g(x, y) = 12\) and \(D\) the disc \(x^2 + y^2\leq 25 \): \[ \int\!\!\!\int\nolimits_{S} {\bf r}\, {\cdot} \,d{\bf S} = \int\!\!\!\int\nolimits_{D} (x \,{\cdot}\,0 + y \,{\cdot}\,0+ 12) \,{\it dx} \,{\it dy} =12 \hbox{(area of } D) = 300 \pi. \]
Question 17.147 Section 17.6 Progress Check Question #3
Which of the following statements are true?
(i) Every surface is orientable.
(ii) The vector surface integral of the vector field \({\bf F}\), \( \int\!\!\!\int\nolimits_{S} {\bf F}\, {\cdot} \,d{\bf S} \), is equal to the scalar surface integral of the normal component of \({\bf F}\), \(\int\!\!\!\int\nolimits_{S}{\bf F}\, {\cdot}\,{\bf n} \,dS. \)
(iii) If \({\bf \Phi}_1\) and \({\bf \Phi}_2\) are parameterizations of the same surface with the same orientation, then \( \int\!\!\!\int\nolimits_{{\bf \Phi}_1} {\bf F}\, {\cdot} \,d{\bf S}= \int\!\!\!\int\nolimits_{{\bf \Phi}_2} {\bf F}\, {\cdot} \,d{\bf S} \)
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
| G. |
Summary: Formulas for Surface Integrals
- 1. Parametrized Surface: \({\Phi} (u, v)\)
- a. Integral of a scalar function \(f\): \[ \int\!\!\!\int\nolimits_{S} f dS = \int\!\!\!\int\nolimits_{D} f ({\Phi} (u, v)) \| {\bf T}_{u} \times {\bf T}_{v}\| \,du\,dv \]
- b. Scalar surface element: \[ dS = \|{\bf T}_{u} \times {\bf T}_{v}\|\,du \, dv \]
- c. Integral of a vector field \({\bf F}\): \[ \int\!\!\!\int\nolimits_{S} {\bf F} \,{\cdot}\,d {\bf S} = \int\!\!\!\int\nolimits_{D} {\bf F}\,{\cdot}\,({\bf T}_{u} \times {\bf T}_{v})\, du\, dv \]
- d. Vector surface element: \[ d{\bf S} = ({\bf T}_{u} \times {\bf T}_{v})\, du\, dv = {\bf n}\ dS \]
- 2. Graph: \(z=g(x, y)\)
- a. Integral of a scalar function \(f\): \[ \int\!\!\!\int\nolimits_S f\, dS = \int\!\!\!\int\nolimits_D \frac{f(x,y, g(x,y))}{\cos\theta}\,{\it dx}\,{\it dy} \]
- b. Scalar surface element: \[ dS = \frac{{\it dx}\, {\it dy}}{\cos \theta}= \sqrt{\left(\frac{\partial g}{\partial x}\right)^2 + \left(\frac{\partial g}{\partial y}\right)^2 + 1}\,{\it dx}\,{\it dy}, \] where \(\cos\, \theta = {\bf n}\ {\cdot}\ {\bf k}\), and \({\bf n}\) is a unit normal vector to the surface.
- c. Integral of a vector field \({\bf F}\): \[ \int\!\!\!\int\nolimits_S {\bf F} \ {\cdot} \ d{\bf S} = \int\!\!\!\int\nolimits_D \left( -F_1 \frac{\partial g}{\partial x} - F_2\frac{\partial g}{\partial y} + F_3 \right){\it dx}\,{\it dy} \]
- d. Vector surface element: \[ d{\bf S} = {\bf n} \ {\cdot} \ dS = \left(-\frac{\partial g}{\partial x}{\bf i}- \frac{\partial g}{\partial y}{\bf j} + {\bf k}\right) {\it dx}\,{\it dy} \]
- 3. Sphere: \(x^{2}+y^{2}+z^{2}=R^{2}\)
- a. Scalar surface element: \[ dS = R^{2} \sin \phi \, d\phi \, d\theta \]
- b. Vector surface element: \[ d{\bf S} = (x{\bf i} + y {\bf j} + z {\bf k}) R \sin \phi \, d\phi \, d\theta = {\bf r} R \sin \phi \, d\phi \, d\theta = {\bf n} R^2 \sin \phi \, d\phi \, d\theta \]