Question 17.3

The curve \(C\), which goes along the circle of radius 3, from the point \((3,0)\) to the point \((-3,0)\), and then in a straight line along the \(x\)-axis back to \((3,0)\)

Question 17.4

The curve \(C\), which goes along \(y=x^2\) from the point \((0,0)\) to the point \((2,4)\), then in a straight line from \((2,4)\) to \((0,4)\), and then along the \(y\)-axis back to \((0,0)\)

Question 17.5

The curve \(C\), which goes along \(y= \sin x\) from the point \((0,0)\) to the point \((\pi, 0)\), and then along the \(x\)-axis back to \((0,0)\)

Question 17.6

The closed curve \(C\) described by the ellipse \[ \frac{(x-2)^{2}}{4} + \frac{(y-3)^{2}}{9} = 1 \] oriented counterclockwise

Question 17.7

The intersection of the plane \(z=3\) with the elliptical cylinder \[ \frac{x^2}{9} + \frac{y^2}{16} = 1 \]

Question 17.8

The triangle formed by traveling from the point \((1,2,3)\) to \((0,-2,1)\), to \((6,4,2)\), and back to \((1,2,3)\)

Question 17.9

The intersection of the surfaces \(y=x\) and \(z=x^3\), from the point \((-3,-3,9)\) to \((2,2,4)\)

Question 17.10

The intersection of the cylinder \(y^2 + z^2 = 1\) and the plane \(z=x\)

Question 17.11

Let \(f(x,y,z) = y\) and \({\bf c}(t) = (0,0,t), 0 \leq t \leq 1\). Prove that \(\int_{\bf c}f \,{\it ds} = 0\).

Question 17.12

Evaluate the following path integrals \(\int_{\bf c}f(x,y,z) \ {\it ds}\), where

• (a) \(f(x,y,z) = x+ y +z\) and \({\bf c}\colon\, t \mapsto (\sin t,\cos t, t), t \in [0,2\pi]\)
• (b) \(f(x,y,z) = \cos z, {\bf c}\) as in part (a)

Question 17.13

Evaluate the following path integrals \(\int_{\bf c} f(x,y,z) \,{\it ds}\), where

• (a) \(f(x,y,z) = \exp \sqrt{z}\), and \({\bf c}\colon\, t \mapsto (1,2, t^2), t \in [0,1]\)
• (b) \(f(x,y,z) = yz\), and \({\bf c} \colon\, t \mapsto (t,3t, 2t), t \in [1,3]\)

Question 17.14

Evaluate the integral of \(f(x,y,z)\) along the path \({\bf c}\), where

• (a) \(f(x,y,z) = x\cos z\), \({\bf c}{:}\, t\mapsto t{\bf i} + t^2{\bf j}, t \in [0,1]\)
• (b) \(f(x,y,z) = (x+y)/(y+z)\), and \({\bf c}\colon\, t \mapsto \big(t,\frac{2}{3}t^{3/2}, t\big), t \in [1,2]\)

Question 17.15

Let \(f\colon\, {\mathbb R}^3\backslash \{ xz \hbox{ plane} \}\rightarrow {\mathbb R}\) be defined by \(f(x,y,z)=1/y^3\). Evaluate \(\int_{\bf c}f(x,y,z)\,{\it ds}\), where \({\bf c}\colon [1,e] \rightarrow {\mathbb R}^3\) is given by \({\bf c}(t) =(\log t) {\bf i} + t{\bf j} + 2 {\bf k}\).

357

Question 17.16

• (a) Show that the path integral of \(f(x, y)\) along a path given in polar coordinates by \(r = r(\theta)\), \(\theta_1 \leq \theta \leq \theta_2\), is \[ \int_{\theta_1}^{\theta_2} f(r \cos \theta, r \sin \theta) \sqrt{r^2 + \Big(\frac{dr}{d\theta}\Big)^2} d\theta. \]
• (b) Compute the arc length of the path \(r=1 + \cos \theta , 0 \leq \theta \leq 2 \pi\).

Question 17.17

Let \(f(x,y) = 2x - y\), and consider the path \(x = t^4, y = t^4, -1 \leq t \leq 1\).

• (a) Compute the integral of \(f\) along this path and interpret the answer geometrically.
• (b) Evaluate the arc-length function \(s(t)\) and redo part (a) in terms of \(s\) (you may wish to consult Exercise 2, Section 12.3).

Question 17.18

• (a) Justify the formula \([\int_{\bf c}f(x,y,z)\,{\it ds} ]/l({\bf c})\) for the average value of \(f\) along \({\bf c}\) using Riemann sums.
• (b) Show that the average value of \(f\) along \({\bf c}\) in Example 1 is \((1+ \frac{4}{3} \pi^2)\).
• (c) In the tenth exercise, parts (a) and (b) above, find the average value of \(f\) over the given curves.

Question 17.19

Find the average \(y\) coordinate of the points on the semicircle parametrized by \({\bf c}\colon\,[0,\pi]\rightarrow {\mathbb R}^3, \theta \mapsto (0 , a \sin \theta, a \cos \theta); a> 0\).

Question 17.20

Suppose the semicircle in the previous exercis is made of a wire with a uniform density of 2 grams per unit length.

• (a) What is the total mass of the wire?
• (b) Where is the center of mass of this configuration of wire? (Consult Section 16.3.)

Question 17.21

Let \({\bf c}\) be the path given by \({\bf c}(t)= (t^2, t, 3)\) for \(t \in [0,1]\).

• (a) Find \(l({\bf c})\), the length of the path.
• (b) Find the average \(y\) coordinate along the path \({\bf c}\).

Question 17.22

Show that the path integral of a function \(f(x,y)\) over a path \(C\) given by the graph of \(y=g(x)\), \(a \leq x \leq b\) is given by: \[ \int_{C} f \,{\it ds} = \int_{a}^{b} f(x,g(x)) \sqrt{1 + [g'(x)]^2} \,{\it dx} \]

Conclude that if \(g:[a,b] \rightarrow \mathbb R\) is piecewise continuously differentiable, then the length of the graph of \(g\) on \([a,b]\) is given by: \[ \int_{C} f \,{\it ds} = \int_{a}^{b} \sqrt{1 + g'(x)^2} \,{\it dx}. \]

Question 17.23

If \(g\colon\, [a,b]\rightarrow {\mathbb R}\) is piecewise continuously differentiable, let the length of the graph of \(g\) on \([a, b]\) be defined as the length of the path \(t \mapsto (t,g(t))\) for \(t \in [a,b]\).

Show that the length of the graph of \(g\) on \([a, b]\) is \[ \int^b_a \sqrt{1 + [g'(x)]^2} \,{\it dx}. \]

Question 17.24

Use the previous exercise to find the length of the graph of \(y = \log x\) from \(x=1\) to \(x=2\).

Question 17.25

Use an exercise above to evaluate the path integral of \(f(x,y)=y\) over the graph of the semicircle \(y = \sqrt{1-x^2}\), \(-1 \leq x \leq 1\).

Question 17.26

Compute the path integral of \(f(x,y)=y^2\) over the graph \(y = e^x\), \(0 \leq x \leq 1\).

Question 17.27

Compute the path integral of \(f(x,y,z)={\it xyz}\) over the path \(c(t) = (\cos t, \sin t, t)\), \(0 \leq t \leq \frac{\pi}{2}\).

Question 17.28

Find the mass of a wire formed by the intersection of the sphere \(x^2 + y^2 + z^2 =1\) and the plane \(x + y + z = 0\) if the density at \((x,y,z)\) is given by \(\rho(x,y,z) = x^2\) grams per unit length of wire.

358

Question 17.29

Evaluate \(\int_{\bf c}f \,{\it ds}\), where \(f(x,y,z) = z \) and \({\bf c}(t)=(t \cos t, t \sin t, t)\) for \(0 \leq t \leq t_0\).

Question 17.30

Write the following limit as a path integral of \(f(x,y, z) = {\it xy}\) over some path \({\bf c}\) on [0, 1] and evaluate: \[ {\displaystyle \mathop {\rm limit}_{N \rightarrow \infty}} \sum_{i=1}^{N-1} t_i^2 \big(t^2_{i+1} \,{-}\, t^2_i\big), \] where \(t_1,\ldots, t_N\) is a partition of \([0, 1]\).

Question 17.31

Consider paths that connect the points \(A = (0, 1)\) and \(B = (1, 0)\) in the xy plane, as in Figure 17.5.footnote #

Figure 17.5: A curve joining the points \(A\) and \(B\).

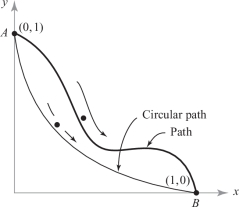
Galileo contemplated the following question: Does a bead falling under the influence of gravity from a point \(A\) to a point \(B\) along a curve do so in the least possible time if that curve is a circular arc? For any given path, the time of transit \(T\) is a path integral \[ T=\int\frac{{\it dt}}{v}, \] where the bead’s velocity is \(v=\sqrt{2{\it gy}}\), where \(g\) is the gravitational constant. In 1697, Johann Bernoulli challenged the mathematical world to find the path in which the bead would roll from \(A\) to \(B\) in the least time. This solution would determine whether Galileo’s considerations had been correct.

• (a) Calculate \(T\) for the straight-line path \(y = 1\,{-}\,x\).
• (b) Write a formula for \(T\) for Galileo’s circular path, given by (\(x- 1)^{2}\,{+}\, (y- 1)^{2} = 1\).

Incidentally, Newton was the first to send his solution [which turned out to be a cycloid—the same curve (inverted) that we studied in Section 12.1, Example 4], but he did so anonymously. Bernoulli was not fooled, however. When he received the solution, he immediately knew its author, exclaiming, “I know the Lion from his paw.” While the solution of this problem is a cycloid, it is known in the literature as the brachistrochrone. This was the beginning of the important field called the calculus of variations.