17.2 Line Integrals
We now consider the problem of integrating a vector field along a path. We will begin by considering the notion of work to motivate the general definition.
Work Done by Force Fields
If \({\bf F}\) is a force field in space, then a test particle (for example, a small unit charge in an electric force field or a unit mass in a gravitational field) will experience the force \({\bf F}\). Suppose the particle moves along the image of a path \({\bf c}\) while being acted upon by \({\bf F}\). A fundamental concept is the work done by \({\bf F}\) on the particle as it traces out the path \({\bf c}\). If \({\bf c}\) is a straight-line displacement given by the vector \({\bf d}\) and if \({\bf F}\) is a constant force, then the work done by \({\bf F}\) in moving the particle along the path is the dot product \({\bf F} \, {\cdot}\, {\bf d} \): \[ {\bf F} \, {\cdot}\, {\bf d} = (\hbox{magnitude of force}) \times (\hbox{displacement in direction of force}). \]
If the path is curved, we can imagine that it is made up of a succession of infinitesimal straight-line displacements or that it is approximated by a finite number of straight-line displacements. Then (as in our derivation of the formulas for the path integral in the preceding section) we are led to the following formula for the work done by the force field \({\bf F}\) on a particle moving along a path \({\bf c}\colon\, [a,b]\rightarrow {\mathbb R}^3 \): \[ \hbox{ work done by } {\bf F} = \int_a^b {\bf F}({\bf c}(t))\, {\cdot}\, {\bf c}' (t)\,{\it dt} . \]
359
We can further justify this derivation as follows. As \(t\) ranges over a small interval \(t\) to \(t +{ \Delta} t\), the particle moves from \({\bf c}(t)\) to \({\bf c}(t +{ \Delta} t)\), a vector displacement of \({\Delta} {\bf s} = {\bf c}(t +{ \Delta} t)- {\bf c}(t)\) (see Figure 17.6).
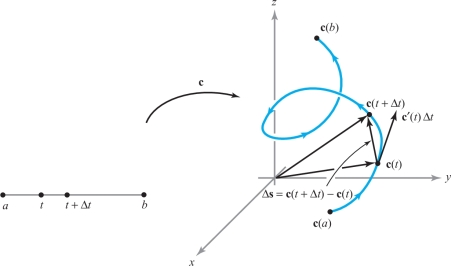
From the definition of the derivative, we get the approximation \({\Delta} {\bf s} \approx {\bf c}'(t){\Delta} t\). The work done in going from \({\bf c}(t)\) to \({\bf c}(t+{ \Delta} t)\) is therefore approximately \[ {\bf F}({\bf c}(t)) \, {\cdot}\, { \Delta} {\bf s} \approx {\bf F}({\bf c}(t)) \, {\cdot}\, {\bf c}'(t)\,{ \Delta} t. \]
If we subdivide the interval \([a, b]\) into \(n\) equal parts \(a = t_0 < t_1 < \cdots < t_n = b\), with \({\Delta} t = t_{i + 1} - t_i\), then the work done by \({\bf F}\) is approximately \[ \sum_{i=0}^{n-1} {\bf F}({\bf c}(t_i)) \, {\cdot}\, {\Delta}{\bf s} \approx \sum_{i=0}^{n-1} {\bf F}({\bf c}(t_i)) \, {\cdot}\, {\bf c}' (t_i) \,{ \Delta} t. \]
As \(n \rightarrow \infty\), this approximation becomes better and better, and so it is reasonable to take as our definition of work to be the limit of the sum just given as \(n \rightarrow \infty\). This limit is given by the integral \[ \int^b_a {\bf F}({\bf c}(t))\, {\cdot}\, {\bf c}'(t)\,{\it dt} . \]
Definition of the Line Integral
The previous discussion of work motivates the following definition.
Definition: Line Integrals
Let \({\bf F}\) be a vector field on \({\mathbb R}^3\) that is continuous on the \(C^1\) path \({\bf c}\colon\, [a,b] \rightarrow {\mathbb R}^3\). We define \(\int_{\bf c}{\bf F} \, {\cdot}\,d{\bf s}\), the line integral of \({\bf F}\) along \({\bf c}\), by the formula \[ \int_{\bf c} {\bf F} \, {\cdot} \,d{\bf s} = \int^b_a {\bf F}({\bf c}(t)) \, {\cdot}\, {\bf c}'(t) \,{\it dt}; \] that is, we integrate the dot product of \({\bf F}\) with \({\bf c}'\) over the interval \([a, b]\).
As is the case with scalar functions, we can also define \(\int_{\bf c}{\bf F} \, {\cdot} \,d{\bf s}\) if \({\bf F}({\bf c}(t)) \, {\cdot}\, {\bf c}'(t)\) is only piecewise continuous.
360
For paths \({\bf c}\) that satisfy \({\bf c}'(t)\neq {\bf 0}\), there is another useful formula for the line integral: namely, if \({\bf T}(t)= {\bf c}'(t)/ \|{\bf c}'(t)\|\) denotes the unit tangent vector, we have \begin{equation} \begin{array}{rlll} \int {\bf F} \, {\cdot} \,d{\bf s} &=& \int^b_a {\bf F} ({\bf c} (t) ) \, {\cdot}\,{\bf c}' (t)\,{\it dt}&\hbox{(by definition)}\\[4pt] &=& \int^b_a \bigg[ {\bf F} ({\bf c} (t)) \, {\cdot}\, \frac{{\bf c}'(t)}{\| {\bf c}'(t)\|}\bigg] \| {\bf c}'(t) \| \,{\it dt}& \hbox{(canceling }\| {\bf c}'(t)\| \hbox{)}\\[4pt] &=& \displaystyle\int^b_a [ {\bf F}({\bf c}(t)) \, {\cdot}\, {\bf T}(t)]\| {\bf c}' (t)\| \,{\it dt}.& \end{array} \end{equation}
This formula says that \(\int_{\bf c} {\bf F}\, {\cdot} \,d{\bf s}\) is equal to something that looks like the path integral of the tangential component \({\bf F} ({\bf c} (t))\, {\cdot}\, {\bf T}(t)\) of \({\bf F}\) along \({\bf c}\). In fact, the last part of formula (1) is analogous to the path integral of a scalar function \(f\) along \({\bf c}\).footnote #
To compute a line integral in any particular case, we can either use the original definition or integrate the tangential component of \({\bf F}\) along \({\bf c}\), as prescribed by formula (1), whichever is easier or more appropriate.
example 1
Let \({\bf c}(t)= (\sin t, \cos t, t)\) with \(0 \leq t \leq 2\pi\). Let the vector field \({\bf F}\) be defined by \({\bf F}(x,y,z) = x{\bf i}+ y{\bf j}+ z{\bf k}\). Compute \(\int_{\bf c}{\bf F} \, {\cdot} \ d{\bf s}\).
solution Here, \({\bf F}({\bf c}(t)) \,{=}\, {\bf F}(\sin t,\cos t,t) \,{=}\, (\sin t){\bf i} \,{+}\, (\cos t){\bf j} \,{+}\, t{\bf k}\), and \({\bf c}'(t)\,{=} (\cos t){\bf i}- (\sin t){\bf j}+ {\bf k}\). Therefore, \[ {\bf F}({\bf c} (t))\, {\cdot}\, {\bf c}'(t) = \sin t \cos t -\cos t \sin t + t = t, \] and so \[ \int_{\bf c}{\bf F} \, {\cdot} \,d{\bf s} = \int^{2\pi}_0 t \,{\it dt} = 2\pi^2. \]
Another common way of writing line integrals is \[ \int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} = \int_{\bf c}F_1\,{\it dx} + F_2 \,{\it dy} + F_3 \,{\it dz}, \] where \(F_1, F_2\), and \(F_3\) are the components of the vector field \({\bf F}\). We call the expression \(F_1 \,{\it dx} + F_2 \,{\it dy} + F_3 \,{\it dz}\) a differential form.footnote # By definition, the integral of a differential form along a path \({\bf c}\), where \({\bf c}(t)=(x(t),y(t),z(t))\), is \[ \int_{\bf c}F_1 \,{\it dx} + F_2 \,{\it dy} + F_3 \,{\it dz}= \int^b_a\bigg(F_1 \frac{{\it dx}}{{\it dt}} + F_2 \frac{{\it dy}}{{\it dt}} +F_3 \frac{{\it dz}}{{\it dt}}\bigg) \,{\it dt} = \int_{\bf c} {\bf F} \, {\cdot} \,d{\bf s}. \]
Note that we may think of \(d {\bf s}\) as the differential form \(d {\bf s} = d x{\bf i} + {\it dy}{\bf j} + {\it dz}{\bf k}\). Thus, the differential form \(F_1 {\it dx} + F_2 {\it dy} + F_3 {\it dz}\) may be written as the dot product \({\bf F} \,{\cdot}\, d{\bf s}\).
361
example 2
Evaluate the line integral \[ \int_{\bf c} x^2 \,{\it dx} + {\it xy} \,{\it dy} + \,{\it dz}, \] where \({\bf c}\colon\, [0,1]\rightarrow {\mathbb R}^3\) is given by \({\bf c}(t) = (t,t^2, 1) = (x(t), y(t),z(t))\).
solution We compute \({\it dx}/{\it dt} = 1, \,{\it dy}/{\it dt} = 2t, \,{\it dz} /{\it dt} = 0 \); therefore, \begin{eqnarray*} \int_{\bf c}x^2 \,{\it dx} +{\it xy} \,{\it dy} + \,{\it dz} &=& \int^1_0\bigg([x(t)]^2\, \frac{{\it dx}}{{\it dt}} + [x(t)y(t)]\, \frac{{\it dy}}{{\it dt}} \bigg) \,{\it dt}\\[5pt] &=& \int_0^1 (t^2 + 2t^4) \,{\it dt} = \bigg[\frac{1}{3}t^3 + \frac{2}{5}t^5 \bigg]_0^1 = \frac{11}{15}.\\[-26pt] \end{eqnarray*}
Question 17.32 Section 17.2 Progress Check Question 1
Evaluate the line integral \[ \int_{\bf c} xz \,{\it dx} + {\it xy} \,{\it dy} + x^3z\,{\it dz}, \] where \({\bf c}\colon\, [1,2]\rightarrow {\mathbb R}^3\) is given by \({\bf c}(t) = (\frac{1}{t},t, t^3) = (x(t), y(t),z(t))\).
example 3
Evaluate the line integral \[ \int_{\bf c} \cos z \,{\it dx} \,+\, e^x \,{\it dy} \,+\, e^y \,{\it dz}, \] where the path \({\bf c}\) is defined by \({\bf c}(t) = (1,t,e^t)\) and \(0 \leq t \leq 2\).
solution We compute \({\it dx}/{\it dt} = 0,{\it dy}/{\it dt} = 1, \,{\it dz} /{\it dt} = e^t\), and so \begin{eqnarray*} \int_{\bf c}\cos z \,{\it dx} + e^x \,{\it dy} + e^y \,{\it dz} &=& \int^2_0(0 + e + e^{2t})\,{\it dt} \\[5pt] &=& \bigg[et + \frac{1}{2}e^{2t}\bigg]_0^2 = 2e + \frac{1}{2}e^4 - \frac{1}{2}.\\[-26pt] \end{eqnarray*}
example 4
Let \({\bf c}\) be the path \[ x = \cos^3 \theta, y = \sin^3 \theta, z =\theta, 0 \leq \theta \leq \frac{7 \pi}{2} \] (see Figure 17.7). Evaluate the integral \(\int_{\bf c}(\sin z \,{\it dx} + \cos z \,{\it dy} - ({\it xy})^{1/3}\,{\it dz})\).
solution In this case, we have \[ \frac{{\it dx}}{d\theta }= - 3 \cos^2 \theta \sin \theta, \qquad \frac{{\it dy}}{d \theta} = 3 \sin^2 \theta \cos \theta, \qquad \frac{{\it dz}}{d \theta} = 1, \] so the integral is \begin{eqnarray*} && \int_{\bf c}\sin z \,{\it dx} + \cos z \,{\it dy} - ({\it xy})^{1/3} \,{\it dz} \\[5pt] &&\quad = \int^{7\pi /2}_0 (-3 \cos^2 \theta \sin^2 \theta + 3 \sin^2 \theta \cos^2 \theta - \cos \theta \sin \theta)\,d\theta. \end{eqnarray*}
The first two terms cancel, and so we get \[ - \int^{7\pi /2}_0 \cos \theta \sin\, \theta\, d\theta ={-}\bigg[\frac{1}{2} \sin^2 \theta\bigg]_0^{7\pi /2} = -\frac{1}{2} . \]
362
example 5
Suppose \({\bf F}\) is the force vector field \({\bf F}(x,y,z)= x^3 {\bf i} + y{\bf j} + z{\bf k}\). Parametrize the circle of radius \(a\) in the \(yz\) plane by letting \({\bf c}(\theta)\) have components \[ x = 0,\qquad y = a \cos \theta,\qquad z = a \sin \theta, \qquad 0 \leq \theta \leq 2\pi . \]
Because \({\bf F}({\bf c}(\theta))\, {\cdot}\, {\bf c}' (\theta) = 0\), the force field \({\bf F}\) is normal to the circle at every point on the circle, so \({\bf F}\) will not do any work on a particle moving along the circle (Figure 17.8).
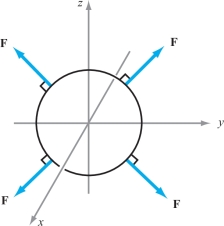
We can verify by direct computation that the work done by \({\bf F}\) is zero: \begin{eqnarray*} W &=& \int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} = \int_{\bf c} x^3 \,{\it dx} \, +\, y \,{\it dy} \, +\, z \,{\it dz} \\[4pt] &=& \int^{2\pi}_0 (0\, -\, a^2 \cos \theta \sin \theta\, +\, a^2 \cos \theta \ \sin \theta)\,d\theta =0.\\[-28pt] \end{eqnarray*}
363
example 6
If we consider the field and curve of Example 4, we see that the work done by the field is \(-\frac{1}{2}\), a negative quantity. This means that the field impedes movement along the path.
Question 17.33 Section 17.2 Progress Check Question 2
Let \({\bf F}\) be the force vector field \({\bf F}(x,y,z)= yz {\bf i} + xz{\bf j} + xy{\bf k}\) and let \({\bf c}\colon\, [0,2 \pi]\rightarrow (\cos t,\sin t, \cos t)\). Evaluate \(\int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s}\)
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
Reparametrizations
The line integral \(\int_{\bf c} {\bf F}\, {\cdot} \,d{\bf s}\) depends not only on the field \({\bf F}\) but also on the path \({\bf c}\colon\, [a,b] \rightarrow {\mathbb R}^3\). In general, if \({\bf c}_1\) and \({\bf c}_2\) are two different paths in \({\mathbb R}^3, \int_{{\bf c}_1}{\bf F}\, {\cdot}\, \,d{\bf s} \neq \int_{{\bf c}_2} {\bf F}\, {\cdot}\, \,d{\bf s}\). On the other hand, we shall see that it is true that \(\int_{{\bf c}_1}{\bf F}\, {\cdot} \,d{\bf s} = \pm \int_{{\bf c}_2} {\bf F}\, {\cdot}\,d{\bf s}\) for every vector field \({\bf F}\) if \({\bf c}_1\) is what we call a reparametrization of \({\bf c}_2\); roughly speaking, this means that \({\bf c}_1\) and \({\bf c}_2\) are different descriptions of the same geometric curve.
Definition
Let \(h\colon\, I \rightarrow I_1\) be a \(C^1\) real-valued function that is a one-to-one map of an interval \(I = [a,b]\) onto another interval \(I_1= [a_1,b_1]\). Let \({\bf c}\colon\, I_1\rightarrow {\mathbb R}^3\) be a piecewise \(C^1\) path. Then we call the composition \[ {\bf p} ={\bf c}\circ h\colon\, I \rightarrow {\mathbb R}^3 \] a reparametrization of \({\bf c}\).
This means that \({\bf p}(t) = {\bf c}(h(t))\), and so \(h\) changes the variable; alternatively, we can think of \(h\) as changing the speed at which a point moves along the path. Indeed, observe that \({\bf p}'(t) = {\bf c}'(h(t))h'(t)\), so that the velocity vector for \({\bf p}\) equals that for \({\bf c}\) but is multiplied by the scalar factor \(h'(t)\).
It is implicit in the definition that \(h\) must carry endpoints to endpoints; that is, either \(h(a) = a_1\) and \(h(b) = b_1\), or \(h(a) = b_1\) and \(h(b) = a_1\). We thus distinguish two types of reparametrizations. If \({\bf c}\circ h\) is a reparametrization of \({\bf c}\), then either \[ ({\bf c}\circ h)(a)= {\bf c}(a_1) \qquad\hbox{and}\qquad({\bf c}\circ h)(b)= {\bf c}(b_1) \] or \[ ({\bf c}\circ h)(a)= {\bf c}(b_1) \qquad\hbox{and}\qquad({\bf c}\circ h)(b)= {\bf c}(a_1). \]
In the first case, the reparametrization is said to be orientation-preserving, and a particle tracing the path \({\bf c}\circ h\) moves in the same direction as a particle tracing \({\bf c}\). In the second case, the reparametrization is described as orientation-reversing, and a particle tracing the path \({\bf c}\circ h\) moves in the opposite direction to that of a particle tracing \({\bf c}\) (Figure 17.9).
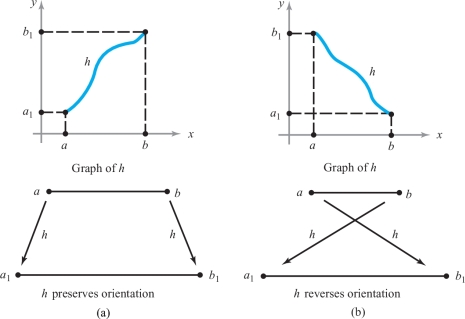
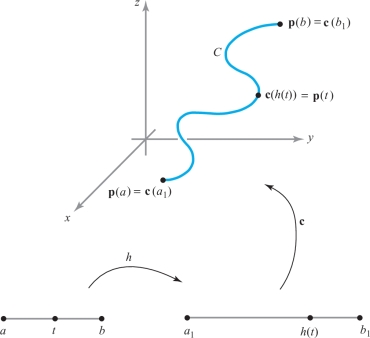
For example, if \(C\) is the image of a path \({\bf c}\), as shown in Figure 17.10—that is, \(C = {\bf c}([a_1,b_1]) \)—and if \(h\) is orientation-preserving, then \({\bf c}\circ h(t)\) will go from \({\bf c}(a_1)\) to \({\bf c}(b_1)\) as \(t\) goes from \(a\) to \(b \); and if \(h\) is orientation-reversing, \({\bf c}\circ h(t)\) will go from \({\bf c}(b_1)\) to \({\bf c}(a_1)\) as \(t\) goes from \(a\) to \(b\).
example 7
Let \({\bf c}\colon\, [a,b]\to {\mathbb R}^3\) be a piecewise \(C^1\) path. Then:
- (a) The path \({\bf c}_{\rm op}\colon\, [a,b]\to {\mathbb R}^3, t\mapsto {\bf c} (a+ b- t)\), is a reparametrization of \({\bf c}\) corresponding to the map \(h\colon\, [a,b]\to [a,b],t\mapsto a+b-t \); we call \({\bf c}_{\rm op}\) the opposite path to \({\bf c}\). This reparametrization is orientation-reversing.
- (b) The path \({\bf p}\colon\, [0,1]\to {\mathbb R}^3,t\mapsto {\bf c}(a+(b-a)t)\), is an orientation-preserving reparametrization of \({\bf c}\) corresponding to a change of coordinates \(h\colon\, [0,1]\to [a,b],t\mapsto a+(b-a)t\).
364
Theorem 1 Change of Parametrization for Line Integrals
Let \({\bf F}\) be a vector field continuous on the \(C^1\) path \({\bf c}\colon\, [a_1,b_1]\to {\mathbb R}^3\), and let \({\bf p}\colon\, [a,b]\to {\mathbb R}^3\) be a reparametrization of \({\bf c}\). If \({\bf p}\) is orientation-preserving, then \[ \int_{\bf p}{\bf F}\, {\cdot} \,d{\bf s} =\int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} , \] and if \({\bf p}\) is orientation-reversing, then \[ \int_{\bf p}{\bf F}\, {\cdot} \,d{\bf s} =-\int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} . \]
365
proof
By hypothesis, we have a map \(h\) such that \({\bf p}={\bf c}\circ h\). By the chain rule, \[ {\bf p}'(t)={\bf c}'(h(t))h'(t), \] and so \[ \int_{\bf p}{\bf F}\, {\cdot} \,d{\bf s} =\int^b_a[{\bf F}({\bf c}(h(t)))\, {\cdot}\, {\bf c}'(h(t))]h'(t)\,{\it dt} . \]
Changing variables with \(s=h(t)\), this becomes \begin{eqnarray*} &&\int^{h(b)}_{h(a)}{\bf F}({\bf c}(s))\, {\cdot}\, {\bf c}'(s)\,{\it ds} \\[5pt] &&\quad =\left\{ \begin{array}{l@{\qquad}l} \displaystyle\int_{a_1}^{b_1} {\bf F}({\bf c}(s)) {\, {\cdot}\, } {\bf c}'(s)\,{\it ds} = \int_{\bf c} {\bf F}{\, {\cdot}\, } \,d{\bf s} &\hbox{if \({\bf p}\) is orientation-}\\[-6pt] &\hbox{preserving}\\ \displaystyle\int_{b_1}^{a_1} {\bf F} ({\bf c}(s)) {\, {\cdot}\, } {\bf c}'(s)\,{\it ds} = -\int_{\bf c} {\bf F}{\, {\cdot}\, } \,d{\bf s} &\hbox{if }{\bf p} \hbox{ is orientation-}\\[-6pt] & \hbox{reversing.} \end{array}\right. \\[-28pt] \end{eqnarray*}
Theorem 1 also holds for piecewise \(C^1\) paths, as may be seen by breaking up the intervals into segments on which the paths are of class \(C^1\) and summing the integrals over the separate intervals.
Thus, if it is convenient to reparametrize a path when evaluating an integral, Theorem 1 assures us that the value of the integral will not be affected, except possibly for the sign, depending on the orientation.
example 8
Let \({\bf F}(x,y,z)=yz{\bf i}+xz{\bf j}+{\it xy}{\bf k}\) and \({\bf c} \colon\, [-5,10]\to {\mathbb R}^3\) be defined by \(t\mapsto (t,t^2,t^3)\). Evaluate \(\int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s}\) and \(\int_{{\bf c}_{\rm op}}{\bf F}\, {\cdot} \,d{\bf s}\).
solution For the path \({\bf c}\), we have \({\it dx}/{\it dt}\,{=}\,1, \,{\it dy} /{\it dt}\,{=}\,2t, \,{\it dz} /{\it dt}\,{=}\,3t^2\), and \({\bf F} ({\bf c}(t))= t^5{\bf i}+t^4{\bf j}+t^3{\bf k}\). Therefore, \begin{eqnarray*} \int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} &=& \int^{10}_{-5} \bigg(F_1\frac{{\it dx}}{{\it dt}}+F_2\frac{{\it dy}}{{\it dt}}+F_3\frac{{\it dz}}{{\it dt}}\bigg)\,{\it dt} \\[6pt] &=& \int^{10}_{-5}(t^5+2t^5+3t^5)\,{\it dt} =[t^6]^{10}_{-5}= \hbox{984,375}. \end{eqnarray*}
On the other hand, for \[ {\bf c}_{\rm op}\colon\,[-5,10]\to {\mathbb R}^3,t\mapsto {\bf c}(5-t) =(5-t,(5-t)^2,(5-t)^3), \] we have \({\it dx}/{\it dt}=-1, \,{\it dy} /{\it dt}=-10+2t=-2(5-t), \,{\it dz} /{\it dt}=-75 + 30t-3t^2= -3(5-t)^2\), and \({\bf F}({\bf c}_{\rm op}(t))=(5-t)^5{\bf i}+(5-t)^4 {\bf j}+(5-t)^3{\bf k}\). Therefore, \[ \int_{{\bf c}_{\rm op}}{\bf F}\, {\cdot} \,d{\bf s} = \int^{10}_{-5} [-(5-t)^5-2(5-t)^5-3(5-t)^5]\,{\it dt} = [(5-t)^6]^{10}_{-5}=-984,375. \]
We are interested in reparametrizations, because if the image of a particular \({\bf c}\) can be represented in many ways, we want to be sure that path and line integrals depend only on the image curve and not on the particular parametrization. For example, for some problems the unit circle may be conveniently represented by the map \({\bf p}\) given by \[ x(t)=\cos 2t, \qquad y(t)=\sin 2t,\qquad 0\leq t\leq \pi. \]
366
Theorem 1 guarantees that any integral computed for this representation will be the same as when we represent the circle by the map \({\bf c}\) given by \[ x(t)=\cos t,\qquad y(t)=\sin t,\qquad 0\leq t\leq 2\pi, \] because \({\bf p}= {\bf c} \,\circ\, h\), where \(h(t) = 2t\), and thus \({\bf p}\) is an orientation-preserving reparametrization of \({\bf c}\). However, notice that the map \(\gamma\) given by \[ \gamma(t)=(\cos t,\sin t),\qquad 0\leq t\leq 4\pi \] is not a reparametrization of \({\bf c}\). Although it traces out the same image (the circle), it does so twice. (Why does this imply that \(\gamma\) is not a reparametrization of \({\bf c}\)?)
The line integral is an oriented integral, in that a change of sign occurs (as we have seen in Theorem 1) if the orientation of the curve is reversed. The path integral does not have this property. This follows from the fact that changing \(t\) to \(-t\) (reversing orientation) just changes the sign of \({\bf c}'(t)\), not its length. This is one of the differences between line and path integrals. The following theorem, which is proved by the same method as in Theorem 1, shows that path integrals are unchanged under reparametrizations—even orientation-reversing ones.
Theorem 2 Change of Parametrization for Path Integrals
Let \({\bf c}\) be piecewise \(C^1\), let \(f\) be a continuous (real-valued) function on the image of \({\bf c}\), and let \({\bf p}\) be any reparametrization of \({\bf c}\). Then \begin{equation} \int_{\bf c}f(x,y,z)\,{\it ds} =\int_{\bf p} f(x,y,z)\,{\it ds} . \end{equation}
Line Integrals of Gradient Fields
We next consider a useful technique for evaluating certain types of line integrals. Recall that a vector field \({\bf F}\) is a gradient vector field if \({\bf F}=\nabla\! f\) for some real-valued function \(f\). Thus, \[ {\bf F}=\frac{\partial f}{\partial x}\,{\bf i}+ \frac{\partial f}{\partial y}\,{\bf j}+ \frac{\partial f}{\partial z}\,{\bf k} . \]
Suppose \(g\) and \(G\) are real-valued continuous functions defined on a closed interval \([a, b]\), that \(G\) is differentiable on \((a,b)\), and that \(G'=g\). Then by the fundamental theorem of calculus \[ \int_a^b g(x)\,{\it dx} =G(b)-G(a). \]
Thus, the value of the integral of \(g\) depends only on the value of \(G\) at the endpoints of the interval \([a, b]\). Because \(\nabla\! f\) represents the derivative of \(f\), we can ask whether \(\int_{\bf c} \nabla\! f \, {\cdot} \,d{\bf s}\) is completely determined by the value of \(f\) at the endpoints \({\bf c}(a)\) and \({\bf c}(b)\). The answer is contained in the following generalization of the fundamental theorem of calculus.
367
Theorem 3 Line Integrals of Gradient Vector Fields
Suppose \(f\colon \,{\mathbb R}^3\,{\to}\,{\mathbb R}\) is of class \(C^1\) and that \({\bf c}\colon\,[a,b]\to {\mathbb R}^3\) is a piecewise \(C^1\) path. Then \[ \int_{\bf c}\nabla\! f\, {\cdot} \,d{\bf s} =f({\bf c}(b))- f({\bf c}(a)). \]
proof
Apply the chain rule to the composite function \[ F\colon\, t\mapsto f({\bf c}(t)) \] to obtain \[ F'(t)=(f\circ {\bf c})'(t)=\nabla\! f({\bf c}(t))\, {\cdot}\, {\bf c}'(t). \]
The function \(F\) is a real-valued function of the variable \(t\), and so, by the fundamental theorem of single-variable calculus, \[ \int^b_a F'(t)\,{\it dt} =F(b)-F(a)=f({\bf c}(b))-f({\bf c}(a)). \]
Therefore, \begin{eqnarray*} \int_{\bf c}\nabla\! f \, {\cdot} \,d{\bf s} =\int^b_a\nabla\! f({\bf c} (t)) \, {\cdot} \, {\bf c}' (t) \,{\it dt} &=&\int^b_a F'(t) \,{\it dt} =F(b) -F(a)\\[4pt] &=&f({\bf c}(b))-f({\bf c}(a)). \\[-35pt] \end{eqnarray*}
example 9
Let \({\bf c}\) be the path \({\bf c}(t)=(t^4/4,\sin^3(t\pi /2),0), t \in [0,1]\). Evaluate \[ \int_{\bf c}y \,{\it dx} +x \,{\it dy} \] \(\big(\)which means \(\int_{\bf c}y \,{\it dx} +x \,{\it dy} +0 \,{\it dz}\big)\).
solution We recognize \(y \,{\it dx} +x \,{\it dy}\), or, equivalently, the vector field \(y{\bf i}+x{\bf j}+0 {\bf k}\), as the gradient of the function \(f(x,y,z)={\it xy}\). Thus, \[ \int_{\bf c}y \,{\it dx} +x \,{\it dy} =f({\bf c}(1)) -f({\bf c}(0))= \frac{1}{4}\, {\cdot}\, 1-0=\frac{1}{4}. \]
Obviously, if we can recognize the integrand as a gradient, then evaluation of the integral becomes much easier. For example, try to work out the integral in Example 9 directly. In one-variable calculus, every integral is, in principle, obtainable by finding an antiderivative. For vector fields, however, this is not always true, because a given vector field need not be a gradient. This point will be examined in detail in Section 18.3, where we derive a test to determine when a vector field \({\bf F}\) is a gradient; that is, when \({\bf F} = \nabla f\) for some \(f\).
Question 17.34 Section 17.2 Progress Check Question 3
Let \({\bf F}\) be the force vector field \({\bf F}(x,y,z)= yz {\bf i} + xz{\bf j} + xy{\bf k}\) and let \({\bf c}\colon\, [0,2 \pi]\rightarrow (\cos t,\sin t, \cos t)\). Evaluate \(\int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s}\)
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
Line Integrals Over Geometric Curves
368
We have seen how to define path integrals (integrals of scalar functions) and line integrals (integrals of vector functions) over parametrized curves. We have also seen that our work is simplified if we make a judicious choice of parametrization. Because these integrals are independent of the parametrization (except possibly for the sign), it seems natural to express the theory in a way that is independent of the parametrization, and that is thereby more “geometric.” We do this briefly and somewhat informally in the following discussion.
Definition
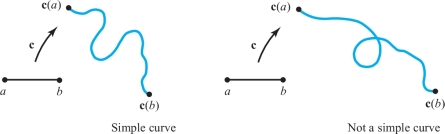
We define a simple curve \(C\) to be the image of a piecewise \(C^1\) map \({\bf c}\colon\, I\to {\mathbb R}^3\) that is one-to-one on an interval \(I;{\bf c}\) is called a parametrization of \(C\). Thus, a simple curve is one that does not intersect itself (Figure 17.11). If \(I = [a,b]\), we call \({\bf c}(a)\) and \({\bf c}(b)\) endpoints of the curve.
Each simple curve \(C\) has two orientations or directions associated with it. If P and Q are the endpoints of the curve, then we can consider \(C\) as directed either from P to Q or from Q to P. The simple curve \(C\) together with a sense of direction is called an oriented simple curve or directed simple curve (Figure 17.12).

Definition: Simple Closed Curves
By a simple closed curve we mean the image of a piecewise \(C^1\) map \({\bf c}\colon\, [a,b]\to {\mathbb R}^3\) that is one-to-one on \([a, b)\) and satisfies \({\bf c}(a)={\bf c}(b)\) (Figure 17.13). If \({\bf c}\) satisfies the condition \({\bf c}(a)={\bf c}(b)\), but is not necessarily one-to-one on \([a, b)\), we call its image a closed curve. Simple closed curves have two orientations, corresponding to the two possible directions of motion along the curve (Figure 17.14).
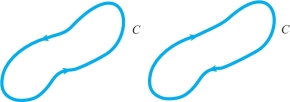
If \(C\) is an oriented simple curve or an oriented simple closed curve, we can unambiguously define line integrals along them.
369
Line Integrals and Path Integrals Over Oriented Simple Curves and Simple Closed Curves \(C\):
\begin{equation} \int_C{\bf F}\, {\cdot} \,d{\bf s} =\int_{\bf c}{\bf F}{\, {\cdot}\, } \,d{\bf s} \qquad \hbox{ and }\qquad \int_C fd s=\int_{\bf c}f \,{\it ds} , \end{equation} where \({\bf c}\) is any orientation-preserving parametrization of \(C\).
These integrals do not depend on the choice of \({\bf c}\) as long as \({\bf c}\) is one-to-one (except possibly at the endpoints) by virtue of Theorems 1 and 2.footnote # The point we want to make here is that, although a curve must be parametrized to make integration along it tractable, it is not necessary to include the parametrization in our notation for the integral.
example 10
If \(I=[a,b]\) is a closed interval on the \(x\) axis, then \(I\), as a curve, has two orientations: one corresponding to motion from \(a\) to \(b\) (left to right) and the other corresponding to motion from \(b\) to \(a\) (right to left). If \(f\) is a real-valued function continuous on \(I\), then denoting \(I\) with the first orientation by \(I^+\) and \(I\) with the second orientation by \(I^-\), we have \[ \int_{I^+}f(x)\,{\it dx} =\int^b_af(x)\,{\it dx} =-\int^a_b f(x) \,{\it dx}=-\int_{I^-}f(x)\,{\it dx} . \]
A given simple closed curve can be parametrized in many different ways. Figure 17.15 shows \(C\) represented as the image of a map \({\bf p}\), with \({\bf p}(t)\) progressing in a prescribed direction around an oriented curve \(C\) as \(t\) ranges from \(a\) to \(b\). Note that \({\bf p}'(t)\) points in this direction also. The speed with which we traverse \(C\) may vary from parametrization to parametrization, but as long as the orientation is preserved, the integral will not, according to Theorems 1 and 2.
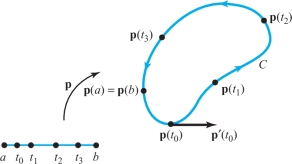
The following precaution should be noted in regard to these remarks. It is possible to have two mappings \({\bf c}\) and \({\bf p}\) with the same image, and inducing the same orientation on the image, such that \[ \int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} \neq \int_{\bf p} {\bf F}\, {\cdot} \,d{\bf s} . \]
370
For an example, let \({\bf c}(t)=(\cos t,\sin t,0)\) and \({\bf p} (t) =(\cos 2t,\sin 2t ,0),0\leq t\leq 2\pi\), with \({\bf F}(x,y,z)\,{=}\,(y,0,0)\). Then \(F_1 (x,y,z)\,{=}\,y, F_2 (x,y,z)\,{=}\,0\), and \(F_3 (x,y,z)\,{=}\,0\), so \[ \int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} =\int^{2\pi}_{0} F_1({\bf c}(t))\,\frac{{\it dx}}{{\it dt}}\,{\it dt} \ =-\int^{2\pi}_{0}\sin^2 t \,{\it dt} =-\pi. \]
But \(\int_{\bf p}{\bf F}\, {\cdot} \,d{\bf s} =-2\int^{2\pi}_{0} \sin^2 2t \,{\it dt} =-2\pi\). Clearly, \({\bf c}\) and \({\bf p}\) have the same image, namely, the unit circle in the \({\it xy}\) plane. Moreover, they traverse the unit circle in the same direction; yet \(\int_{\bf c}{\bf F}\, {\cdot} \,d{\bf s} \neq \int_{\bf p}{\bf F}\, {\cdot} \,d{\bf s}\). The reason for this is that \({\bf c}\) is one-to-one, but \({\bf p}\) is not (\({\bf p}\) traverses the unit circle twice in a counterclockwise direction); therefore, \({\bf p}\) is not a parametrization of the unit circle as a simple closed curve.
As a consequence of Theorem 1 and generalizing the notation in Example 10, we introduce the following convention:
Line Integrals Over Curves with Opposite Orientations
Let \(C^-\) be the same curve as \(C\), but with the opposite orientation. Then \[ \int_C {\bf F}\, {\cdot} \,d{\bf s} = - \int_{C^-}{\bf F}\, {\cdot} \,d{\bf s}. \]
We also have:
Line Integrals Over Curves Consisting of Several Components
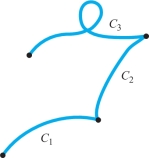
Let \(C\) be an oriented curve that is made up of several oriented component curves \(C_i,i=1, \ldots , k\), as in Figure 17.16. Then we shall write \(C=C_1+C_2+ \cdots + C_k\). Because we can parametrize \(C\) by parametrizing the pieces \(C_1,\ldots ,C_k\) separately, we can prove that \begin{equation} \int_C{\bf F}\, {\cdot} \,d{\bf s} =\int_{C_1}{\bf F}\, {\cdot} \,d{\bf s} +\int_{C_2}{\bf F}\, {\cdot} \,d{\bf s} +\cdots +\int_{C_k}{\bf F}{\, {\cdot}\,} \,d{\bf s} . \end{equation}
One reason for writing a curve as a sum of components is that it may be easier to parametrize the components \(C_i\) individually than it is to parametrize \(C\) as a whole. If that is the case, formula (4) provides a convenient way of evaluating \(\int_C {\bf F}{\,{\cdot}\,}\, d{\bf s}\).
The r Notation for Line Integrals
371
Sometimes one writes, as we occasionally do later, the line integral using the notation \[ \int _{C} {\bf F} \,{\cdot}\, d{\bf r.} \]
The reason is that we think of describing a \(C^{1}\) path \({\bf c}\) in terms of a moving position vector based at the origin and ending at the point \({\bf c}(t)\) at time \(t\). Position vectors are often denoted by \({\bf r} = x{\bf i} + y{\bf j} + z{\bf k}\), and so the curve is described using the notation \({\bf r}(t)\,{=}\,x(t){\bf i} \,{+}\, y(t){\bf j} \,{+}\, z(t){\bf k}\) in place of \({\bf c}(t)\). By definition, the line integral is given by \[ \int_a^b {\bf F}({\bf r}(t)) \,{\cdot}\, \frac{d{\bf r}}{{\it dt}}\, {\it dt}. \]
Formally canceling thedt’s, and using the parametrization independence to replace the limits of integration with the geometric curve \(C\), we arrive at the notation \(\int _{C} {\bf F}\,{\cdot}\, d{\bf r}\).
example 11
Consider \(C\), the perimeter of the unit square in \({\mathbb R}^2\), oriented in the counterclockwise sense (see Figure 17.17). Evaluate the line integral \[ \int_C x^2 \,{\it dx} + {\it xy} \,{\it dy} . \]
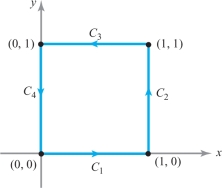
solution We evaluate the integral using a convenient parametrization of \(C\) that induces the given orientation. For example: \[ {\bf c}\colon\, [0,4]\to {\mathbb R}^2,\qquad t\mapsto \left \{\begin{array}{l@{\qquad}c} (t,0) & 0\leq t\leq 1\\[.5pt] (1,t-1) & 1\leq t\leq 2\\[.5pt] (3-t,1) & 2\leq t\leq 3\\[.5pt] (0,4-t) & 3\leq t\leq 4. \end{array}\right. \]
Then \begin{eqnarray*} \int_C x^2 \,{\it dx} +{\it xy} \,{\it dy} &=&\int^1_0(t^2+0)\,{\it dt} +\int^2_1[0+(t-1)]\,{\it dt} \\[5pt] &&+\int^3_2[-(3-t)^2+0]\,{\it dt} +\int^4_3 (0+0)\,{\it dt} \\[5pt] &=& \frac{1}{3}+ \frac{1}{2} + \bigg(\!{-}\frac{1}{3}\bigg)+0= \frac{1}{2}.\\[-30pt] \end{eqnarray*}
372
Now let us reevaluate this line integral, using formula (4) and parametrizing the \(C_i\) separately. Notice that \(C = C_1 + C_2 + C_3 + C_4\), where \(C_i\) are the oriented curves pictured in Figure 17.17. These can be parametrized as follows: \begin{eqnarray*} && C_1\colon\, \,{\bf c}_1(t)=(t,0),0 \leq t\leq 1\\ && C_2\colon\, \,{\bf c}_2(t)=(1,t),0 \leq t\leq 1\\ && C_3\colon\, \,{\bf c}_3(t)=(1-t,1),0 \leq t\leq 1\\ && C_4\colon\, \,{\bf c}_4(t)=(0,1-t),0 \leq t\leq 1, \end{eqnarray*} and so \begin{eqnarray*} && \int_{C_1} x^2 \,{\it dx} +{\it xy} \,{\it dy} = \int^1_0 t^2 \,{\it dt} =\frac{1}{3}\\[5pt] && \int_{C_2} x^2 \,{\it dx} +{\it xy} \,{\it dy} = \int^1_0 t \,{\it dt} =\frac{1}{2}\\[5pt] && \int_{C_3} x^2 \,{\it dx} +{\it xy} \,{\it dy} = \int^1_0 -(1-t)^2 \,{\it dt} = - \frac{1}{3}\\[5pt] && \int_{C_4} x^2 \,{\it dx} +{\it xy} \,{\it dy} = \int^1_0 0 \,{\it dt} =0. \end{eqnarray*}
Thus, again, \[ \int_C x^2 \,{\it dx} +{\it xy} \,{\it dy} =\frac{1}{3}+\frac{1}{2}-\frac{1}{3}+0= \frac{1}{2}. \]
Question 17.35 Section 17.2 Progress Check Question 4
Let \({\bf F}\) be the vector field \({\bf F}(x,y,z)= -y {\bf i} + x {\bf j} + \pi \sin (\pi z){\bf k}\) and let the curve \({C}\) be the perimeter of the triangle with vertices \((1,0,0), (0,1,0)\) and \((0,0,1)\), in that order. Evaluate
\[ \int _{C} {\bf F} \,{\cdot}\, d{\bf r.} \]
| A. |
| B. |
| C. |
| D. |
| E. |
| F. |
example 12
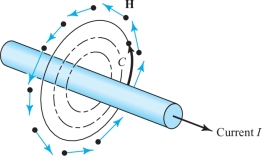
An interesting application of the line integral is the mathematical formulation of Ampère’s law, which relates electric currents to their magnetic effects.footnote # Suppose \({\bf H}\) denotes a magnetic field in \({\mathbb R}^3\), and let \(C\) be a closed oriented curve in \({\mathbb R}^3\). In appropriate physical units, Ampère’s law states that \[ \int_C {\bf H}\, {\cdot}\, d {\bf s}=I, \] where \(I\) is the net current that passes through any surface bounded by \(C\) (see Figure 17.18).
373
Finally, let us mention that the line integral has another important physical meaning, specifically, the interpretation of \(\int_C {\bf V}\, {\cdot} \,d{\bf s}\) as circulation, where \({\bf V}\) is the velocity field of a fluid, as we shall discuss in Section 18.2. Thus, a wide variety of physical concepts, from the notion of work to electromagnetic fields and the motions of fluids, can be analyzed with the help of line integrals.