17.3 Parametrized Surfaces
In Section 17.1 and Section 17.2, we studied integrals of scalar and vector functions along curves. Now we turn to integrals over surfaces and begin by studying the geometry of surfaces themselves.
Graphs Are Too Restrictive
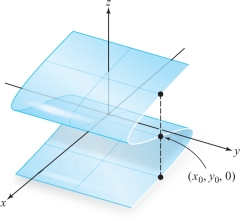
We are already used to one kind of surface, namely, the graph of a function \(f(x, y)\). Graphs were extensively studied in Chapter 13, and we know how to compute their tangent planes. However, it would be unduly limiting to restrict ourselves to this case. For example, many surfaces arise as level surfaces of functions. Suppose our surface \(S\) is the set of points \((x, y, z)\), where \(x-z+z^3=0\). Here \(S\) is a sheet that (relative to the \({\it xy}\) plane) doubles back on itself (see Figure 17.22). Obviously, we want to call \(S\) a surface, because it is just a plane with a wrinkle. However, \(S\) is not the graph of some function \(z = f(x, y)\), because this means that for each \((x_0,y_0)\in {\mathbb R}^2\) there must be one \(z_0\) with \((x_0,y_0,z_0)\in S\). As Figure 17.22 illustrates, this condition is violated.
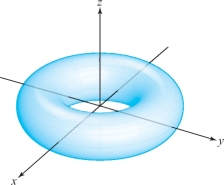
Another example is the torus, or surface of a doughnut, which is depicted in Figure 17.23. Anyone would call a torus a surface; yet, by the same reasoning as before, a torus cannot be the graph of a differentiable function of two variables. These observations encourage us to extend our definition of a surface.
376
The motivation for the extended definition that follows is partly that a surface can be thought of as being obtained from the plane by “rolling,” “bending,” and “pushing.” For example, to get a torus, we take a portion of the plane and roll it (see Figure 17.24), then take the two “ends” and bring them together until they meet (Figure 17.25).
Parametrized Surfaces as Mappings
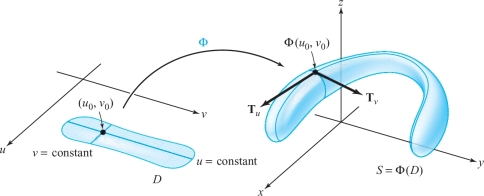
In our study of differential calculus we dealt with mappings \(f{:}\,A\subset {\mathbb R}^{n}\to {\mathbb R}^m\). Taking \({n=2}\) and \({m=3}\) corresponds to the case of a two-dimensional surface in 3-space. With surfaces, just as with curves, we want to distinguish a map (a parametrization) from its image (a geometric object). This leads us to the following definition.
377
Definition: Parametrized Surfaces
A parametrization of a surface is a function \({\Phi} \colon\, D\subset {\mathbb R}^2\to {\mathbb R}^3\), where \(D\) is some domain in \({\mathbb R}^2\). The surface \(S\) corresponding to the function \({\Phi}\) is its image: \(S={\Phi}(D)\). We can write \[ {\Phi}(u,v)=(x(u,v),y(u,v),z(u,v)). \]
If \({\Phi}\) is differentiable or is of class \(C^1\) [which is the same as saying that \(x(u, v), y(u, v)\), and \(z(u, v)\) are differentiable or \(C^1\) functions of \((u, v) \)], we call \(S\) a differentiable or a \(C^1\) surface.
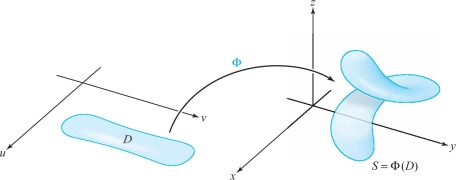
We can think of \({\Phi}\) as twisting or bending the region \(D\) in the plane to yield the surface \(S\) (see Figure 17.26). Thus, each point \((u, v)\) in \(D\) becomes a label for a point \((x(u, v), y(u, v), z(u, v))\) on \(S\).
Of course, surfaces need not bend or twist at all. In fact, planes are flat, as shown in our first, and simplest, example.
example 1
In Section 11.3 we studied the equation of a plane \(P\). We did so in terms of graphs and level sets. Now we examine the same notion using a parametrization.
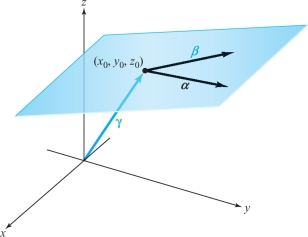
Let \(P\) be a plane that is parallel to two vectors \({\alpha}\) and \({\beta}\) and that passes through the tip of another vector \({\gamma}\), as in Figure 17.27.
378
Our goal in this example is to find a parametrization of this plane. Notice that the vector \({\alpha}\times {\beta} = {\bf N}\), which we also write as \(A{\bf i} + B{\bf j} + C{\bf k}\), is normal to \(P\). If the tip of \({\gamma}\) is the point (\(x_{0}\), \(y_{0}\), \(z_{0})\), then the equation of \(P\) as a level set (as discussed in Section 11.3) is given by: \[ A(x- x_{0})+B(y- y_{0})+C(z - z_{0}) = 0. \]
However, the set of all points on the plane \(P\) can also be described by the set of all vectors that are \({\gamma}\) plus a linear combination of \({\alpha}\) and \({\beta}\). Using our preferred choice of real parameters \(u\) and \(v\), we arrive at the parametric equation of the planeP: \[ {\Phi} (u, v) = {\alpha}u + {\beta}v + {\gamma.} \]
Tangent Vectors to Parametrized Surfaces
Suppose that \({\Phi}\) is a parametrized surface that is differentiable at \((u_0,v_0)\in {\mathbb R}^2\). Fixing \(u\) at \(u_0\), we get a map \({\mathbb R}\to {\mathbb R}^3\) given by \(t\mapsto {\Phi}(u_0,t)\), whose image is a curve on the surface (Figure 17.28). From Chapters 2 and 4 we know that the vector tangent to this curve at the point \({\Phi}(u_0,v_0)\), which we denote by \({\bf T}_v\), is given by \[ {\bf T}_v=\frac{\partial {\Phi}}{\partial v}=\frac{\partial x}{\partial v}(u_0,v_0){\bf i}+ \frac{\partial y}{\partial v}(u_0,v_0){\bf j}+ \frac{\partial z}{\partial v}(u_0,v_0){\bf k}. \]
Similarly, if we fix \(v\) and consider the curve \(t\mapsto {\Phi}(t,v_0)\), we obtain the tangent vector to this curve at \({\Phi}(u_0,v_0)\), given by \[ {\bf T}_u=\frac{\partial {\Phi}}{\partial u} =\frac{\partial x}{\partial u}(u_0,v_0){\bf i}+ \frac{\partial y}{\partial u}(u_0,v_0){\bf j}+ \frac{\partial z}{\partial u}(u_0,v_0){\bf k}. \]
Regular Surfaces
Because the vectors \({\bf T}_{u}\) and \({\bf T}_{v}\) are tangent to two curves on the surface at a given point, the vector \({\bf T}_{u}\,{\times}\,{\bf T}_{v}\) ought to be normal to the surface at the same point.
We say that the surface \(S\) is regular or smoothfootnote # at \({\Phi} (u_{0}\), \(v_{0})\), provided that \({\bf T}_{u}\,\times {\bf T}_{v} \ne {0}\) at (\(u_{0}\), \(v_{0})\). The surface is called regular if it is regular at all points \({\Phi} (u_{0}\), \(v_{0}) \in S\). The nonzero vector \({\bf T}_{u} \times {\bf T}_{v}\) is normal to \(S\) (recall that the vector product of \({\bf T}_{u}\) and \({\bf T}_{v}\) is perpendicular to the plane spanned by \({\bf T}_{u}\) and \({\bf T}_{v})\); the fact that it is nonzero ensures that there will be a tangent plane. Intuitively, a smooth surface has no “corners.”footnote #
379
example 2
Consider the surface given by the equations \[ x=u \cos v,\qquad y=u \sin v,\qquad z=u,\qquad u \ge 0. \]
Is this surface differentiable? Is it regular?
solution These equations describe the surface \(z=\sqrt{x^2+y^2}\) (square the equations for \(x, y\), and \(z\) to check this), which is shown in Figure 17.29. This surface is a cone with a “point” at \((0, 0, 0) \); it is a differentiable surface because each component function is differentiable as a function of \(u\) and \(v\). However, the surface is not regular at \((0, 0, 0)\). To see this, compute \({\bf T}_u\) and \({\bf T}_v\) at \((0, 0)\in {\mathbb R}^2 \): \[ {\bf T}_u =\frac{\partial {\Phi}}{\partial u} = \frac{\partial x}{\partial u}(0,0){\bf i}+ \frac{\partial y}{\partial u}(0,0){\bf j}+\frac{\partial z}{\partial u}(0,0){\bf k} =(\cos 0){\bf i}+(\sin 0){\bf j}+{\bf k}={\bf i}+{\bf k}, \] and similarly, \[ {\bf T}_v =\frac{\partial {\Phi}}{\partial v} = 0({-}\sin 0){\bf i}+0(\cos 0){\bf j}+0{\bf k}={\bf 0}. \] Thus, \({\bf T}_u\times {\bf T}_v={\bf 0}\), and so, by definition, the surface is not regular at \((0, 0, 0)\).
Question 17.58 Section 17.3 Progress Check Question #1
Z8SjSpiXpO68PEr6NRyfJy72hs4am5xqSZLJgP/+/rrNKbX0kD85eOECna0BG7L/oG8/YMw6AUFNHqfGwdDBdLzeY2P+IHFmFke/hug0LwCfesQNgGV4kShL+5O3m1VU/q26tTn19jzVfyRPrslKfP/rwswy+wXTTvEpxAX9lEgGyCKk6VCyzIxidsVfk0q4DH2/0aE+39HN28ZfeBPXv4OfoJxjco9fFqhO6yEXzvOLqfUfB2tHYotfB5g5ON7DqNeieMuxV6c1yFhAs5OWsMQia8SGACr0G02ADySowK6D7SHuVJV8OMn+j+/U001JBaWNQx43/VSsW1TrBxD7/l1NqLCIEA7zI44cJhUZhy3QK83ifMPBklQz9OcAVLfHpkxFjI7yjBCcFBgAwj3LWDZaRwOnnK0P78KBrbLnStymFjR9B3FlxknU3Xx1XdGh114lfp/dP+dQSjWoAMzvIzoo9Uv47QgHBW224gCj2JQ261dpea/F/jd4wZ1KleubCxwcaxXNnwXckKF6U+8dVa4vvAvL2wzKzB7LvjMua94+m7up5OcMqIVXbxnlfIwNvhOvY2bndog=Tangent Plane to a Parametrized Surface
We can use the fact that \({{\bf n}={\bf T}_u\,{\times}\,{\bf T}_v}\) is normal to the surface to both formally define the tangent plane and to compute it.
Definition: The Tangent Plane to a Surface
If a parametrized surface \({\Phi}\colon\, D\subset {\mathbb R}^2\to {\mathbb R}^3\) is regular at \({\Phi}(u_0,v_0) \)—that is, if \({\bf T}_u\times {\bf T}_v\neq {\bf 0}\) at \((u_0,v_0)\)—we define the tangent plane of the surface at \({\Phi}(u_0,v_0)\) to be the plane determined by the vectors \({\bf T}_u\) and \({\bf T}_v\). Thus, \({\bf n} = {\bf T}_u \times {\bf T}_v\) is a normal vector, and an equation of the tangent plane at \((x_0, y_0, z_0)\) on the surface is given by \begin{equation*} (x-x_0,y-y_0,z-z_0)\, {\cdot}\, {\bf n}=0,\tag{1} \end{equation*} where \({\bf n}\) is evaluated at \((u_0,v_0) \); that is, the tangent plane is the set of \((x,y,z)\) satisfying (1). If \({\bf n}=(n_1,n_2,n_3)= n_1{\bf i}+n_2{\bf j}+n_3{\bf k}\), then formula (1) becomes \begin{equation*} n_1(x-x_0)+n_2(y-y_0)+n_3(z-z_0)=0.\tag{1'} \end{equation*}
380
example 3
Let \({\Phi}\colon\, {\mathbb R}^2\to {\mathbb R}^3\) be given by \[ x = u \cos v,\qquad y = u \sin v,\qquad z = u^2 + v^2. \]
Where does a tangent plane exist? Find the tangent plane at \({\Phi}(1, 0)\).
solution We compute \[ {\bf T}_u = (\cos v){\bf i}+(\sin v){\bf j}+2u{\bf k} \qquad \hbox{and} \qquad {\bf T}_v = -u(\sin v){\bf i}+u(\cos v){\bf j}+2v{\bf k}, \] so the tangent plane at the point \({\Phi}(u_0,v_0)\) is the set of vectors through \({\Phi}(u_0,v_0)\) perpendicular to \[ ({\bf T}_u\times {\bf T}_v) (u_0, v_0)=\big({-}2u_0^2\cos v_0+2v_0 \sin v_0,-2u_0^2 \sin v_0-2v_0 \cos v_0, u_0\big) \] if this vector is nonzero. Because \({\bf T}_u\times {\bf T}_v\) is equal to \({\bf 0}\) at \((u_0, v_0) = (0,0)\), we cannot find a tangent plane at \({\Phi}(0,0)=(0,0,0)\). However, we can find an equation of the tangent plane at all the other points, where \({\bf T}_u\,{\times}\, {\bf T}_v\,{\neq}\, {\bf 0}\). At the point \({\Phi}(1,0)\,{=}\,(1,0,1)\), \[ {\bf n}= ({\bf T}_u\times {\bf T}_v) (1, 0)=(-2,0,1) = - 2{\bf i}+{\bf k}. \]
Because we have the vector \({\bf n}\) normal to the surface and a point \((1, 0, 1)\) on the surface, we can use formula \((1')\) to obtain an equation of the tangent plane: \[ -2(x-1)+ (z-1)=0; \hbox{ that is, } z=2x-1. \]
Question 17.59 Section 17.3 Progress Check Question #2
hNZpPZEieBF1FnCTq44V25pJMXC9x4HIQeYm8WfAzlGXUu/4iJI6Xy5FnSqawDPbx774XJJCLFkCCxFUT0I4LcMRezz8I4Tm4AlbeTBUKvqxmTTGYFy4JVuGVetyrszCeWqTDXCBqlZs8O9hwdvJ7i6C3oMpLb21I3PAdI1jqaTO/ZDqiRFXrX+8wP60y66oOQBQj27MPc26/2WMgOOllI3mCTTShuECCoCLL2I+kqRe07pvYCqs+uS2HhldRxvbeXxTXxTA8aiFUXJ0tLlKY8xOsui5xZnHNqXdv0sFpqR40oJU/ojLtiTfR8tUwM9LVloHiAnE5uSEM2BRG1qbQy1/lbOorD0jXLCWOh0Urbl3epMI1MAF2fyDuHlN1jD8FkwWJoBt8RkIkyegUzBa6kGalD2E1VT+6IDmBn3tJAaVdu48qn3C/Iekkef3wHP0s+pFUIxeNyUyyBHHJ+E6yGDAumsoJHvOfw+PX4eATM3PeEUVf3JYXckk5qC7oKC+faRUQa9WITdS2eYplPCHLYVyDc6Ewd8jxCkANGIEY1L3fxIIA9IRAI7ek8z6EZzIXQiB6I4+mNS/jfdSu6CwBkt/NoELXQabvWH1llKjzS187oANexample 4
Suppose a surface \(S\) is the graph of a differentiable function \(g\colon\, {\mathbb R}^2\to {\mathbb R}\). Write \(S\) in parametric form and show that the surface is smooth at all points \((u_0,v_0,g(u_0,v_0))\in {\mathbb R}^3\).
solution Write \(S\) in parametric form as follows: \[ x=u,\qquad y=v,\qquad z=g(u,v), \] which is the same as \(z=g(x, y)\). Then at the point \((u_0, v_0)\), \[ {\bf T}_u = {\bf i}+\frac{\partial g}{\partial u}(u_0,v_0){\bf k} \qquad \hbox{and} \qquad {\bf T}_v = {\bf j}+\frac{\partial g}{\partial v}(u_0,v_0){\bf k}, \] and for \((u_0,v_0)\in {\mathbb R}^2\), \begin{equation*} {\bf n}={\bf T}_u\times {\bf T}_v=-\frac{\partial g}{\partial u}(u_0,v_0){\bf i}-\frac{\partial g}{\partial v}(u_0,v_0){\bf j}+ {\bf k}\neq {\bf 0}.\tag{2} \end{equation*}
This is nonzero because the coefficient of \({\bf k}\) is 1; consequently, the parametrization \((u,v)\mapsto (u,v,g(u,v))\) is regular at all points. Moreover, the tangent plane at the point \((x_0,y_0,z_0) = (u_0,v_0, g(u_0,v_0))\) is given, by formula (1), as \[ (x-x_0,y-y_0,z-z_0)\, {\cdot}\, \bigg(\!\!{-}\frac{\partial g}{\partial u},-\frac{\partial g}{\partial v},1\bigg)=0, \] where the partial derivatives are evaluated at \((u_0,v_0)\). Remembering that \(x = u\) and \(y = v\), we can write this as \begin{equation*} z-z_0=\bigg(\frac{\partial g}{\partial x}\bigg)(x-x_0)+ \bigg(\frac{\partial g}{\partial y}\bigg)(y-y_0),\tag{3} \end{equation*} where \(\partial g/\partial x\) and \(\partial g/\partial y\) are evaluated at \((x_0, y_0)\).
This example also shows that the definition of the tangent plane for parametrized surfaces agrees with the one for surfaces obtained as graphs, because equation (3) is the same formula we derived (in Chapter 13) for the plane tangent to \(S\) at the point \((x_0,y_0,z_0) \in S\).
381
It is also useful to consider piecewise smooth surfaces, that is, surfaces composed of a certain number of images of smooth parametrized surfaces. For example, the surface of a cube in \({\mathbb R}^3\) is such a surface. These surfaces are considered in Section 17.4.
example 5
Find a parametrization for the hyperboloid of one sheet: \[ x^2+y^2-z^2=1 . \]
solution Because \(x\) and \(y\) appear in the combination \(x^2 + y^2\), the surface is invariant under rotation about the \(z\) axis, and so it is natural to write \[ x=r\cos \theta,\qquad y = r \sin \theta. \]
Then \(x^2+y^2-z^2=1\) becomes \(r^2-z^2=1\). This we can conveniently parametrize byfootnote # \[ r=\hbox{cosh }u,\qquad z=\hbox{sinh }u. \]
Thus, a parametrization is \[ x = \hbox{(cosh }u)(\cos \theta), \qquad y = \hbox{(cosh }u)(\sin \theta),\qquad z = \hbox{sinh }u, \] where \(0\leq \theta <2 \pi,-\infty < u < \infty\).