Question 17.61

\(x=2u,\qquad y=u^2+v,\qquad z=v^2,\qquad at\, (0,1,1)\)

Question 17.62

\(x=u^2-v^2,\qquad y=u+v,\qquad z=u^2+4v, at\, (-\frac{1}{4},\frac{1}{2},2)\)

Question 17.63

\(x=u^2,\qquad y=u\sin e^v,\qquad z=\frac{1}{3}u\cos e^v, at\, (13,-2,1)\)

Question 17.64

At what points are the surfaces in Exercises 1 and 2 regular?

Question 17.65

\(\Phi(u,v) = (u^2 - v^2, u^2 + v^2, v)\)

Question 17.66

\(\Phi(u,v) = (u - v, u + v, 2uv)\)

Question 17.67

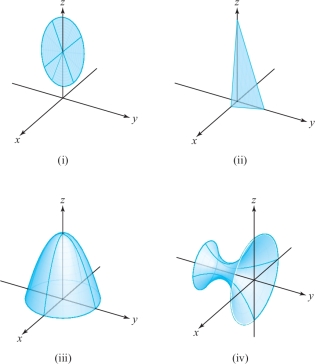
Match the following parameterizations to the surfaces shown in the figures.

• (a) \(\Phi(u,v) = ( (2 \sqrt{1+u^2}) \cos v, (2 \sqrt{1+u^2}) \sin v, u )\)
• (b) \(\Phi(u,v) = ( 3 \cos u \sin v, 2 \sin u \sin v, \cos v )\)
• (c) \(\Phi(u,v) = ( u,v,u^2 )\)
• (d) \(\Phi(u,v) = ( u \cos v, u \sin v, u )\)

Question 17.68

Match the following parametrizations to the surfaces shown in the figures.

• (a) \(\Phi(u,v) = ( u \cos v, u \sin v, 4 - u \cos v - u \sin v ); u \in [0,1], v \in [0, 2\pi]\)
• (b) \(\Phi(u,v) = ( u \cos v, u \sin v, 4 - u^2 )\)
• (c) \(\Phi(u,v) = ( u, v, \frac{1}{3}(12 - 8u - 3v) )\)
• (d) \(\Phi(u,v) = ( (u^2 + 6u + 11) \cos v, u, (u^2 + 6u + 11) \sin v )\)

Question 17.69

Find an expression for a unit vector normal to the surface \[ x=\cos v\sin u,\qquad y=\sin v \sin u,\qquad z=\cos u \] at the image of a point \((u,v)\) for \(u\) in \([0,\pi]\) and \(v\) in \([0,2\pi]\). Identify this surface.

Question 17.70

Repeat the previous exercise (the ninth) for the surface \[ x=3\cos \theta\sin \phi,\qquad y=2\sin \theta\sin \phi,\qquad z=\cos \phi \] for \(\theta\) in \([0, 2\pi]\) and \(\phi\) in \([0,\pi]\).

Question 17.71

Repeat the ninth exercise for the surface \[ x=\sin v,\qquad y=u,\qquad z=\cos v \] for \(0\leq v\leq 2\pi\) and \(-1\leq u\leq 3\).

Question 17.72

Repeat the ninth exercise for the surface \[ x=(2-\cos v)\cos u,\quad y=(2-\cos v)\sin u,\quad z=\sin v \] for \(-\pi \leq u\leq \pi,-\pi \leq v\leq \pi\). Is this surface regular?

Question 17.73

• (a) Develop a formula for the plane tangent to the surface \(x=h(y,z)\).
• (b) Obtain a similar formula for \(y=k(x,z)\).

Question 17.74

Find the equation of the plane tangent to the surface \(x=u^2,y=v^2,z=u^2+v^2\) at the point \(u=1,v=1\).

Question 17.75

Find a parametrization of the surface \(z=3x^2+8{\it xy}\) and use it to find the tangent plane at \(x=1,y=0,z=3\). Compare your answer with that using graphs.

Question 17.76

Find a parametrization of the surface \(x^3\,{+}\,3{\it xy} \,{+}\,z^2\,{=}\,2, z>0\), and use it to find the tangent plane at the point \(x\,{=}\,1,y\,{=}\,1/3,z\,{=}\,0\). Compare your answer with that using level sets.

Question 17.77

Consider the surface in \({\mathbb R}^3\) parametrized by \begin{eqnarray*} &&{\Phi}(r,\theta)=(r\cos \theta,r\sin \theta,\theta),\quad 0\leq r\leq 1\\ && \hbox{and}\quad 0\leq \theta \leq 4\pi. \end{eqnarray*}

• (a) Sketch and describe the surface.
• (b) Find an expression for a unit normal to the surface.
• (c) Find an equation for the plane tangent to the surface at the point \((x_0, y_0, z_0)\).
• (d) If \((x_0,y_0,z_0)\) is a point on the surface, show that the horizontal line segment of unit length from the \(z\) axis through \((x_0,y_0,z_0)\) is contained in the surface and in the plane tangent to the surface at \((x_0,y_0,z_0)\).

383

Question 17.78

Given a sphere of radius 2 centered at the origin, find the equation for the plane that is tangent to it at the point \((1,1,{\textstyle\sqrt{2})}\) by considering the sphere as:

• (a) a surface parametrized by \({\Phi}(\theta,\phi)= (2\cos \theta \sin \phi,2\sin \theta \sin \phi,2\cos \phi) \);
• (b) a level surface of \(f(x,y,z)=x^2+y^2+z^2 \); and
• (c) the graph of \(g(x,y)=\sqrt{4-x^2-y^2}\).

Question 17.79

• (a) Find a parametrization for the hyperboloid \(x^2 + y^2 - z^2 = 25\).
• (b) Find an expression for a unit normal to this surface.
• (c) Find an equation for the plane tangent to the surface at \((x_0,y_0,0)\), where \(x^2_0+y^2_0=25\).
• (d) Show that the lines \((x_0,y_0,0)+t(-y_0,x_0,5)\) and \((x_0,y_0,0)+t(y_0,-x_0,5)\) lie in the surface and in the tangent plane found in part (c).

Question 17.80

A parametrized surface is described by a differentiable function \({\Phi}\colon\, {\mathbb R}^2\to {\mathbb R}^3\). According to Chapter 13, the derivative should give a linear approximation that yields a representation of the tangent plane. This exercise demonstrates that this is indeed the case.

• (a) Assuming \({\bf T}_u \times {\bf T}_v\neq {\bf 0}\), show that the range of the linear transformation \({\bf D}{\Phi}(u_0,v_0)\) is the plane spanned by \({\bf T}_u\) and \({\bf T}_v.\,[\)Here \({\bf T}_u\) and \({\bf T}_v\) are evaluated at \((u_0,v_0)\).]
• (b) Show that \({\bf w}\,\bot \,({\bf T}_u \times {\bf T}_v \)) if and only if \({\bf w}\) is in the range of \({\bf D}{\Phi}(u_0,v_0)\).
• (c) Show that the tangent plane as defined in this section is the same as the “parametrized plane” \[ (u,v)\mapsto {\Phi}(u_0,v_0)+{\bf D}{\Phi}(u_0,v_0)\Big[ \begin{array}{c} u-u_0\\ v-v_0 \end{array}\Big]. \]

Question 17.81

Consider the surfaces \({\Phi}_1(u,v)=(u,v,0)\) and \({\Phi}_2(u,v)=(u^3,v^3,0)\).

• (a) Show that the image of \({\Phi}_1\) and of \({\Phi}_2\) is the \({\it xy}\) plane.
• (b) Show that \({\Phi}_1\) describes a regular surface, yet \({\Phi}_2\) does not. Conclude that the notion of regularity of a surface \(S\) depends on the existence of at least one regular parametrization for \(S\).
• (c) Prove that the tangent plane of \(S\) is well defined independently of the regular (one-to-one) parametrization (you will need to use the inverse function theorem from Section 14.5).
• (d) After these remarks, do you think you can find a regular parametrization of the cone of Figure 17.28?

Question 17.82

The image of the parametrization \begin{eqnarray*} \Phi(u,v) & = &( x(u,v),y(u,v),z(u,v) ) \\[3pt] & = &( a \sin u \cos v, b \sin u \sin v, c \cos u )\\[-16pt] \end{eqnarray*} with \(b<a\), \(0 \leq u \leq \pi\), \(0 \leq v \leq 2\pi\) parametrizes an ellipsoid.

• (a) Show that all points in the image of \(\Phi\) satisfy: \[ \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}} = 1 \] (the Cartesian equation of an ellipsoid).
• (b) Show that the image surface is regular at all points.

Question 17.83

The image of the parametrization \begin{eqnarray*} \Phi(u,v) & = &( x(u,v),y(u,v),z(u,v) ) \\[3pt] & = &( (R + r \cos u) \cos v, (R + r \cos u) \sin v, r \sin u ) \end{eqnarray*} with \(0 \leq u, v \leq 2\pi\), \(0< r <1\) parametrizes a torus (or doughnut) \(S\).

• (a) Show that all points in the image \((x,y,z)\) satisfy: \[ ( \sqrt{x^{2}+ y^{2}} - R)^2 + z^2 = r^2. \]
• (b) Show that the image surface is regular at all points.

Question 17.84

Let \({\Phi}\) be a regular surface at \((u_0,\!v_0)\); that is, \({\Phi}\) is of class \(C^1\) and \({\bf T}_u\!\times\!{\bf T}_v\!\neq\! {\bf 0}\) at \((u_0,\!v_0)\).

• (a) Use the implicit function theorem (Section 3.5) to show that the image of \({\Phi}\) near \((u_0,v_0)\) is the graph of a \(C^1\) function of two variables. If the \(z\) component of \({\bf T}_u\times {\bf T}_v\) is nonzero, we can write it as \(z = f(x, y)\).
• (c) Show that the tangent plane at \({\Phi}(u_0,v_0)\) defined by the plane spanned by \({\bf T}_u\) and \({\bf T}_v\) coincides with the tangent plane of the graph of \(z = f(x, y)\) at this point.