Question 17.87

Find the surface area of the unit sphere \(S\) represented parametrically by \({\Phi}\colon\, D\to S\subset {\mathbb R}^3\), where \(D\) is the rectangle \(0\leq \theta \leq 2\pi,0\leq \phi \leq \pi\) and \({\Phi}\) is given by the equations \[ x=\cos \theta \sin \phi,\qquad y=\sin\theta\sin\phi, \qquad z=\cos \phi. \]

Note that we can represent the entire sphere parametrically, but we cannot represent it in the form \(z=f(x,y)\).

Question 17.88

In the previous exercise, what happens if we allow \(\phi\) to vary from \(-\pi/2\) to \(\pi/2 \)? From 0 to \(2\pi\)? Why do we obtain different answers?

Question 17.89

Find the area of the helicoid in Example 2 if the domain \(D\) is \(0\leq r\leq 1\) and \(0\leq \theta \leq 3\pi\).

Question 17.90

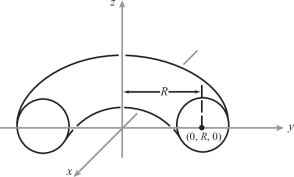
The torus \(T\) can be represented parametrically by the function \({\Phi}\colon\, D\to {\mathbb R}^3\), where \({\Phi}\) is given by the coordinate functions \(x=(R+\cos \phi)\cos \theta, y=(R+\cos \phi)\sin \theta,z=\sin \phi \); \(D\) is the rectangle \([0,2\pi]\times [0,2\pi]\), that is, \(0\leq \theta \leq 2\pi,0\leq \phi\leq 2\pi \); and \(R > 1\) is fixed (see Figure 17.35). Show that \(A(T)=(2\pi)^2R\), first by using formula (3) and then by using formula (6).

Question 17.91

Let \(\Phi(u,v) = ( e^u \cos v, e^u \sin v, v )\) be a mapping from \(D = [0,1] \times [0,\pi]\) in the \(uv\) plane onto a surface \(S\) in \({\it xyz}\) space.

• (a) Find \(T_u \times T_v\).
• (b) Find the equation for the tangent plane to \(S\) when \((u,v) = (0,\frac{\pi}{2})\).
• (c) Find the area of \(\Phi(D)\).

Question 17.92

Find the area of the surface defined by \(z={\it xy}\) and \(x^{2}+ y^{2} \leq 2\).

Question 17.93

Use a surface integral to find the area of the triangle \(T\) in \(\mathbb R^3\) with vertices at \((1,1,0)\), \((2,1,2)\), and \((2,3,3)\). Verify your answer by finding the lengths of the sides and using classical geometry. [HINT: Write the triangle as the graph \(z=g(x,y)\) over a triangle \(T^*\) in the \({\it xy}\) plane.]

Question 17.94

Use a surface integral to find the area of the quadrilateral \(D\) in \(\mathbb R^3\) with vertices at \((-1,1,2)\), \((1,1,2)\), \((0,3,5)\), and \((5,3,5)\). Verify your answer by finding the lengths of the sides and using classical geometry. [HINT: See the hint in the previous problem.]

Question 17.95

Let \({\Phi}(u,v)=(u-v,u+v,uv)\) and let \(D\) be the unit disc in the \(uv\) plane. Find the area of \({\Phi}(D)\).

Question 17.96

Find the area of the portion of the unit sphere that is cut out by the cone \(z\geq \sqrt{x^2+y^2}\) (see Exercise 1).

Question 17.97

Show that the surface \(x=1/\sqrt{y^2+z^2}\), where \(1\leq x<\infty\), can be filled but not painted!

Question 17.98

Find a parametrization of the surface \(x^2-y^2=1\), where \(x>0,-1\leq y\leq 1\) and \(0\leq z\leq 1\). Use your answer to express the area of the surface as an integral.

Question 17.99

Represent the ellipsoid \(E\): \[ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \] parametrically and write out the integral for its surface area \(A(E)\). (Do not evaluate the integral.)

392

Question 17.100

Let the curve \(y=f(x),a\leq x\leq b\), be rotated about the \(y\) axis. Show that the area of the surface swept out is given by equation (6); that is, \[ A=2\pi \int^b_a |x|{\textstyle\sqrt{1+[f'(x)]^2} }\,{\it dx} . \] Interpret the formula geometrically using arc length and slant height.

Question 17.101

Find the area of the surface obtained by rotating the curve \(y=x^2,0\leq x\leq 1\), about the \(y\) axis.

Question 17.102

Use formula (4) to compute the surface area of the cone in Example 1.

Question 17.103

Find the area of the surface defined by \(x + y + z = 1, x^2 + 2y^2 \leq 1\).

Question 17.104

Show that for the vectors \({\bf T}_u\) and \({\bf T}_v\), we have the formula \[ \|{\bf T}_u\times {\bf T}_v\| = \sqrt{\Big[\frac{\partial (x,y)}{\partial (u,v)}\Big]^2+\Big[\frac{\partial (y,z)}{\partial (u,v)}\Big]^2+\Big[\frac{\partial (x,z)}{\partial (u,v)}\Big]^2}. \]

Question 17.105

Compute the area of the surface given by \begin{eqnarray*} && x=r\cos\theta, \qquad y=2r\cos \theta,\qquad z=\theta, \\ && 0\leq r\leq 1,\qquad 0\leq \theta \leq 2\pi.\\[-14pt] \end{eqnarray*} Sketch.

Question 17.106

Prove Pappus’ theorem: Let \({\bf c}\colon\, [a,b]\to {\mathbb R}^2\) be a \(C^1\) path whose image lies in the right half plane and is a simple closed curve. The area of the lateral surface generated by rotating the image of \({\bf c}\) about the \(y\) axis is equal to \(2\pi \bar x l ({\bf c})\), where \(\bar x\) is the average value of the \(x\) coordinates of points on \({\bf c}\) and \(l ( {\bf c} )\) is the length of \({\bf c}\). (See Exercises 16 to 19, Section 17.1, for a discussion of average values.)

Question 17.107

The cylinder \(x^2 + y^2 = x\) divides the unit sphere \(S\) into two regions \(S_1\) and \(S_2\), where \(S_1\) is inside the cylinder and \(S_2\) outside. Find the ratio of areas \(A(S_2)/A(S_1)\).

Question 17.108

Suppose a surface \(S\) that is the graph of a function \(z=f(x,y)\), where \((x, y)\in D\subset {\mathbb R}^2\) can also be described as the set of \((x, y, z)\in {\mathbb R}^3\) with \(F(x, y, z) = 0\) (a level surface). Derive a formula for \(A(S)\) that involves only \(F\).

Question 17.109

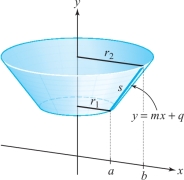
Calculate the area of the frustum shown in Figure 17.36 using (a) geometry alone and, second, (b) a surface-area formula.

Question 17.110

A cylindrical hole of radius 1 is bored through a solid ball of radius 2 to form a ring coupler, as shown in Figure 17.37. Find the volume and outer surface area of this coupler.

Question 17.111

Find the area of the graph of the function \(f(x,y)= \frac{2}{3}(x^{3/2}+y^{3/2})\) that lies over the domain \([0,1]\times [0,1]\).

Question 17.112

Express the surface area of the following graphs over the indicated region \(D\) as a double integral. Do not evaluate.

• (a) \((x+2y)^2;D=[-1,2]\times [0,2]\)
• (b) \({\it xy}+x/(y+1);D=[1,4]\times [1,2]\)
• (c) \({\it xy}^3e^{x^2y^2};D =\) unit circle centered at the origin
• (d) \(y^3\cos^2 x;D=\) triangle with vertices \((-1, 1), (0, 2)\), and \((1, 1)\)

Question 17.113

Show that the surface area of the upper hemisphere of radius \(R, z= \sqrt{R^2-x^2-y^2}\), can be computed by formula (4), evaluated as an improper integral.