18.5 Differential Forms

The theory of differential forms provides an elegant way of formulating Green’s, Stokes’, and Gauss’ theorems as one statement, the fundamental theorem of calculus. The birth of the concept of a differential form is another dramatic example of how mathematics speaks to mathematicians and drives its own development. These three theorems are, in reality, generalizations of the fundamental theorem of calculus of Newton and Leibniz for functions of one variable, \[ \int^b_a f^{\prime} (x)\, {\it {\,d} x}= f(b) - f(a) \] to two and three dimensions.

Recall that Bernhard Riemann created the concept of \(n\)-dimensional spaces. If the fundamental theorem of calculus was truly fundamental, then it should generalize to arbitrary dimensions. But wait! The cross product, and therefore the curl, does not generalize to higher dimensions, as we remarked in footnote 3, in Section 1.3. Thus, some new idea is needed.

Recall that Hamilton searched for almost 15 years for his quaternions, which ultimately led to the discovery of the cross product. What is the nonexistence of a cross product in higher dimensions telling us? If the fundamental theorem of calculus is the core concept, this suggests the existence of a mathematical language in which it can be formulated in \(n\)-dimensions. In order to achieve this, mathematicians realized that they were forced to move away from vectors and on to the discovery of dual vectors and an entirely new mathematical object, a differential form. In this new language, all of the theorems of Green, Stokes, and Gauss have the same elegant and extraordinarily simple form.

Simply and very briefly stated, an expression of the type \(P{\it {\,d} x} + Q\,{\it dy}\) is a 1-form, or a differential one-form on a region in the xy plane, and F dx dy is a 2-form. Analogously, we can define the notion of an \(n\)-form. There is an operation \(d\), which takes \(n\)-forms to \(n + 1\)-forms. It is like a generalized curl and has the property that for \(\omega = P\, {\it dx} + Q {\it dy}\), we have \[ d \omega = \left( \frac{\partial\! Q}{\partial x} - \frac{\partial\! P}{\partial y}\right)\!\! {\it {\,d} x}\, {\it dy} \] and so in this notation, Green’s theorem becomes \[ \int_{\partial\! D} \omega = \int_D d\omega, \] which, interestingly, just switches the boundary operator \(\partial\!\) with the \(d\) operator. However, differential forms are more than just notation. They create a beautiful theory that generalizes to \(n\)-dimensions.

In general, if \(M\) is an oriented surface of dimension \(n\) with an (\(n - 1\))-dimensional boundary \(\partial\! M\) and if \(\omega\) is an (\(n - 1\))-form on \(M\), then the fundamental theorem of calculus (also called the generalized Stokes’ theorem) reads \[ \fbox{{\(\displaystyle\int_{\partial\! M} \omega =\int _{M} d\omega\).}} \]

A useful thing for you to contemplate at this stage is the sense in which the fundamental theorem of calculus becomes a special instance of this result.

In this section, we shall give a very elementary exposition of the theory of forms. Because our primary goal is to show that the theorems of Green, Stokes, and Gauss can be unified under a single theorem, we shall be satisfied with less than the strongest possible version of these theorems. Moreover, we shall introduce forms in a purely axiomatic and nonconstructive manner, thereby avoiding the tremendous number of formal algebraic preliminaries that are usually required for their construction. To the purist our approach will be far from complete, but to the student it may be comprehensible. We hope that this will motivate some students to delve further into the theory of differential forms.

We shall begin by introducing the notion of a 0-form.

0-Forms

Let \(K\) be an open set in \({\mathbb R}^3\). A 0-form on \(K\) is a real-valued function \(f{:}\,K\to {\mathbb R}\). When we differentiate \(f\) once, it is assumed to be of class \(C^1\), and \(C^2\) when we differentiate twice.

Given two 0-forms \(f_1\) and \(f_2\) on \(K\), we can add them in the usual way to get a new 0-form \(f_1+f_2\) or multiply them to get a 0-form \(f_1f_2\).

1-Forms

The basic 1-forms are the expressions \({\it dx},{\it dy}\), and \(dz\). At present we consider these to be only formal symbols. A 1-form \(\omega\) on an open set \(K\) is a formal linear combination \[ \omega=P(x,y,z)\,{\it {\,d} x}+Q(x,y,z)\,{\it dy}+R(x,y,z){\,d} z, \] or simply \[ \omega=P{\it {\,d} x}+Q\,{\it dy}+R{\,d} z, \] where \(P,Q\), and \(R\) are real-valued functions on \(K\). By the expression \(P{\it {\,d} x}\) we mean the 1-form \(P{\it {\,d} x}+0\,{\cdot}\,{\it dy}+0\,{\cdot}\, {\,d} z\), and similarly for \(Q\,{\it dy}\) and \(R{\,d} z\). Also, the order of \(P{\it {\,d} x}, Q\,{\it dy}\), and \(R{\,d} z\) is immaterial, and so \[ P{\it {\,d} x}+Q\,{\it dy}+R{\,d} z=R{\,d} z+P{\it {\,d} x}+Q\,{\it dy}, \hbox{etc.} \]

Given two 1-forms \(\omega_1=P_1{\it {\,d} x}+Q_1{\it dy}+R_1{\,d} z\) and \(\omega_2=P_2{\it {\,d} x}+Q_2{\it dy}+R_2{\,d} z\), we can add them to get a new 1-form \(\omega_1+\omega_2\) defined by \[ \omega_1+\omega_2=(P_1+P_2)\,{\it {\,d} x}+(Q_1+Q_2)\,{\it dy}+(R_1+R_2){\,d} z, \] and given a 0-form \(f\), we can form the 1-form \(f\omega_1\) defined by \[ f\omega_1=(f\! P_1)\,{\it {\,d} x}+(f\! Q_1)\,{\it dy}+(f\! R_1){\,d} z. \]

2-Forms

The basic 2-forms are the formal expressions \({\it {\,d} x}\, {\it dy}, {\it dy} {\,d} z\), and \({\,d} z{\it {\,d} x}\). These expressions should be thought of as products of \({\it {\,d} x}\) and \({\it dy},{\it dy}\) and \({\,d} z\), and \({\,d} z\) and \({\it {\,d} x}\).

A 2-form \(\eta\) on \(K\) is a formal expression \[ \eta=F{\it {\,d} x}\,{\it dy}+G\,{\it dy}{\,d} z+H{\,d} z{\it {\,d} x}, \] where \(F,G\), and \(H\) are real-valued functions on \(K\). The order of \(F{\it {\,d} x}\,{\it dy}, G\,{\it dy}{\,d} z\), and \(H{\,d} z{\it {\,d} x}\) is immaterial; for example, \[ F{\it {\,d} x}\,{\it dy}+G\,{\it dy}\,{\,d} z+H{\,d} z{\it {\,d} x}=H{\,d} z\,{\it {\,d} x}+F{\it {\,d} x}\,{\it dy}+G\,{\it dy}\,{\,d} z,\hbox{etc.} \]

At this point it is useful to note that in a 2-form the basic 1-forms \({\it {\,d} x},{\it dy}\), and \(dz\) always appear in cyclic pairs (see Figure 18.42), that is, \({\it {\,d} x}\,{\it dy},{\it dy}\,{\,d} z\), and \({\,d} z{\it {\,d} x}\).

By analogy with 0-forms and 1-forms, we can add two 2-forms \[ \eta_i=F_i{\it {\,d} x}\,{\it dy}+G_i\,{\it dy}\,{\,d} z+H_i{\,d} z{\it {\,d} x}, \] \(i =1\) and 2, to obtain a new 2-form, \[ \eta_1+\eta_2=(F_1+F_2)\,{\it {\,d} x}\,{\it dy}+ (G_1 +G_2)\, {\it dy}\, {\,d} z + (H_1 + H_2) {\,d} z {\it {\,d} x}. \]

Similarly, if \(f\) is a 0-form and \(\eta\) is a 2-form, we can take the product \[ f\! \eta=(f\! F)\,{\it {\,d} x}\,{\it dy}+(f\! G)\,{\it dy}\,{\,d} z+(f\! H){\,d} z{\it {\,d} x}. \]

Finally, by the expression \(F{\it {\,d} x}\,{\it dy}\) we mean the 2-form \(F{\it {\,d} x}\,{\it dy}+0\,{\cdot}\, {\it dy}\,{\,d} z+0\,{\cdot}\, {\,d} z{\it {\,d} x}\).

3-Forms

A basic 3-form is a formal expression \({\it {\,d} x}\,{\it dy}\,{\,d} z\) (in this specific cyclic order, as in Figure 18.42). A 3-form \(\nu\) on an open set \(K\subset {\mathbb R}^3\) is an expression of the form \(\nu=f(x,y,z)\,{\it {\,d} x}\,{\it dy}\,{\,d} z\), where \(f\) is a real-valued function on \(K\).

We can add two 3-forms and we can multiply them by 0-forms in the obvious way. There seems to be little difference between a 0-form and a 3-form, because both involve a single real-valued function. But we distinguish them for a purpose that will become clear when we multiply and differentiate forms.

Although we can add two 0-forms, two 1-forms, two 2-forms, or two 3-forms, we do not need to add a \(k\)-form and a \(j\)-form if \(k\neq j\). For example, we shall not need to write \[ f(x,y,z)\,{\it {\,d} x}\,{\it dy}+g\,(x,y,z){\,d} z. \]

Now that we have defined these formal objects (forms), we can legitimately ask what they are good for, how they are used, and, perhaps most important, what they mean. The answer to the first question will become clear as we proceed, but we can immediately describe how to use and interpret them.

A real-valued function on a domain \(K\) in \({\mathbb R}^3\) is a rule that assigns a real number to each point in \(K\). Differential forms are, in some sense, generalizations of the real-valued functions we have studied in calculus. In fact, 0-forms on an open set \(K\) are just functions on \(K\). Thus, a 0-form \(f\) takes points in \(K\) to real numbers.

We should like to interpret differential \(k\)-forms (for \(k\geq 1\)) not as functions on points in \(K\), but as functions on geometric objects such as curves and surfaces. Many of the early Greek geometers viewed lines and curves as being made up of infinitely many points, and planes and surfaces as being made up of infinitely many curves. Consequently, there is at least some historical justification for applying this geometric hierarchy to the interpretation of differential forms.

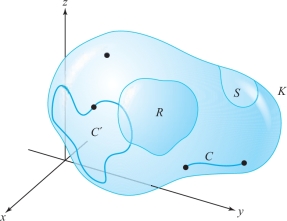
Given an open subset \(K\subset {\mathbb R}^3\), we shall distinguish four types of subsets of \(K\) (see Figure 18.43):

• (i) points in \(K\),
• (ii) oriented simple curves and oriented simple closed curves, \(C\), in \(K\),
• (iii) oriented surfaces, \(S\subset K\),
• (iv) elementary subregions, \(R\subset K\).

The Integral of 1-Forms Over Curves

We shall begin with 1-forms. Let \[ \omega=P(x,y,z)\,{\it {\,d} x}+Q(x,y,z)\,{\it dy}+R(x,y,z){\,d} z \] be a 1-form on \(K\) and let \(C\) be an oriented simple curve as in Figure 18.44. The real number that \(\omega\) assigns to \(C\) is given by the formula \begin{equation*} \int_C\omega=\int_CP(x,y,z)\,{\it {\,d} x}+Q(x,y,z)\,{\it dy}+R(x,y,z){\,d} z.\tag{1} \end{equation*}

Recall (see Section 7.2) that this integral is evaluated as follows. Suppose that \({\bf c}{:}\,[a,b]\to K, {\bf c}(t)=(x(t),y(t),z(t))\) is an orientation-preserving parametrization of \(C\). Then \begin{eqnarray*} \int_C\omega=\int_{\bf c}\omega &=& \int_a^b\bigg[P(x(t),y(t),z(t)) \,{\cdot}\,\frac{{\it dx}}{{\it dt}}\\[4pt] &&\quad + Q(x(t),y(t),z(t))\,{\cdot}\,\frac{{\it dy}}{{\it dt}} + R(x(t),y(t),z(t))\,{\cdot}\,\frac{dz}{{\it dt}}\bigg]\,{\it dt}. \end{eqnarray*}

Theorem 1 of Section 7.2 guarantees that \(\int_C\omega\) does not depend on the choice of the parametrization \({\bf c}\).

We can thus interpret a 1-form \(\omega\) on \(K\) as a rule assigning a real number to each oriented curve \(C\subset K\); a 2-form \(\eta\) will similarly be seen to be a rule assigning a real number to each oriented surface \(S\subset K\); and a 3-form \(\nu\) will be a rule assigning a real number to each elementary subregion of \(K\). The rules for associating real numbers with curves, surfaces, and regions are completely contained in the formal expressions we have defined.

The Integral of 2-Forms Over Surfaces

A 2-form \(\eta\) on an open set \(K\subset {\mathbb R}^3\) can similarly be interpreted as a function that associates a real number with each oriented surface \(S\subset K\). This is accomplished by means of the notion of integration of 2-forms over surfaces. Let \[ \eta=F(x,y,z)\,{\it {\,d} x}\,{\it dy}+G(x,y,z)\,{\it dy}\,{\,d} z+H(x,y,z){\,d} z{\it {\,d} x} \] be a 2-form on \(K\), and let \(S\subset K\) be an oriented surface parametrized by a function \({\Phi}{:}\,D\to {\mathbb R}^3\), \(D\subset {\mathbb R}^2,{\Phi}(u,v)=(x(u,v),y(u,v),z(u,v))\) (see Section 7.3).

The Integral of 3-Forms Over Regions

Finally, we must interpret 3-forms as functions on the elementary subregions of \(K\). Let \(v =f(x,y,z)\,{\it {\,d} x}\,{\it dy}\,{\,d} z\) be a 3-form and let \(R\subset K\) be an elementary subregion of \(K\). Then to each such \(R\subset K\) we assign the number \begin{equation*} \intop\!\!\!\intop\!\!\!\intop\nolimits_{R} v =\intop\!\!\!\intop\!\!\!\intop\nolimits_{R}f(x,y,z)\,{\it {\,d} x}\,{\it dy}\,{\,d} z,\tag{3} \end{equation*} which is just the ordinary triple integral of \(f\) over \(R\), as described in Section 5.5.

The Algebra of Forms

We now discuss the algebra (or rules of multiplication) of forms that, together with differentiation of forms, will enable us to state Green’s, Stokes’, and Gauss’ theorems in terms of differential forms.

If \(\omega\) is a \(k\)-form and \(\eta\) is an \(l\)-form on \(K,0\leq k+l\leq 3\), there is a product called the wedge product \(\omega \wedge \eta\) of \(\omega\) and \(\eta\) that is a \(k+l\) form on \(K\). The wedge product satisfies the following laws:

• (i) For each \(k\) there is a zero \(k\)-form 0 with the property that \(0+\omega=\omega\) for all \(k\)-forms \(\omega\) and \(0\wedge\eta=0\) for all \(l\)-forms \(\eta\) if \(0\leq k+l\leq 3\).
• (ii) (Distributivity) If \(f\) is a 0-form, then \[ (f\omega_1+\omega_2)\wedge \eta=f(\omega_1\wedge\eta)+(\omega_2\wedge\eta). \]
• (iii) (Anticommutativity) \(\omega\wedge\eta=(-1)^{kl}(\eta\wedge\omega)\).
• (iv) (Associativity) If \(\omega_1,\omega_2,\omega_3\) are \(k_1,k_2,k_3\) forms, respectively, with \(k_1 + k_2 + k_3\leq 3\), then \[ \omega_1\wedge(\omega_2\wedge\omega_3)=(\omega_1\wedge\omega_2)\wedge\omega_3. \]
• (v) (Homogeneity with respect to functions) If \(f\) is a 0-form, then \[ \omega\wedge(f\eta)=(f\omega)\wedge\eta=f(\omega\wedge\eta). \] Notice that rules (ii) and (iii) actually imply rule (v).
• (vi) The following multiplication rules for 1-forms hold: \begin{eqnarray*} &&\displaystyle {\it {\,d} x}\wedge {\it dy} = {\it {\,d} x}\,{\it dy}\\[2pt] &&\displaystyle {\it dy}\wedge {\it {\,d} x} =-{\it {\,d} x}\,{\it dy} =(-1)({\it {\,d} x}\wedge {\it dy})\\[2pt] &&\displaystyle {\it dy}\wedge {\,d} z = {\it dy}\,{\,d} z =(-1)({\,d} z\wedge {\it dy})\\[2pt] &&\displaystyle {\,d} z\wedge {\it {\,d} x} = {\,d} z\,{\it {\,d} x} =(-1)({\it {\,d} x}\wedge {\,d} z)\\[2pt] &&\displaystyle{\it {\,d} x}\wedge {\it {\,d} x}=0,\ {\it dy}\wedge{\it dy}=0,\ {\,d} z\,\wedge {\,d} z =0\\[2pt] &&\displaystyle {\it {\,d} x}\wedge ({\it dy}\wedge {\,d} z) = ({\it {\,d} x}\wedge {\it dy})\wedge{\,d} z= {\it {\,d} x}\,{\it dy}{\,d} z. \end{eqnarray*}
• (vii) If \(f\) is a 0-form and \(\omega\) is any \(k\)-form, then \(f\wedge\omega=f\omega\).

Using laws (i) to (vii), we can now find a unique product of any \(l\)-form \(\eta\) and any \(k\)-form \(\omega\), if \(0\leq k+l \leq 3\).

The last major step in the development of this theory is to show how to differentiate forms. The derivative of a \(k\)-form is a \((k+1)\)-form if \(k<3\), and the derivative of a 3-form is always zero. If \(\omega\) is a \(k\)-form, we shall denote the derivative of \(\omega\) by \(d\omega\). The operation \(d\) has the following properties:

(1) If \(f{:}\,K\to {\mathbb R}\) is a 0-form, then \[ {\,d} f=\frac{\partial\! f}{\partial x}{\it {\,d} x}+\frac{\partial\! f}{\partial y}{\it dy}+\frac{\partial\! f}{\partial z}{\,d} z. \]

(2)(Linearity) If \(\omega_1\) and \(\omega_2\) are \(k\)-forms, then \[ d(\omega_1+\omega_2)={\,d} \omega_1+{\,d} \omega_2. \]

(3) If \(\omega\) is a \(k\)-form and \(\eta\) is an \(l\)-form, \[ d(\omega\wedge\eta)=(d\omega\wedge\eta)+(-1)^k(\omega\wedge d\eta). \]

(4) \(d(d\omega)=0\) and \(d({\it dx})=d({\it dy})=d(dz)=0\) or, simply, \(d^2=0\).

Properties (1) to (4) provide enough information to allow us to uniquely differentiate any form.

We have now developed all the concepts needed to reformulate Green’s, Stokes’, and Gauss’ theorems in the language of forms.

Here \(d\omega\) is a 2-form on \(K\) and \(D\) is in fact a surface in \({\mathbb R}^3\) parametrized by \({\Phi}{:}\,D\to {\mathbb R}^3, {\Phi}(x,y)=(x,y,0)\). Because \(P\) and \(Q\) are explicitly not functions of \(z\), then \(\partial\! P/\partial z\) and \(\partial\! Q/\partial z=0\), and by Example 12, \(d\omega=(\partial\! Q/\partial x-\partial\! P/\partial y)\,{\it {\,d} x}\,{\it dy}\). Consequently, Theorem 13 means nothing more than that \[ \int_{\partial\! D}P {\it {\,d} x}+Q\,{\it dy}=\intop\!\!\!\intop\nolimits_{D}\left( \frac{\partial\! Q}{\partial x}-\frac{\partial\! P}{\partial y}\right)\,{\it dx}\,{\it dy}, \] which is precisely Green’s theorem. Hence, Theorem 13 holds. Likewise, we have the following theorems.

The reader has probably noticed the strong similarity in the statements of these theorems. In the vector-field formulations, we used divergence for regions in \({\mathbb R}^3\) (Gauss’ theorem) and the curl for surfaces in \({\mathbb R}^3\) (Stokes’ theorem) and regions in \({\mathbb R}^2\) (Green’s theorem). Here we just use the unified notion of the derivative of a differential form for all three theorems; and, in fact, we can state all theorems as one by introducing a little more terminology.

By an oriented 2-manifold with boundary in \({\mathbb R}^3\) we mean a surface in \({\mathbb R}^3\) whose boundary is a simple closed curve with orientation as described in Section 18.2. By an oriented 3-manifold in \({\mathbb R}^3\) we mean an elementary region in \({\mathbb R}^3\) (we assume its boundary, which is a surface, is given the outward orientation discussed in Section 18.4). We call the following unified theorem “Stokes’ theorem,” according to the current convention.

Here the integral is interpreted as a single, double, or triple integral, as is appropriate. In fact, it is this form of Stokes’ theorem that generalizes to spaces of arbitrary dimension.