TOOLS OF THE ASTRONOMER’S TRADE

Calculating Tidal Forces

The gravitational force between any two objects decreases with increasing distance between the objects. This principle leads to a simple formula for estimating the tidal force that Earth exerts on parts of the Moon.

Consider two small objects, each of mass m, on opposite sides of the Moon. Because the two objects are at different distances from Earth’s center, Earth exerts different forces F_near and F_far on them (see the accompanying illustration). The consequence of this difference is that the two objects tend to pull away from each other and away from the center of the Moon (see Section 4-8, especially Figure 4-26). The tidal force on these two objects, which is the force that tends to pull them apart, is the difference between the forces on the individual objects:

Both F_near and F_far are inversely proportional to the square of the distance from Earth (see Section 4-7). If this distance were doubled, both forces would decrease to ½² = ¼ of their original values. But the tidal force F_tidal, which is the difference between these two forces, decreases even more rapidly with distance: It is inversely proportional to the cube of the distance from Earth to the Moon. That is, doubling the Earth-Moon distance decreases the tidal force to ½³ = ⅛ of its original value. If we use the symbols M_Earth for Earth’s mass (5.974 × 10²⁴ kg), d for the Moon’s diameter, r for the center-to-center distance from Earth to the Moon, and G for the universal constant of gravitation (6.67 × 10⁻¹¹ newton m²/kg²), the tidal force is given approximately by the formula

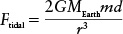
EXAMPLE: Calculate the tidal force for two 1-kg lunar rocks at the locations shown in the figure.

Situation: We are asked to calculate a tidal force. We know the masses of Earth (M_Earth) and of each of the two rocks (m = 1 kg). The Earth-Moon distance (r) and the diameter of the Moon (d, equal to the separation between the two rocks) are given in Table 10-1.

Tools: We use the equation given above for the tidal force F_tidal.

Answer: To use the given values in the equation, we must first convert the values for the average Earth-Moon distance r and the Moon’s diameter d from kilometers to meters:

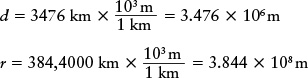
The tidal force is then

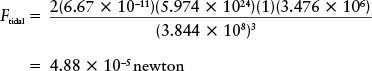
Review: To put our result into perspective, let us compare it to the weight of a 1-kg rock on the Moon. The weight of an object is equal to its mass multiplied by the acceleration due to gravity (see Section 4-6). This acceleration is equal to 9.8 m/s² on Earth, but is only 0.17 as great on the Moon. So, the weight of a 1-kg rock on the Moon is

Thus, the tidal force on lunar rocks is much less than their weight, which is a good thing. If the tidal force (which tries to pull a rock away from the Moon’s center) were greater than the weight (which pulls it toward the Moon’s center), loose objects would levitate off the Moon’s surface and fly into space!

The tidal force of Earth on the Moon deforms the solid body of the Moon, so that it acquires tidal bulges on its near and far sides. The mass of each bulge must be proportional to the tidal force that lifts lunar material away from the Moon’s center. So, the above formula tells us that the mass of each bulge is inversely proportional to the cube of the Earth-Moon distance r:

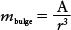
(Determining the value of the constant A requires knowing how easily the Moon deforms, which is a complicated problem beyond our scope.) We can then use our formula for the tidal force F_tidal to tell us the net tidal force on the Moon. To make this calculation, we think of the objects of mass m on opposite sides of the Moon as being the tidal bulges. So, we substitute m_βulge for m in the tidal force formula

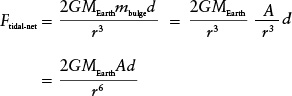
Thus, the net tidal force on the Moon is inversely proportional to the sixth power of the Earth-Moon distance. Even a small decrease in this distance can cause a substantial increase in the net tidal force.

EXAMPLE: Compare the net tidal force on the Moon at perigee (when it is closest to Earth) and at apogee (when it is farthest away).

Situation: We are asked to compare the tidal forces on the Moon at two different distances from Earth. To make this comparison, we will find the ratio of the tidal force at perigee to the tidal force at apogee.

Tools: We use the equation given above for the net tidal force on the Moon.

Answer: The Earth-Moon distances at perigee and apogee are given in Table 10-1. If we take the ratio of the tidal forces at these two distances, the constants (including the unknown quantity A) cancel out:

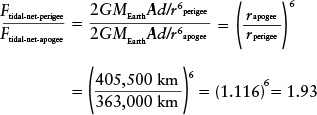
Review: Our result tells us that the net tidal force at perigee is 1.93 times as great (that is, almost double) as at apogee. Tidal forces on the Moon help create the stresses that generate moonquakes, so it is not surprising that these quakes are more frequent at perigee than at apogee.