TOOLS OF THE ASTRONOMER’S TRADE

Converting Mass into Energy

The Cosmic Connections: The Proton-Proton Chain figure shows the steps involved in the thermonuclear fusion of hydrogen at the Sun’s center. In these steps, four protons are converted into a single nucleus of ⁴He, the most common isotope of helium with two protons and two neutrons. (As we saw in Box 5-5, different isotopes of the same element have the same number of protons but different numbers of neutrons.) The reaction depicted in the Cosmic Connections Step 1 also produces a neutral, nearly massless particle called the neutrino. Neutrinos respond hardly at all to ordinary matter, so they travel almost unimpeded through the Sun’s massive bulk. Hence, the energy that neutrinos carry is quickly lost into space. This loss is not great, however, because the neutrinos carry relatively little energy. (See Section 16-4 for more about these curious particles.)

Most of the energy released by thermonuclear fusion appears in the form of gamma-ray photons. The energy of these photons remains trapped within the Sun for a long time, thus maintaining the Sun’s intense internal heat. Some gamma-ray photons are produced by the reaction shown as Step 2 in the Cosmic Connections figure. Others appear when an electron in the Sun’s interior annihilates a positively charged electron, or positron, which is a by-product of the reaction shown in Step 1 in the Cosmic Connections figure. An electron and a positron are respectively matter and antimatter, and they convert their mass entirely into energy when they meet. (You may have thought that “antimatter” was pure science fiction. In fact, tremendous amounts of antimatter are being created and annihilated in the Sun as you read these words.)

We can summarize the thermonuclear fusion of hydrogen as follows:

To calculate how much energy is released in this process, we use Einstein’s mass-energy formula: The energy released is equal to the amount of mass consumed multiplied by c², where c is the speed of light. To see how much mass is consumed, we compare the combined mass of four hydrogen atoms (the ingredients) to the mass of one helium atom (the product):

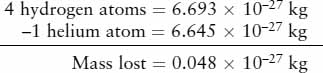
Thus, a small fraction (0.7%) of the mass of the hydrogen going into the nuclear reaction does not show up in the mass of the helium. This lost mass is converted into an amount of energy E = mc²:

This amount of energy is released by the formation of a single helium atom. It would light a 10-watt lightbulb for almost one-half of a trillionth of a second.

EXAMPLE: How much energy is released when 1 kg of hydrogen is converted to helium?

Situation: We are given the initial mass of hydrogen. We know that a fraction of the mass is lost when the hydrogen undergoes fusion to make helium; our goal is to find the quantity of energy into which this lost mass is transformed.

Tools: We use the equation E = mc² and the result that 0.7% of the mass is lost when hydrogen is converted into helium.

Answer: When 1 kg of hydrogen is converted to helium, the amount of mass lost is 0.7% of 1 kg, or 0.007 kg. (This means that 0.993 kg of helium is produced.) Using Einstein’s equation, we find that this missing 0.007 kg of matter is transformed into an amount of energy equal to

Review: The energy released by the fusion of 1 kg of hydrogen is the same as that released by burning 20,000 metric tons (2 × 10⁷ kg) of coal! Hydrogen fusion is a much more efficient energy source than ordinary burning.

The Sun’s luminosity is 3.9 × 10²⁶ joules per second. To generate this much power, hydrogen must be consumed at a rate of

That is, the Sun converts 600 million metric tons of hydrogen into helium every second.