TOOLS OF THE ASTRONOMER’S TRADE

Stellar Motions

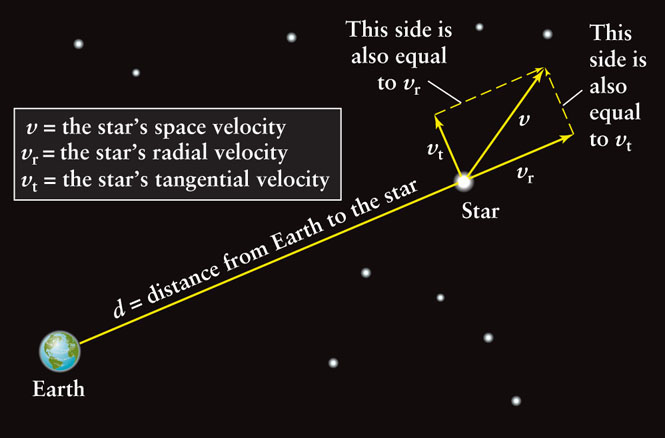
Stars can move through space in any direction. The space velocity of a star describes how fast and in what direction it is moving. As the accompanying figure shows, a star’s space velocity v can be broken into components parallel and perpendicular to our line of sight.

The component of velocity perpendicular to our line of sight—that is, across the plane of the sky—is called the star’s tangential velocity (v_t). To determine it, astronomers must know the distance to a star (d) and its proper motion (μ, the Greek letter mu), which is the number of arcseconds that the star appears to move per year on the celestial sphere. Proper motion does not repeat itself yearly, so it can be distinguished from the apparent back-and-forth motion due to parallax. In terms of a star’s distance and proper motion, its tangential velocity (in km/s) is

where μ is in arcseconds per year and d is in parsecs. For example, Barnard’s star (Figure 17-3) has a proper motion of 10.358 arcseconds per year and a distance of 1.83 pc. Hence, its tangential velocity is

The component of a star’s motion parallel to our line of sight—that is, either directly toward us or directly away from us—is its radial velocity (v_r). It can be determined from measurements of the Doppler shifts of the star’s spectral lines (see Section 5-9 and Box 5-6). If a star is approaching us, the wavelengths of all of its spectral lines are decreased (blueshifted); if the star is receding from us, the wavelengths are increased (redshifted). The radial velocity v_r is related to the wavelength shift by the equation

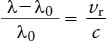
In this equation, λ is the wavelength of light coming from the star, λ₀ is what the wavelength would be if the star were not moving, and c is the speed of light. As an illustration, a particular spectral line of iron in the spectrum of Barnard’s star has a wavelength (λ) of 516.445 nm. As measured in a laboratory on Earth, the same spectral line has a wavelength (λ₀) of 516.629 nm. Thus, for Barnard’s star, our equation becomes

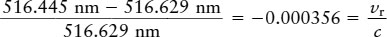
Solving this equation for the radial velocity v_r, we find

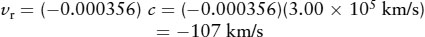
The minus sign means that Barnard’s star is moving toward us. You can check this interpretation by noting that the wavelength λ = 516.445 nm received from Barnard’s star is less than the laboratory wavelength λ₀ = 516.629 nm; hence, the light from the star is blueshifted, which indeed means that the star is approaching. If the star were receding, its light would be redshifted, and its radial velocity would be positive.

The illustration shows that the tangential velocity and radial velocity form two sides of a right triangle. The long side (hypotenuse) of this triangle is the space velocity (v). From the Pythagorean theorem, the space velocity is

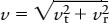
For Barnard’s star, the space velocity is

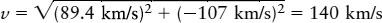
Therefore, Barnard’s star is moving through space at a speed of 140 km/s (503,000 km/h, or 312,000 mi/h) relative to the Sun.

Determining the space velocities of stars is essential for understanding the structure of the Galaxy. Studies show that the stars in our local neighborhood are moving in wide orbits around the center of the Galaxy, which lies some 8000 pc (26,000 ly) away in the direction of the constellation Sagittarius (the Archer). While many of the orbits are roughly circular and lie in nearly the same plane, others are highly elliptical or steeply inclined to the galactic plane. We will see in Chapter 22 how the orbits of stars and gas clouds reveal the Galaxy’s spiral structure.