TOOLS OF THE ASTRONOMER’S TRADE
Luminosity, Distance, and Apparent Brightness
The Inverse-square law (Section 17-2) relates a star’s luminosity, distance, and apparent brightness to the corresponding quantities for the sun:
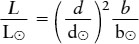
We can use a similar equation to relate the luminosities, distances, and apparent brightnesses of any two stars, which we call star 1 and star 2:
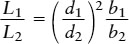
EXAMPLE: The star ε (epsilon) Eridani is 3.23 pc from Earth. As seen from Earth, this star appears only 6.73 × 10−13 as bright as the Sun. What is the luminosity of ε Eridani compared with that of the Sun?
Situation: We are given the distance to ε Eridani (d = 3.23 pc) and this star’s brightness compared to that of the Sun (b/b⊙ = 6.73 × 10−13). Our goal is to find the ratio of the luminosity of ε Eridani to that of the Sun, that is, the quantity L/L⊙.
Tools: Since we are asked to compare this star to the Sun, we use the first of the two equations given above, L/L⊙ = (d/d⊙)2(b/b⊙), to solve for L/L⊙.
Answer: Our equation requires the ratio of the star’s distance to the Sun’s distance, d/d⊙. The distance from Earth to the Sun is d⊙ = 1 AU. To calculate the ratio d/d⊙, we must express both distances in the same units. There are 206,265 AU in 1 pc, so we can write the distance to ε Eridani as d = (3.23 pc)(206,265 AU/pc) = 6.66 × 105 AU. Hence, the ratio of distances is d/d⊙ = (6.66 × 105 AU)/(1 AU) = 6.66 × 105. Then we find that the ratio of the luminosity of ε Eridani (L) to the Sun’s luminosity (L⊙) is
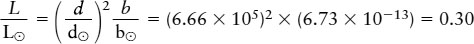
Review: This result means that ε Eridani is only 0.30 as luminous as the Sun; that is, its power output is only 30% as great.
EXAMPLE: Suppose star 1 is at half the distance of star 2 (that is, d1/d2 = ½) and that star 1 appears twice as bright as star 2 (that is, b1/b2 = 2). How do the luminosities of these two stars compare?
Situation: For these two stars, we are given the ratio of distances (d1/d2) and the ratio of apparent brightnesses (b1/b2). Our goal is to find the ratio of their luminosities (L1/L2).
Tools: Since we are comparing two stars, neither of which is the Sun, we use the second of the two equations above: L1/L2 = (d1/d2)2(b1/b2).
Answer: Plugging values into our equation, we find
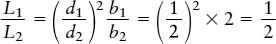
Review: This result says that star 1 has only one-half the luminosity of star 2. Despite this, star 1 appears brighter than star 2 because it is closer to us.
The two equations above are also useful in the method of spectroscopic parallax, which we discuss in Section 17-8. It turns out that a star’s luminosity can be determined simply by analyzing the star’s spectrum. If the star’s apparent brightness is also known, the star’s distance can be calculated. The inverse-square law can be rewritten as an expression for the ratio of the star’s distance from Earth (d) to the Earth-Sun distance (d⊙):
We can also use this formula as a relation between the properties of any two stars, 1 and 2:
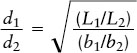
EXAMPLE: The star Pleione in the constellation Taurus is 190 times as luminous as the Sun but appears only 3.19 × 10−13 as bright as the Sun. How far is Pleione from Earth?
Situation: We are told the ratio of Pleione’s luminosity to that of the Sun (L/L⊙ = 190) and the ratio of their apparent brightnesses (b/b⊙ = 3.19 × 10−13). Our goal is to find the distance d from Earth to Pleione.
Tools: Since we are comparing Pleione to the Sun, we use the first of the two equations above.
Answer: Our equation tells us the ratio of the Earth-Pleione distance to the Earth-Sun distance:
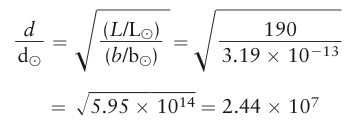
Hence, the distance from Earth to Pleione is 2.44 × 107 times greater than the distance from Earth to the Sun. The Sun-Earth distance is d⊙ = 1 AU and 206,265 AU = 1 pc, so we can express the star’s distance as d = (2.44 × 107 AU) × (1 pc/206,265 AU) = 118 pc.
Review: We can check our result by comparing it with the above example about the star ε Eridani. Pleione has a much greater luminosity than ε Eridani (190 times the Sun’s luminosity versus 0.30 times), but Pleione appears dimmer than ε Eridani (3.19 × 10−13 times as bright as the Sun compared to 6.73 × 10−13 times). For this to be true, Pleione must be much farther away from Earth than is ε Eridani. This is just what our results show: d = 118 pc for Pleione compared to d = 3.23 pc for ε Eridani.
EXAMPLE: The star δ (delta) Cephei, which lies 300 pc from Earth, is thousands of times more luminous than the Sun. Thanks to this great luminosity, stars like δ Cephei can be seen in galaxies millions of parsecs away. As an example, the Hubble Space Telescope has detected stars like δ Cephei within the galaxy NGC 3351, which lies in the direction of the constellation Leo. These stars appear only 9 × 10−10 as bright as δ Cephei. What is the distance to NGC 3351?
Situation: To determine the distance we want, we need to find the distance to a star within NGC 3351. We are told that certain stars within this galaxy have the same luminosity as δ Cephei but appear only 9 × 10−10 as bright.
Tools: We use the equation 
to relate two stars, one within NGC 3351 (call this star 1) and the identical star δ Cephei (star 2). Our goal is to find d1.
Answer: Since the two stars are identical, they have the same luminosity (L1 = L2, or L1/L2 = 1). The brightness ratio is b1/b2 = 9 × 10−10, so our equation tells us that
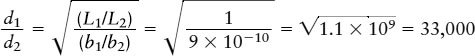
Hence, NGC 3351 is 33,000 times farther away than δ Cephei, which is 300 pc from Earth. The distance from Earth to NGC 3351 is therefore (33,000)(300 pc) = 107 pc, or 10 megaparsecs (10 Mpc).
Review: This example illustrates one technique that astronomers use to measure extremely large distances. We will learn more about stars like δ Cephei in Chapter 19, and in Chapter 23 we will explore further how they are used to determine the distances to remote galaxies.