BOX 17-4 TOOLS OF THE ASTRONOMER’S TRADE
Stellar Radii, Luminosities, and Surface Temperatures
Because stars emit light in almost exactly the same fashion as blackbodies, we can use the Stefan-Boltzmann law to relate a star’s luminosity (L), surface temperature (T), and radius (R). The relevant equation is
L = 4πR2σT4
As written, this equation involves the Stefan-Boltzmann constant σ, which is equal to 5.67 × 10−8 W m−2 K−4. In many calculations, it is more convenient to relate everything to the Sun, which is a typical star. Specifically, for the Sun we have L⊙ = 4πR⊙2σT⊙4, where L⊙ is the Sun’s luminosity, R⊙ is the Sun’s radius, and T⊙ is the Sun’s surface temperature (equal to 5800 K). Dividing the general equation for L by this specific equation for the Sun, we obtain
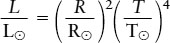
This formula is easier to use because the constant σ has cancelled out. We can also rearrange terms to arrive at a useful equation for the radius (R) of a star:
Radius of a star related to its luminosity and surface temperature
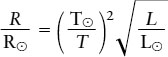

EXAMPLE: The bright reddish star Betelgeuse in the constellation Orion (see Figure 2-2) is 60,000 times more luminous than the Sun and has a surface temperature of 3500 K. What is its radius?
Situation: We are given the star’s luminosity L = 60,000 L⊙ and its surface temperature T = 3500 K. Our goal is to find the star’s radius R.
Tools: We use the above equation to find the ratio of the star’s radius to the radius of the Sun, R/R⊙. Note that we also know the Sun’s surface temperature, T⊙ = 5800 K.
Answer: Substituting these data into the above equation, we get
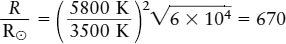
Review: Our result tells us that Betelgeuse’s radius is 670 times larger than that of the Sun. The Sun’s radius is 6.96 × 105 km, so we can also express the radius of Betelgeuse as (670)(6.96 × 105 km) = 4.7 × 108 km, which is more than 3 AU. If Betelgeuse were located at the center of our solar system, it would extend beyond the orbit of Mars!
EXAMPLE: Sirius, the brightest star in the sky, is actually two stars orbiting each other (a binary star). The less luminous star, Sirius B, is a white dwarf that is too dim to see with the naked eye. Its luminosity is 0.0025 L⊙ and its surface temperature is 10,000 K. How large is Sirius B compared to Earth?
Situation: Again we are asked to find a star’s radius from its luminosity and surface temperature.
Tools: We use the same equation as in the preceding example.
Answer: The ratio of the radius of Sirius B to the Sun’s radius is
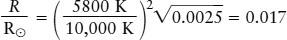
Since the Sun’s radius is R⊙ = 6.96 × 105 km, the radius of Sirius B is (0.017)(6.96 × 105 km) = 12,000 km. From Table 7-1, Earth’s radius (half its diameter) is 6378 km. Hence, this star is only about twice the radius of Earth.
Review: Sirius B’s radius would be large for a terrestrial planet, but it is minuscule for a star. The name dwarf is well deserved!
The radii of some stars have been measured with other techniques (see Section 17-11). These other methods yield values consistent with those calculated by the methods just described.