TOOLS OF THE ASTRONOMER’S TRADE

Using powers-of-ten notation makes it easy to multiply numbers. For example, suppose you want to multiply 100 by 1000. If you use ordinary notation, you have to write a lot of zeros:

By converting these numbers to powers-of-ten notation, we can write this same multiplication more compactly as

Because 2 + 3 = 5, we are led to the following general rule for multiplying numbers expressed in terms of powers of ten: Simply add the exponents.

EXAMPLE: 10⁴ × 10³ = 10⁴⁺³ = 10⁷.

To divide numbers expressed in terms of powers of ten, remember that 10⁻¹ = 1/10, 10⁻² = 1/100, and so on. The general rule for any exponent n is

In other words, dividing by 10ⁿ is the same as multiplying by 10⁻ⁿ. To carry out a division, you first transform it into multiplication by changing the sign of the exponent, and then carry out the multiplication by adding the exponents.

EXAMPLE: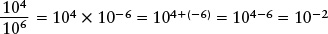

Usually a computation involves numbers like 3.0 × 10¹⁰, that is, an ordinary number multiplied by a factor of 10 with an exponent. In such cases, to perform multiplication or division, you can treat the numbers separately from the factors of 10ⁿ.

EXAMPLE: We can redo the first numerical example from Box 1-1 in a straightforward manner by using exponents: