BOX 1-3 TOOLS OF THE ASTRONOMER’S TRADE
Units of Length, Time, and Mass
To understand and appreciate the universe, we need to describe phenomena not only on the large scales of galaxies but also on the submicroscopic scale of the atom. Astronomers generally use units that are best suited to the topic at hand. For example, interstellar distances are conveniently expressed in either light-years or parsecs, whereas the diameters of the planets are more comfortably presented in kilometers.
Most scientists prefer to use a version of the metric system called the International System of Units, abbreviated SI (after the French name Système International). In SI units, length is measured in meters (m), time is measured in seconds (s), and mass (a measure of the amount of material in an object) is measured in kilograms (kg). How are these basic units related to other measures?
When discussing objects on a human scale, sizes and distances can also be expressed in millimeters (mm), centimeters (cm), and kilometers (km). These units of length are related to the meter as follows:
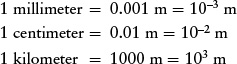
A useful set of conversions for the English system is

Each of these equalities can also be written as a fraction equal to 1. For example, you can write
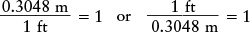
Fractions like this are useful for converting a quantity from one set of units to another. For example, the Saturn V rocket used to send astronauts to the Moon stands about 363 ft tall. How can we convert this height to meters? The trick is to remember that a quantity does not change if you multiply it by 1. Expressing the number 1 by the fraction (0.3048 m)/(1 ft), we can write the height of the rocket as

EXAMPLE: The diameter of Mars is 6794 km. Let’s try expressing this in miles.
CAUTION!
You can get into trouble if you are careless in applying the trick of taking the number whose units are to be converted and multiplying it by 1. For example, if we multiply the diameter by 1 expressed as (1.609 km)/(1 mi), we get
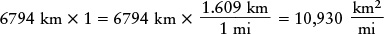
The unwanted units of km did not cancel, so this answer cannot be right. Furthermore, a mile is larger than a kilometer, so the diameter expressed in miles should be a smaller number than when expressed in kilometers.
The correct approach is to write the number 1 so that the unwanted units will cancel. The number we are starting with is in kilometers, so we must write the number 1 with kilometers in the denominator (“downstairs” in the fraction). Thus, we express 1 as (1 mi)/(1.609 km):

Now the units of km cancel as they should, and the distance in miles is a smaller number than in kilometers (as it must be).
When discussing very small distances such as the size of an atom, astronomers often use the micrometer (μm) or the nanometer (nm). These are related to the meter as follows:
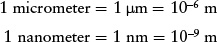
Thus, 1 μm = 103 nm. (Note that the micrometer is often called the micron.)
The basic unit of time is the second (s). It is related to other units of time as follows:

In the SI system, speed is properly measured in meters per second (m/s). Quite commonly, however, speed is also expressed in km/s and mi/h:
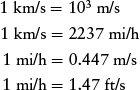
In addition to using kilograms, astronomers sometimes express mass in grams (g) and in solar masses (M⊙), where the subscript ⊙ is the symbol denoting the Sun. It is especially convenient to use solar masses when discussing the masses of stars and galaxies. These units are related to each other as follows:
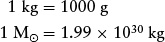
CAUTION!
You may be wondering why we have not given a conversion between kilograms and pounds (lb). The reason is that these units do not refer to the same physical quantity! A kilogram is a unit of mass, which is a measure of the amount of material in an object. By contrast, a pound is a unit of weight, which tells you how strongly gravity pulls on that object’s material. Consider a person who weighs 110 pounds on Earth, corresponding to a mass of 50 kg. Gravity is only about one-sixth as strong on the Moon as it is on Earth, so on the Moon this person would weigh only one-sixth of 110 pounds, or about 18 pounds. But that person’s mass of 50 kg is the same on the Moon; wherever you go in the universe, you take all of your material along with you. We will explore the relationship between mass and weight in Chapter 4.