TOOLS OF THE ASTRONOMER’S TRADE
Time Dilation and Length Contraction
The special theory of relativity describes how motion affects measurements of time and distance. By using the two basic principles of his theory—that no matter how fast you move, the laws of physics and the speed of light are the same—Einstein concluded that measurements of time and distance must depend on how the person making the measurements is moving.
To describe how measurements depend on motion, Einstein derived a series of equations named the Lorentz transformations, after the famous Dutch physicist Hendrik Antoon Lorentz. (Lorentz was a contemporary of Einstein who developed these equations independently but did not grasp their true meaning.) These equations tell us exactly how moving clocks slow down and how moving objects shrink.
To appreciate the Lorentz transformations, imagine two observers named Sergio and Majeeda. Sergio is at rest on Earth, while Majeeda is flying past in her spaceship at a speed v. Sergio and Majeeda both observe the same phenomenon on Earth—say, the beating of Sergio’s heart or the ticking of Sergio’s watch— which appears to occur over an interval of time. According to Sergio’s clock (which is not moving relative to the phenomenon), the phenomenon lasts for T0 seconds. This time period is called the proper time of the phenomenon. But according to Majeeda’s clock (which is moving relative to the phenomenon), the same phenomenon lasts for a different length of time, T seconds. These two time intervals are related as follows:
Lorentz transformation for time
T = time interval measured by an observer moving relative to the phenomenon
T0 = time interval measured by a observer not moving relative to the phenomenon (proper time)
v = speed of the moving observer relative to the phenomenon
c = speed of light
EXAMPLE: Sergio heats a cup of water in a microwave oven for 1 minute. According to Majeeda, who is flying past Sergio at 98% of the speed of light, how long does it take to heat the water?
Situation: The phenomenon in question is heating the water in the microwave oven. Sergio is not moving relative to this phenomenon (so he measures the proper time interval T0). Majeeda is moving at speed v = 0.98c relative to this phenomenon (so she measures a different time interval T). Our goal is to determine the value of T.
Tools: We use the Lorentz transformation for time to calculate T.
Answer: We have v/c 5 0.98, so
Review: A phenomenon that lasts for T0 = 1 minute on Sergio’s clock is stretched out to T = 5T0 = 5 minutes as measured on Majeeda’s clock moving at 98% of the speed of light. Other phenomena are affected in the same way: As measured by Majeeda, it takes 5 seconds for Sergio’s wristwatch to tick off one second, and the minute hand on Sergio’s wristwatch takes 5 hours to make a complete sweep. The converse is also true. As measured by Sergio, the minute hand on Majeeda’s wristwatch will take 5 hours to make a complete sweep. This phenomenon, in which events moving relative to an observer happen at a slower pace, is called time dilation.
The Lorentz transformation for time is plotted in Figure 21-2b, which shows how 1 second measured on a stationary clock (say, Sergio’s) is stretched out when measured using a clock carried by a moving observer (such as Majeeda). For speeds less than about half the speed of light, the mathematical factor 
is not too different from 1, and there is little difference between the recordings of the stationary and moving clocks. At the fastest speeds that humans have ever traveled (en route from Earth to the Moon), the difference between 1 and the factor is less than 10−9. So, for any speed associated with human activities, stationary and slowly moving clocks tick at essentially the same rate. As the next example shows, however, time dilation is important for subatomic particles that travel at speeds comparable to c.
EXAMPLE: When unstable particles called muons (pronounced “mew-ons”) are produced in experiments on Earth, they decay into other particles in an average time of 2.2 × 10−6 s. Muons are also produced by fast-moving protons from interstellar space when they collide with atoms in Earth’s upper atmosphere. These muons typically move at 99.9% of the speed of light and are formed at an altitude of 10 km. How long do such muons last before they decay?
Situation: The phenomenon in question is the life of a muon, which lasts a time T0 = 2.2 × 10−6 s as measured by an observer not moving with respect to the muon. Our goal is to find the time interval T measured by an observer on Earth, which is moving at v = 0.999c relative to the muon (the same speed at which the muon is moving relative to Earth).
607
Tools: As in the previous example, we use the Lorentz transformation for time.
Answer: Using v/c = 0.999,
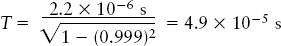
Review: At this speed, the muon’s lifetime is slowed down by time dilation by a factor of more than 22. Note that as measured by an observer on Earth, the time that it takes a muon produced at an altitude of 10 km = 10,000 m to reach Earth’s surface is
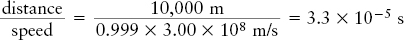
Were there no time dilation, such a muon would decay in just 2.2 × 10−6 s and would never reach Earth’s surface. But in fact, these muons are detected by experiments on Earth’s surface, because a muon moving at 0.999c lasts more than 3.3 × 10−5 s. The detection at Earth’s surface of muons from the upper atmosphere is compelling evidence for the reality of time dilation.
In the same terminology as “proper time,” we say that a ruler at rest measures proper length or proper distance (L0). According to the Lorentz transformations, distances perpendicular to the direction of motion are unaffected. However, a ruler of proper length L0 held parallel to the direction of motion shrinks to a length L, given by
Lorentz transformation for length
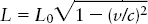
L = length of a moving object along the direction of motion
L0 = length of the same object at rest (proper length)
v = speed of the moving object
c = speed of light
EXAMPLE: Again, imagine that Majeeda is traveling at 98% of the speed of light relative to Sergio. If Majeeda holds a 1-m ruler parallel to the direction of motion, how long is this ruler as measured by Sergio?
Situation: The ruler is at rest relative to Majeeda, so she measures its proper length L0 = 1 m. Our goal is to determine its length L as measured by Sergio, who is moving at v = 0.98c relative to Majeeda and her ruler.
Tools: We use the Lorentz transformation for length.
Answer: With v/c = 0.98, we find
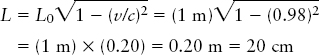
Review: We saw in the first example that according to Sergio, Majeeda’s clocks are ticking only one-fifth as fast as his. This example shows that he also measures Majeeda’s 1-m ruler to be only one-fifth as long (20 cm) when held parallel to the direction of motion. Note that the converse is also true: If Sergio holds a 1-m ruler parallel to the direction of relative motion, Majeeda measures it to be only 20 cm long. This shrinkage of length is called length contraction.
EXAMPLE: Consider again the above example about muons created 10 km above Earth’s surface. If a muon is traveling straight down, what is the distance to the surface as measured by an observer riding along with the muon?
Situation: Imagine a ruler that extends straight up from Earth’s surface to where the muon is formed. This ruler is at rest relative to Earth, so its length of 10 km is the proper length L0. Our goal is to find the length L of this ruler as measured by the observer riding with the muon.
Tools: As in the previous example, we use the Lorentz transformation for length.
Answer: With v/c = 0.999, we calculate
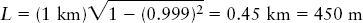
Review: The distance is contracted tremendously as measured by an observer riding with the muon. This result gives us another way to explain how such muons are able to reach Earth’s surface. As measured by the muon, the time required to travel the contracted distance is
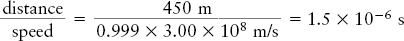
This time is less than the 2.2 × 10−6 s that an average muon takes to decay. Hence, muons can successfully reach Earth’s surface.