TOOLS OF THE ASTRONOMER’S TRADE

The Schwarzschild Radius

The Schwarzschild radius (R_Sch) is the distance from the center of a nonrotating black hole to its event horizon. You can think of this radius as the “size” of the black hole. For an object of a given mass, the Schwarzschild radius is the size that mass would need to be concentrated within, in order to make the escape speed from that object equal to the speed of light. The Schwarzschild radius is related to the mass M of the black hole by

Schwarzschild radius

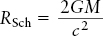
R_Sch = Schwarzschild radius of a black hole

G   = universal constant of gravitation

M   = mass of black hole

c    = speed of light

When using this formula, be careful to express the mass in kilograms, not solar masses, because of the units in which G and c are commonly expressed (G = 6.67 × 10⁻¹¹ N × m²/kg² and c = 3.00 × 10⁸ m/s). If you use M in kilograms, the answer that you get for R_Sch will be in meters.

EXAMPLE: Find the Schwarzschild radius (in kilometers) of a black hole with 10 times the mass of the Sun.

Situation: We are given the mass of the black hole (10 M_⊙) and wish to determine its Schwarzschild radius R_Sch.

Tools: We use the above formula for R_Sch, being careful to first convert the mass from solar masses to kilograms.

Answer: One solar mass is 1.99 × 10³⁰ kg, so in this case M = 10 × 1.99 × 10³⁰ kg = 1.99 × 10³¹ kg. The Schwarzschild radius of this black hole is then

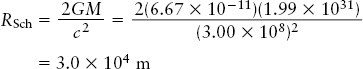
One kilometer is 10³ m, so the Schwarzschild radius of this 10-M_⊙ black hole is

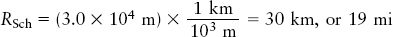
Review: The Schwarzschild radius is directly proportional to the mass of the black hole. Thus, a black hole with 10 times the mass (100 M_⊙) would have a Schwarzschild radius 10 times larger (R_Sch = 10 × 30 km = 300 km); a black hole with half the mass (5 M_⊙) would have half as large a Schwarzschild radius (R_Sch = 1/2 × 30 km = 15 km), and so on.