TOOLS OF THE ASTRONOMER’S TRADE

Estimating the Mass Inside the Sun’s Orbit

The force that keeps the Sun in orbit around the center of the Galaxy is the gravitational pull of all the matter interior to the Sun’s orbit—this force is described by Newton’s law of gravity. We can estimate the total mass of all of this matter using Newton’s form of Kepler’s third law (see Section 4-7 and Box 4-4):

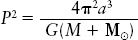
In this equation P is the orbital period of the Sun, a is the semimajor axis of the Sun’s orbit around the galactic center, G is the universal constant of gravitation, M is the amount of mass inside the Sun’s orbit, and M_⊙ is the mass of the Sun.

Because the Sun is only one of more than 10¹¹ stars in the Galaxy, the Sun’s mass is minuscule compared to M. Hence, we can safely replace the sum M + M_⊙ in the above equation with just M. If we now assume that the Sun’s orbit is a circle, the semimajor axis a of the orbit is just the radius of this circle, which we call r. The period P of the orbit is equal to 2πr/v, where v is the Sun’s orbital speed. You can then show that

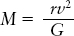
(We leave the derivation of this equation as an exercise at the end of this chapter.)

Now we can insert known values to obtain the mass inside the Sun’s orbit. Being careful to express distance in meters and speed in meters per second, we have v = 220 km/s = 2.2 × 10⁵ m/s, G = 6.67 × 10⁻¹¹ newton ∙ m²/kg², and

Hence, we find that

or, in terms of the mass of the Sun,

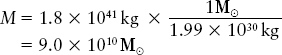
This estimate involves only mass that is interior to the Sun’s orbit. Matter outside the Sun’s orbit has no net gravitational effect on the Sun’s motion and thus does not enter into Kepler’s third law. (This is strictly true only if the matter outside our orbit is distributed over a sphere rather than a disk. In fact, the dark matter that dominates our Galaxy seems to have a spherical distribution.)