TOOLS OF THE ASTRONOMER’S TRADE

The Hubble Law, Redshifts, and Recessional Velocities

Suppose that you aim a telescope at a distant galaxy. The galaxy will be moving away from you in the Hubble flow. You take a spectrum of the galaxy and find that the spectral lines are shifted toward the red end of the spectrum. For example, a particular spectral line whose normal wavelength is λ₀ appears in the galaxy’s spectrum at a longer wavelength λ. The spectral line has thus been shifted by an amount Δλ = λ − λ₀. The redshift of the galaxy, z, is given by

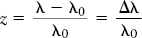
The redshift means that the galaxy is receding from us. According to the Hubble law, the recessional velocity v of a galaxy is related to its distance d from Earth by

where H₀ is the Hubble constant. We can rewrite this equation

Given the value of H₀, we can find the distance d to the galaxy if we know how to determine the recessional velocity v from the redshift z.

If the redshift is not too great (so that the redshift z is much less than 1), we can use the following Doppler shift equation to find the recessional speed:

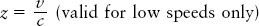
where c is the speed of light. For example, a 5% shift in wavelength (z = 0.05) corresponds to a recessional velocity of 5% of the speed of light (v = 0.05c).

For larger redshifts (around z = 1 or greater), a more complicated equation is needed to determine the recessional velocity. A small redshift can be explained by the Doppler shift as we have used here. However, as we will see in Chapter 25, larger redshifts arise from a large expansion of space and cannot be described as a simple Doppler shift. In fact, for galaxies at redshifts greater than about z > 1.5, recessional speeds exceed the speed of light. Due to the unique attributes of expanding space, faster-than-light recession is not a violation of Einstein’s laws.

EXAMPLE: When measured in a laboratory on Earth, the so-called K line of singly ionized calcium has a wavelength λ₀ = 393.3 nm. But when you observe the spectrum of the giant elliptical galaxy NGC 4889, you find this spectral line at λ = 401.8 nm. Using H₀ = 73 km/s/Mpc, find the distance to this galaxy.

Situation: We are given the values of λ and λ₀ for a line in this galaxy’s spectrum. Our goal is to determine the galaxy’s distance d.

Tools: We use the relationship z = (λ − λ₀)/λ₀ to determine the redshift. We then use the appropriate formula to determine the galaxy’s recessional velocity v, and finally use the Hubble law to determine the distance to the galaxy.

Answer: The redshift of this galaxy is

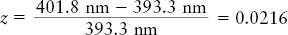
This value is substantially less than 0.1, so we can safely use the low-redshift relationship between recessional speed and redshift: v = zc. So NGC 4889 is moving away from us with a speed

Using H₀ = 73 km/s/Mpc in the Hubble law, the distance to this galaxy is

Review: This galaxy is receding from us at 0.0216 (2.16%) of the speed of light, and it is 89 megaparsecs (290 million light-years) away. Thus the light we see from NGC 4889 today left the galaxy 290 million years ago, even before the first dinosaurs appeared on Earth.