BOX 4-2 TOOLS OF THE ASTRONOMER’S TRADE
Using Kepler’s Third Law
Kepler’s third law relates the sidereal period P of an object orbiting the Sun to the semimajor axis a of its orbit:
P2 = a3
You must keep two essential points in mind when working with this equation:
- The period P must be measured in years, and the semimajor axis a must be measured in astronomical units (AU). Otherwise you will get nonsensical results.
- This equation applies only to the special case of an object, like a planet, that orbits the Sun. If you want to analyze the orbit of the Moon around Earth, of a spacecraft around Mars, or of a planet around a distant star, you must use a different, generalized form of Kepler’s third law. We discuss this alternative equation in Section 4-7 and Box 4-4.
EXAMPLE: The average distance from Venus to the Sun is 0.72 AU. Use this to determine the sidereal period of Venus.
Situation: The average distance from Venus to the Sun is the semimajor axis a of the planet’s orbit. Our goal is to calculate the planet’s sidereal period P.
Tools: To relate a and P we use Kepler’s third law, P2 = a3.
Answer: We first cube the semimajor axis (multiply it by itself twice):
a3 = (0.72)3 = 0.72 × 0.72 × 0.72 = 0.373
According to Kepler’s third law this is also equal to P2, the square of the sidereal period. So, to find P, we have to “undo” the square, that is, take the square root. Using a calculator, we find
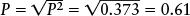
Review: The sidereal period of Venus is 0.61 years, or a bit more than seven Earth months. This result makes sense: A planet with a smaller orbit than Earth’s (an inferior planet) must have a shorter sidereal period than Earth.
EXAMPLE: A certain small asteroid (a rocky body a few tens of kilometers across) takes eight years to complete one orbit around the Sun. Find the semimajor axis of the asteroid’s orbit.
Situation: We are given the sidereal period P = 8 years, and are to determine the semimajor axis a.
Tools: As in the preceding example, we relate a and P using Kepler’s third law, P2 = a3.
Answer: We first square the period:
P2 = 82 = 8 × 8 = 64
From Kepler’s third law, 64 is also equal to a3. To determine a, we must take the cube root of a3, that is, find the number whose cube is 64. If your calculator has a cube root function, denoted by the symbol 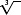 , you can use it to find that the cube root of 64 is 4:
, you can use it to find that the cube root of 64 is 4:  = 4. Otherwise, you can determine by trial and error that the cube of 4 is 64:
= 4. Otherwise, you can determine by trial and error that the cube of 4 is 64:
43 = 4 × 4 × 4 = 64
Because the cube of 4 is 64, it follows that the cube root of 64 is 4 (taking the cube root “undoes” the cube).
With either technique you find that the orbit of this asteroid has semimajor axis a = 4 AU.
Review: The period is greater than 1 year, so the semimajor axis is greater than 1 AU. Note that a = 4 AU is intermediate between the orbits of Mars and Jupiter (see Table 4-3). Many asteroids are known with semimajor axes in this range, forming a region in the solar system called the asteroid belt.