TOOLS OF THE ASTRONOMER’S TRADE

Kepler’s original statement of his third law, P² = a³, is valid only for objects that orbit the Sun. (Box 4-2 shows how to use this equation.) But Newton’s form of Kepler’s third law is much more general: It can be used in any situation where two objects of masses m₁ and m₂ orbit each other. For example, Newton’s form is the equation to use for a moon orbiting a planet or a satellite orbiting Earth. This equation is

Newton’s form of Kepler’s third law:

Notice that P, a, m¹, and m² must be expressed in these particular units. If you fail to use the correct units, your answer will be incorrect.

EXAMPLE: Io (pronounced “eye-oh”) is one of the four large moons of Jupiter discovered by Galileo and shown in Figure 4-16. It orbits at a distance of 421,600 km from the center of Jupiter and has an orbital period of 1.77 days. Determine the combined mass of Jupiter and Io.

Situation: We are given Io’s orbital period P and semimajor axis a (the distance from Io to the center of its circular orbit, which is at the center of Jupiter). Our goal is to find the sum of the masses of Jupiter (m₁) and Io (m₂).

Tools: Because this orbit is not around the Sun, we must use Newton’s form of Kepler’s third law to relate P and a. This relationship also involves m₁ and m₂, whose sum (m₁ + m₂) we are asked to find.

Answer: To solve for m₁ + m₂, we rewrite the equation in the form

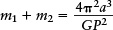
To use this equation, we have to convert the distance a from kilometers to meters and convert the period P from days to seconds. There are 1000 meters in 1 kilometer and 86,400 seconds in 1 day, so

We can now put these values and the value of G into the above equation:

Review: Io is very much smaller than Jupiter, so its mass is only a small fraction of the mass of Jupiter. Thus, m₁ + m₂ is very nearly the mass of Jupiter alone. We conclude that Jupiter has a mass of 1.90 × 10²⁷ kg, or about 300 times the mass of Earth. This technique can be used to determine the mass of any object that has a second, much smaller object orbiting it. Astronomers use this technique to find the masses of stars, black holes, and entire galaxies of stars.