TOOLS OF THE ASTRONOMER’S TRADE

The Sun and stars behave like nearly perfect blackbodies. Wien’s law and the Stefan-Boltzmann law can therefore be used to relate the surface temperature of the Sun or a distant star to the energy flux and wavelength of maximum emission of its radiation. The following examples show how to do this.

EXAMPLE: The maximum intensity of sunlight is at a wavelength of roughly 500 nm = 5.0 × 10⁻⁷ m. Use this information to determine the surface temperature of the Sun

Situation: We are given the Sun’s wavelength of maximum emission λ_max, and our goal is to find the Sun’s surface temperature, denoted by T_⊙. (The symbol ⊙ is the standard astronomical symbol for the Sun.)

Tools: We use Wien’s law to relate the values of λ_max and T_⊙.

Answer: As written, Wien’s law tells how to find λ_max if we know the surface temperature. To find the surface temperature from λ_max, we first rearrange the formula, then substitute the value of λ_max:

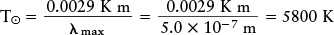
Review: This temperature is very high by Earth standards, about the same as an iron-welding arc.

EXAMPLE: Using detectors above Earth’s atmosphere, astronomers have measured the average flux of solar energy arriving at Earth. This value, called the solar constant, is equal to 1370 W m⁻². Use this information to calculate the Sun’s surface temperature. (This calculation provides a check on our result from the preceding example.)

Situation: The solar constant is the flux of sunlight as measured at Earth. We want to use the value of the solar constant to calculate T_⊙.

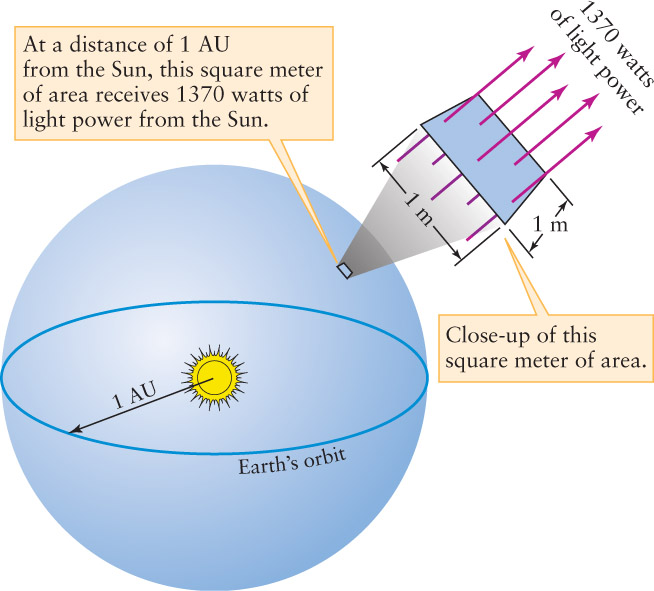
Tools: It may seem that all we need is the Stefan-Boltzmann law, which relates flux to surface temperature. However, the quantity F in this law refers to the flux measured at the Sun’s surface, not at Earth. Hence, we will first need to calculate F from the given information.

Answer: To determine the value of F, we first imagine a huge sphere of radius 1 AU with the Sun at its center, as shown in the figure. Each square meter of that sphere receives 1370 watts of power from the Sun, so the total energy radiated by the Sun per second is equal to the solar constant multiplied by the sphere’s surface area. The result, called the luminosity of the Sun and denoted by the symbol L_⊙, is L_⊙ = 3.90 × 10²⁶ W. That is, in 1 second the Sun radiates 3.90 × 10²⁶ joules of energy into space. Because we know the size of the Sun, we can compute the energy flux (energy emitted per square meter per second) at its surface. The radius of the Sun is R_⊙ = 6.96 × 10⁸ m, and the Sun’s surface area is 4πR_⊙². Therefore, its energy flux F_⊙ is the Sun’s luminosity (total energy emitted by the Sun per second) divided by the Sun’s surface area (the number of square meters of surface):

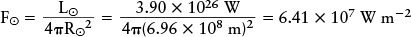
Once we have the Sun’s energy flux F_⊙ we can use the Stefan-Boltzmann law to find the Sun’s surface temperature T_⊙:

Taking the fourth root (the square root of the square root) of this value, we find the surface temperature of the Sun to be T_⊙ = 5800 K.

Review: Our result for T_⊙ agrees with the value we computed in the previous example using Wien’s law. Notice that the solar constant of 1370 W m⁻² is very much less than F_⊙ the flux at the Sun’s surface. By the time the Sun’s radiation reaches Earth, it is spread over a greatly increased area.

EXAMPLE: Sirius, the brightest star in the night sky, has a surface temperature of about 10,000 K. Find the wavelength at which Sirius emits most intensely.

Situation: Our goal is to calculate the wavelength of maximum emission of Sirius (λ_max) from its surface temperature T.

Tools: We use Wien’s law to relate the values of λ_max and T.

Answer: Using Wien’s law,

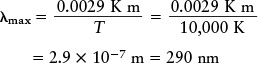
Review: Our result shows that Sirius emits light most intensely in the ultraviolet. In the visible part of the spectrum, it emits more blue light than red light (like the curve for 12,000 K in Figure 5-11), so Sirius has a distinct blue color.

EXAMPLE: How does the energy flux from Sirius compare to the Sun’s energy flux?

Situation: To compare the energy fluxes from the two stars, we want to find the ratio of the flux from Sirius to the flux from the Sun.

Tools: We use the Stefan-Boltzmann law to find the flux from Sirius and from the Sun, which from the preceding examples have surface temperatures 10,000 K and 5800 K, respectively.

Answer: For the Sun, the Stefan-Boltzmann law is F_⊙ = σT_⊙⁴, and for Sirius we can likewise write F_* = σT_*⁴, where the subscripts ⊙ and * refer to the Sun and Sirius, respectively. If we divide one equation by the other to find the ratio of fluxes, the Stefan-Boltzmann constants cancel out and we get

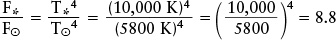
Review: Because Sirius has such a high surface temperature, each square meter of its surface emits 8.8 times more energy per second than a square meter of the Sun’s relatively cool surface. Sirius is actually a larger star than the Sun, so it has more square meters of surface area and, hence, its total energy output is more than 8.8 times that of the Sun.