TOOLS OF THE ASTRONOMER’S TRADE

Magnification and Light-Gathering Power

The magnification of a telescope is equal to the focal length of the objective divided by the focal length of the eyepiece. Telescopic eyepieces are usually interchangeable, so the magnification of a telescope can be changed by using eyepieces of different focal lengths.

EXAMPLE: A small refracting telescope has an objective of focal length 120 cm. If the eyepiece has a focal length of 4.0 cm, what is the magnification of the telescope?

Situation: We are given the focal lengths of the telescope’s objective and eyepiece lenses. Our goal is to calculate the magnification provided by this combination of lenses.

Tools: We use the relationship that the magnification equals the focal length of the objective (120 cm) divided by the focal length of the eyepiece (4.0 cm).

Answer: Using this relationship,

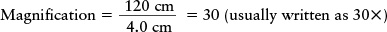
Review: A magnification of 303 means that as viewed through this telescope, a large lunar crater that subtends an angle of 1 arcminute to the naked eye will appear to subtend an angle 30 times greater, or 30 arcminutes (one-half of a degree). This magnification makes the details of the crater much easier to see.

If a 2.0-cm-focal-length eyepiece is used instead, the magnification will be (120 cm)/(2.0 cm) = 60×. The shorter the focal length of the eyepiece, the greater the magnification.

The light-gathering power of a telescope depends on the diameter of the objective lens; it does not depend on the focal length. The light-gathering power is proportional to the square of the diameter. As an example, a fully dark adapted human eye has a pupil diameter of about 5 mm. By comparison, a small telescope whose objective lens is 5 cm in diameter has 10 times the diameter and 10² = 100 times the light-gathering power of the eye. (Recall that there are 10 mm in 1 cm.) Hence, this telescope allows you to see objects 100 times fainter than you can see without a telescope.

EXAMPLE: The same relationships apply to reflecting telescopes, discussed in Section 6-2. Each of the two Keck telescopes on Mauna Kea in Hawaii (discussed in Section 6-3; see Figure 6-16) uses a concave mirror 10 m in diameter to bring starlight to a focus. How many times greater is the light-gathering power of either Keck telescope compared to that of the human eye?

Situation: We are given the diameters of the pupil of the human eye (5 mm) and of the mirror of either Keck telescope (10 m). Our goal is to compare the light-gathering powers of these two optical instruments.

Tools: We use the relationship that light-gathering power is proportional to the square of the diameter of the area that gathers light. Hence, the ratio of the light-gathering powers is equal to the square of the ratio of the diameters.

Answer: We first calculate the ratio of the diameter of the Keck mirror to the diameter of the pupil. To determine this ratio, we must first express both diameters in the same units. Because there are 1000 mm in 1 meter, the diameter of the Keck mirror can be expressed as

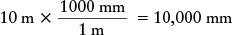
Thus, the light-gathering power of either of the Keck telescopes is greater than that of the human eye by a factor of

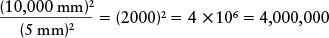
Review: Either Keck telescope can gather 4 million times as much light as a human eye. When it comes to light-gathering power, the bigger the telescope, the better!