1-5 Astronomers use angles to denote the positions and apparent sizes of objects in the sky
Whether they study planets, stars, galaxies, or the very origins of the universe, astronomers must know where to point their telescopes. For this reason, an important part of astronomy is keeping track of the positions of objects in the sky. A system for measuring angles is an essential part of this aspect of astronomy (Figure 1-11).
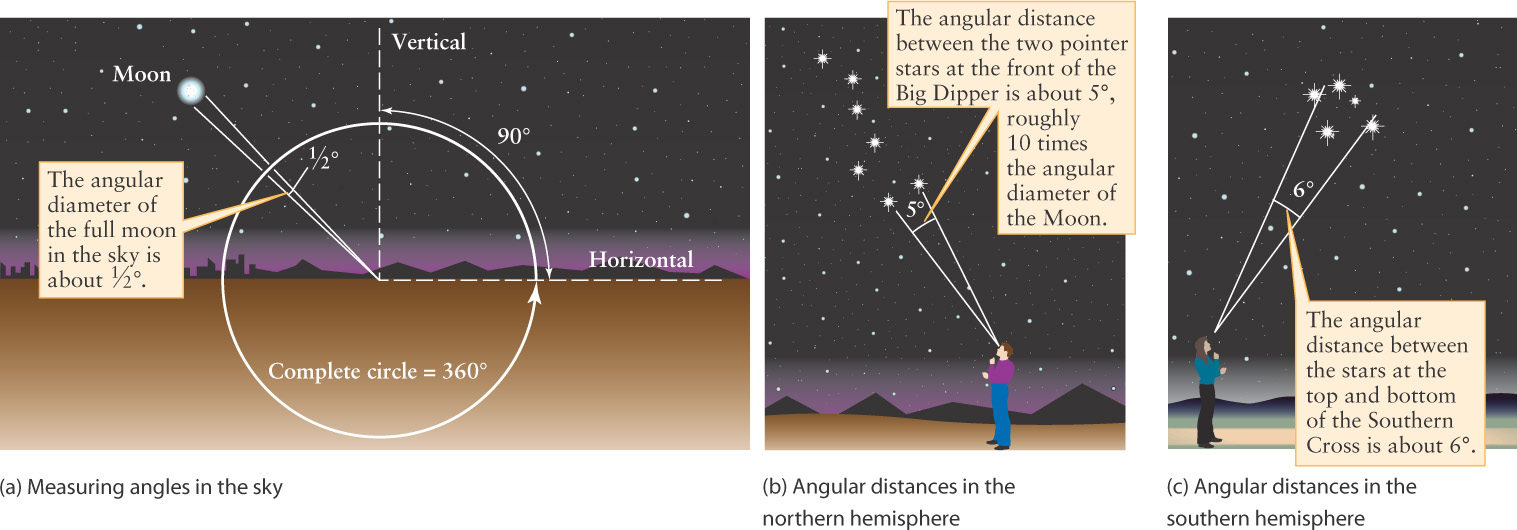
Angles are a tool that we will use throughout our study of astronomy
An angle measures the opening between two lines that meet at a point. A basic unit to express angles is the degree, designated by the symbol °. A full circle is divided into 360°, and a right angle measures 90° (Figure 1-11a). As Figure 1-11b shows, if you draw lines from your eye to each of the two “pointer stars” in the Big Dipper, the angle between these lines—that is, the angular distance between these two stars—is about 5°. (In Chapter 2 we will see that these two stars “point” to Polaris, the North Star.) The angular distance between the stars that make up the top and bottom of the Southern Cross, which is visible from south of the equator, is about 6° (Figure 1-11c).
Astronomers also use angles to describe the apparent size of a celestial object—that is, how wide the object appears in the sky. For example, the angle covered by the diameter of the full moon is about ½° (Figure 1-11a). We therefore say that the angular diameter (or angular size) of the Moon is ½°. Alternatively, astronomers say that the Moon subtends, or extends over, an angle of ½°. Ten full moons could fit side by side between the two pointer stars in the Big Dipper.
The average adult human hand held at arm’s length provides a means of estimating angles, as Figure 1-12 shows. For example, a fist covers an angle of about 10°, whereas a fingertip is about 1° wide. You can use various segments of your index finger extended to arm’s length to estimate angles a few degrees across.

To talk about smaller angles, we subdivide the degree into 60 arcminutes (also called minutes of arc), which is commonly abbreviated as 60 arcmin or 60'. An arcminute is further subdivided into 60 arcseconds (or seconds of arc), usually written as 60 arcsec or 60?. Thus,
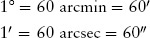
For example, on January 1, 2007, the planet Saturn had an angular diameter of 19.6 arcsec as viewed from Earth. That is a convenient, precise statement of how big the planet appeared in Earth’s sky on that date. (Because this angular diameter is so small, to the naked eye Saturn appears simply as a point of light. To see any detail on Saturn, such as the planet’s rings, requires a telescope.)
If we know the angular size of an object as well as the distance to that object, we can determine the actual linear size of the object (measured in kilometers or miles, for example). Box 1-1 describes how this is done.
CONCEPT CHECK 1-3
Is it possible for a basketball to look bigger than the Moon? Smaller?
Yes. The apparent size of an object is given by how wide it appears (in other words, the angle that it subtends). By moving a basketball near and far, it can appear very large or very small.