2-8 Astronomical observations led to the development of the modern calendar
Our calendar is complex because a year does not contain a whole number of days
Just as the day is a natural unit of time based on Earth’s rotation, the year is a natural unit of time based on Earth’s revolution about the Sun. However, nature has not arranged things for our convenience. The year does not divide into exactly 365 whole days. Ancient astronomers realized that the length of a year is approximately 365¼ days, motivating the Roman emperor Julius Caesar to establish the system of “leap years” to account for this extra quarter of a day. By adding an extra day to the calendar every four years, he hoped to ensure that seasonal astronomical events, such as the beginning of spring, would occur on the same date year after year.
BOX 2-2 TOOLS OF THE ASTRONOMER’S TRADE
Sidereal Time
 If you want to observe a particular object in the heavens, the ideal time to do so is when the object is high in the sky, on or close to the upper meridian.
If you want to observe a particular object in the heavens, the ideal time to do so is when the object is high in the sky, on or close to the upper meridian.
Timing observations to occur when an object is high in the sky minimizes the distorting effects of Earth’s atmosphere, which increase as you view objects closer to the horizon. For astronomers who study the Sun, this means making observations at local noon, which is not too different from noon as determined using mean solar time. For astronomers who observe planets, stars, or galaxies, however, the optimum time to observe depends on the particular object to be studied. Given the location of a given object on the celestial sphere, when will that object be on the upper meridian?
To answer this question, astronomers use sidereal time rather than solar time. It is different from the time on your wristwatch. In fact, a sidereal clock and an ordinary clock even tick at different rates, because they are based on different astronomical objects. Ordinary clocks are related to the position of the Sun, while sidereal clocks are based on the position of the vernal equinox, the location from which right ascension is measured. (See Box 2-1 for a discussion of right ascension.)
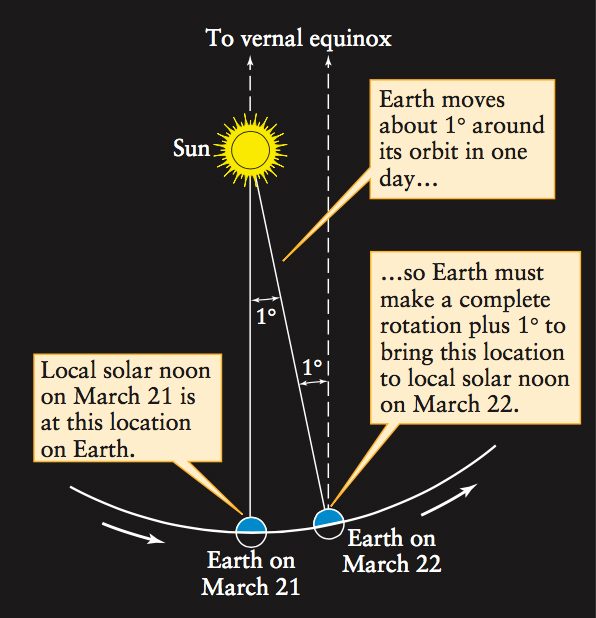
 Regardless of where the Sun is, midnight sidereal time at your location is defined to be when the vernal equinox crosses your upper meridian. (Like solar time, sidereal time depends on where you are on Earth.) A sidereal day is the time between two successive upper meridian passages of the vernal equinox. By contrast, an apparent solar day is the time between two successive upper meridian crossings of the Sun. The illustration shows why these two kinds of day are not equal. Because Earth orbits the Sun, Earth must make one complete rotation plus about 1° to get from one local solar noon to the next. This extra 1° of rotation corresponds to 4 minutes of time, which is the amount by which a solar day exceeds a sidereal day. To be precise:
Regardless of where the Sun is, midnight sidereal time at your location is defined to be when the vernal equinox crosses your upper meridian. (Like solar time, sidereal time depends on where you are on Earth.) A sidereal day is the time between two successive upper meridian passages of the vernal equinox. By contrast, an apparent solar day is the time between two successive upper meridian crossings of the Sun. The illustration shows why these two kinds of day are not equal. Because Earth orbits the Sun, Earth must make one complete rotation plus about 1° to get from one local solar noon to the next. This extra 1° of rotation corresponds to 4 minutes of time, which is the amount by which a solar day exceeds a sidereal day. To be precise:
1 sidereal day = 23h 56m 4.091s
where the hours, minutes, and seconds are in mean solar time.
One day according to your wristwatch is one mean solar day, which is exactly 24 hours of solar time long. A sidereal clock measures sidereal time in terms of sidereal hours, minutes, and seconds, where one sidereal day is divided into 24 sidereal hours.
This explains why a sidereal clock ticks at a slightly different rate than your wristwatch. As a result, at some times of the year a sidereal clock will show a very different time than an ordinary clock. (At local noon on March 21, when the Sun is at the vernal equinox, a sidereal clock will say that it is midnight. Do you see why?)
We can now answer the question in the opening paragraph. The vernal equinox, whose celestial coordinates are R.A. = 0h 0m 0s, Decl. = 0° 0' 0?, crosses the upper meridian at midnight sidereal time (0:00). The autumnal equinox, which is on the opposite side of the celestial sphere at R.A. = 12h 0m 0s, Decl. = 0° 0' 0?, crosses the upper meridian 12 sidereal hours later at noon sidereal time (12:00). As these examples illustrate, any object crosses the upper meridian when the sidereal time is equal to the object’s right ascension. That is why astronomers measure right ascension in units of time rather than degrees, and why right ascension is always given in sidereal hours, minutes, and seconds.
EXAMPLE: Suppose you want to observe the bright star Spica (Figure 2-6), which has epoch 2000 coordinates R.A. = 13h 25m 11.6s, Decl. = -11° 9' 41?. What is the best time to do this?
Situation: Our goal is to find the time when Spica passes through your upper meridian, where it can best be observed.
Tools: We use the idea that a celestial object is on your upper meridian when the sidereal time equals the object’s right ascension.
Answer: Based on the given right ascension of Spica, it will be best placed for observation when the sidereal time at your location is about 13:25. (Note that sidereal time is measured using a 24-hour clock.)
Review: By itself, our answer doesn’t tell you what time on your wristwatch (which measures mean solar time) is best for observing Spica. That’s why most observatories are equipped with a sidereal clock.
While sidereal time is extremely useful in astronomy, mean solar time is still the best method of timekeeping for most earthbound purposes. All time measurements in this book are expressed in mean solar time unless otherwise stated.
Caesar’s system would have been perfect if the year were exactly 365¼ days long and if there were no precession. Unfortunately, this is not the case. To be more accurate, astronomers now use several different types of years. For example, the sidereal year is defined to be the time required for the Sun to return to the same position with respect to the stars. It is equal to 365.2564 mean solar days, or 365d 6h 9m 10s.
The sidereal year is the orbital period of Earth around the Sun, but it is not the year on which we base our calendar. Like Caesar, most people want annual events—in particular, the first days of the seasons—to fall on the same date each year. For example, we want the first day of spring to occur on March 21. But spring begins when the Sun is at the vernal equinox, and the vernal equinox moves slowly against the background stars because of precession. Therefore, to set up a calendar we use the tropical year, which is equal to the time needed for the Sun to return to the vernal equinox. This period is equal to 365.2422 mean solar days, or 365d 5h 48m 46s. Because of precession, the tropical year is 20 minutes and 24 seconds shorter than the sidereal year.
Caesar’s assumption that the tropical year equals 365¼ days was off by 11 minutes and 14 seconds. This tiny error adds up to about three days every four centuries. Although Caesar’s astronomical advisers were aware of the discrepancy, they felt that it was too small to matter. However, by the sixteenth century the first day of spring was occurring on March 11.
The Roman Catholic Church became concerned because Easter kept shifting to progressively earlier dates. To straighten things out, Pope Gregory XIII instituted a calendar reform in 1582. He began by dropping 10 days (October 4, 1582, was followed by October 15, 1582), which brought the first day of spring back to March 21. Next, he modified Caesar’s system of leap years.
Caesar had added February 29 to every calendar year that is evenly divisible by four. Thus, for example, 2008, 2012, and 2016 are all leap years with 366 days. But we have seen that this system produces an error of about three days every four centuries. To solve the problem, Pope Gregory decreed that only the century years evenly divisible by 400 should be leap years. For example, the years 1700, 1800, and 1900 (which would have been leap years according to Caesar) were not leap years in the improved Gregorian system, but the year 2000, which can be divided evenly by 400, was a leap year.
We use the Gregorian system today. It assumes that the year is 365.2425 mean solar days long, which is very close to the true length of the tropical year. In fact, the error is only one day in every 3300 years, which won’t cause any problems for a long time.