Answers

ConceptChecks

ConceptCheck 4-1: When a planet is moving retrograde, the planet can be observed night after night to be slowly drifting from east to west compared to the very distant background stars (Figure 4-2). This is opposite to how a planet typically appears to move. However, regardless of this slow movement, all objects always appear to rise in the east and set in the west on a daily basis due to Earth’s rotation.

ConceptCheck 4-2: The Greeks’ ancient geocentric model used a nonspinning, stationary Earth where the stars, planets, and the Sun all moved around Earth.

ConceptCheck 4-3: In the Ptolemaic model, the planets are continuously orbiting in circles such that they appear to move backward for a brief time. However, the planets never actually stop and change their directions (Figure 4-3).

ConceptCheck 4-4: No. A planet only appears to move in retrograde motion if seen from another planet if the two planets move at different speeds and pass one another (Figure 4-5). An imaginary observer on the stationary Sun would only see planets moving in the same direction as they orbit the Sun.

ConceptCheck 4-5: Mars has an orbit around the Sun that is larger than Earth’s orbit. As a result, Mars never moves to a position between Earth and the Sun, so Mars never is at inferior conjunction (Figure 4-6).

ConceptCheck 4-6: In Copernicus’s heliocentric model, the more distant planets are moving slower than the planets closer to the Sun. As a faster-moving Earth moves past a slower-moving Mars, there is a brief time in which Mars appears to move backward through the sky. However, the planets never actually reverse their directions.

ConceptCheck 4-7: Slowly moving Jupiter does not move very far along its orbit in the length of time it takes for Earth to pass by Jupiter, move around the Sun, and pass by Jupiter again, giving Jupiter a synodic period similar to Earth’s orbital period around the Sun. However, slow-moving Jupiter takes more than a decade to move around the Sun back to its original starting place as measured by the background stars, giving it a large sidereal period.

ConceptCheck 4-8: Initially, Copernicus’s model was no more accurate at predicting the positions and motions of the planets than Ptolemy’s model. However, Copernicus’s model turned out to be more closely related to the actual motions of the planets around the Sun than was Ptolemy’s model of planets orbiting Earth. With subsequent measurements, Ptolemy’s model was proven wrong.

ConceptCheck 4-9: An ellipse with an eccentricity of zero is a perfect circle (see Figure 4-10b) and, compared to Mars’s e = 0.093, the eccentricity of Venus’ orbit is e = 0.007. Venus has a smaller eccentricity so its orbit is closer to a perfect circle in shape.

ConceptCheck 4-10: Kepler’s second law says that objects are moving slowest when they are farthest from the object they are orbiting, so an Earth-orbiting satellite will move slowest when it is farthest from Earth. Just as the Sun is at one focus for a planet’s elliptical orbit, Earth is at one focus for a satellite’s elliptical orbit (Figure 4-11).

ConceptCheck 4-11: According to Kepler’s third law, planets closer to the Sun move faster than planets farther from the Sun. For objects orbiting Earth, the object closer to Earth is also moving the fastest, which, in this case, is the space shuttle.

ConceptCheck 4-12: No. Kepler’s laws of planetary motion apply to any objects in space that orbit around another object, including comets orbiting the Sun, man-made satellites and moons orbiting planets, and even stars orbiting other stars.

ConceptCheck 4-13: When Venus is on the opposite side of the Sun from Earth, it will be in a full or gibbous phase. The full phase can occasionally be observed because Earth and Venus do not orbit the Sun in the same exact plane.

ConceptCheck 4-14: Galileo was the first person to use and widely share what he learned from his telescope observations, and a telescope is necessary in order to observe Jupiter’s tiny moons.

ConceptCheck 4-15: According to Newton’s first law, the rock will continue to travel in the same direction, and with the same speed, as long as there is no net outside force. Note that this principle applies no matter how massive the rock is, or how fast it’s traveling.

ConceptCheck 4-16: As described by Newton’s third law, the forces the sumo wrestlers exert on each other are of equal strength, but in opposite directions. This is true even though they are different in size and even though one wrestler is pushed out of the ring. Frictional forces from the floor and their body masses influence which wrestler moves the most, but the forces they exert onto each other are of equal strength.

ConceptCheck 4-17: Expressing Newton’s second law in terms of acceleration, the acceleration of an object is given by a = F/m. Since the gravitational forces on the diver and Earth are of equal strength, the smaller mass—the diver—will have the larger acceleration. Because Earth is so much more massive than the diver, Earth’s acceleration in this case is nowhere near measurable.

ConceptCheck 4-18: According to Newton’s universal law of gravitation, the gravitational attraction between two objects depends on the square of the distance between them. In this case, if the asteroids drift 3 times closer together, then the gravitational force of attraction between them increases 3² times, or, in other words, becomes 9 times greater.

ConceptCheck 4-19: At the cannonball’s highest point, it is momentarily at rest and has gravitational potential energy, but no kinetic energy. Starting from the chemical energy in gunpowder, that chemical energy is transferred to the cannonball, giving it kinetic energy. As the ball rises, kinetic energy is transformed into gravitational potential energy until the ball reaches its peak.

ConceptCheck 4-20: Air drag removes orbital energy and could put the spacecraft on the elliptical path D. Firing the rocket thruster adds orbital energy and could put the spacecraft on the elliptical path F. A circular orbit requires special parameters, so it is not surprising that most moons and planets have at least slightly elliptical orbits.

ConceptCheck 4-21: In order for an object to feel air drag, it must pass through the air. Since Earth and our air orbit the Sun together, Earth feels no air drag and we can orbit the Sun indefinitely.

ConceptCheck 4-22: An object’s escape speed from a planet does not depend on the object’s mass, so both rocks can be shot at the same speed, which is the escape speed from the Moon. As illustrated in Figure 4-20, for two objects with the same speed, the more massive object has more kinetic energy, so the kinetic energy of the two rocks will not be equal, and more energy is required to shoot the larger rock off of the Moon.

ConceptCheck 4-23: Yes. The escape speed 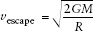depends on both the mass and radius of the planet. If another Earth-mass planet had a larger radius (which is certainly possible), its escape speed would be less than that of Earth.

ConceptCheck 4-24: The object—on its high-energy hyperbolic orbit—would have to lose orbital energy in order to enter a lower-energy elliptical or circular orbit as a moon. Special circumstances are required to lose this much energy, which is why we do not think Earth simply captured our Moon as it passed by.

CalculationChecks

CalculationCheck 4-1: According to Kepler’s third law, P² = a³. So, if P² = (39.5)³, then P = 39.5^3/2 = 248 years.

CalculationCheck 4-2: Using Newton’s universal law of gravitation, F_{Mars-astronaut} = G(m_Mars) × (m_astronaut) ÷ (radius)² = 6.67 × 10⁻¹¹ × 6.4 × 10²³ × 75 ÷ (3.4 × 10⁶)² = 277 newtons, which we can convert to pounds because 277 newtons × 0.255 lbs/N = 76 pounds.