- Step 1
- Step 2
- Step 3
- Step 4
- Step 5
- Step 6
- Step 7
- Step 8
- Step 9
- Step 10
Chapter 2. Chapter 2: Using Punnett Squares and Probability to Analyze a Pedigree
Introduction
A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
Draw the pedigree as described using the standard pedigree symbols provided by dragging them to the correct places. Remember that the trait is rare and thus people coming into the pedigree are not considered carriers or affected unless there is evidence to the contrary.
Symbols are as follows:
An empty square is an unaffected male.
An empty circle is an unaffected female.
Shaded or marked symbols represent an individual affected by the trait.
| A. |
| B. |












































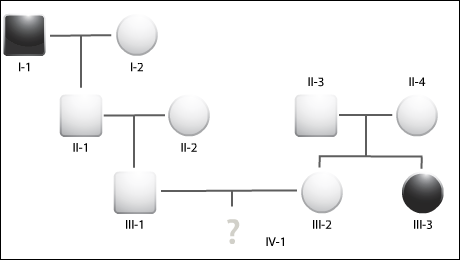
The paternal grandmother of the man and the man himself do not have galactosemia, so their symbols would be
The paternal grandmother does not carry alleles for galactosemia. How many disease alleles at most could the father of the man have inherited from that grandfather and grandmother?
Could the father of the man, having inherited at most one allele for galactosemia, been affected by the disease?
A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the apparent mode of inheritance in this pedigree?
| A. |
| B. |
| C. |
| D. |
The trait appears in every generation.
Two unaffected individuals can have an affected child.
One gender is affected more so than another.
A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the genotype of the man's father (II-1)?
| A. |
| B. |
| C. |
| D. |
If one parent is AA, the child can still be aa.
A_ means that the father could be either AA or Aa.
Aa individuals are affected.

A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the genotype of the man (III-1)?
| A. |
| B. |
| C. |
| D. |
The man could be AA or Aa.
A_ individuals are affected.
Individuals can be aa and be unaffected.

A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the probability of the man (III-1) carrying the recessive allele for galactosemia?
| A. |
| B. |
| C. |
| D. |
What do you know about the man's father?
Is it necessary to know the genotype of the mother to answer this question?
Can you safely assume he is not aa?

A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the genotype of the man's wife (III-2)?
| A. |
| B. |
| C. |
| D. |
How can you tell if his wife is AA versus Aa?
What does being unaffected tell you about her possible genotypes?

A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the probability of the man's wife carrying the recessive allele for galactosemia?
| A. |
| B. |
| C. |
| D. |
Since you know she cannot be aa, the probability of her being a carrier is determined by ____.
Because her parents are unaffected but her sister is affected, you know that the cross of her parents would have been _____.

A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the combined probability of both the man and his wife being carriers of the galactosemia allele?
| A. |
| B. |
| C. |
| D. |
When looking at the chance of two or more events occurring together, you would use the addition rule.
When looking at the chance of at least one of the parents being a carrier, you would use the addition rule.

A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
What is the probability their first child has galactosemia?
| A. |
| B. |
| C. |
| D. |
If both parents are carriers, the chance that a child would be affected is 1/4.
You should use the addition rule to determine the chance that both parents are carriers AND the chance that the child is affected.

A man's paternal grandfather had galactosemia. This is a rare disease caused by the inability to process galactose, leading to muscle, nerve, and kidney malfunction. The man married a woman whose sister had galactosemia but whose parents did not. The woman is now pregnant with their first child.
Unpack the Problem: Break this problem into several parts and arrive at a solution using this guided, step-by-step approach.
- Part A (step 1): Draw the pedigree as described.
- Part B (steps 2-9): Decide what the probability is that this child will have galactosemia.
- Part C (step 10): Resolve what the probability is that a second child will have galactosemia if the first child does, in fact, have it.
If the first child does have galactosemia, what is the probability a second child will have it?
| A. |
| B. |
| C. |
| D. |
When calculating the answer to step 9, you didn’t know whether the parents had the recessive allele for galactosemia; instead, you calculated the probabilities that they did. Does the information that the first child has galactosemia tell you if both parents have the allele?
What does the fact that the first child has galactosemia tell you about the genotypes of the parents?
What is the probability of each parent being a heterozygote? (These probabilities are to be inserted into your calculation 1/4 x ? x ? = probability of next child having galactosemia.)

General Hints
When analyzing a pedigree, there are a few rules of thumb:
- If two affected parents have an unaffected kid, it is NOT recessive.
- If unaffected parents have an affected kid, it is NOT dominant.
- If unaffected parents have an affected daughter, it is NOT dominant or x-linked recessive.
- If an unaffected woman has an affected son, it is NOT x-linked dominant.
- If an affected man has an unaffected daughter, it is NOT x-linked dominant.
- If an affected woman has an unaffected son, it is NOT x-linked recessive.
- If an unaffected man has an affected daughter, it is NOT x-linked recessive.
When calculating probabilities, two rules are useful for predicting the ratios of offspring produced in genetic crosses:
- Multiplication Rule: the probability of two or more independent events occurring together is calculated by multiplying their independent probabilities. e.g., the probability of rolling a die twice and obtaining two threes.
- Addition Rule: the probability of any one of two or more mutually exclusive events is calculated by adding the probabilities of these events. e.g., the probability of rolling either a two or a three.
Punnett squares are also useful tools for determining probability. If you see a certain ratio of affected to unaffected individuals in a generation, it may be helpful to draw the Punnett square to determine the genotype of the parent. For instance, if both the parents are carriers of a recessive trait, you would expect to see a 3:1 ratio, whereas if only one parent is a carrier, you would not have any affected offspring. If an heterozygote is crossed to a homozygous individual (a testcross), you would expect a 1:1 ratio in the progeny. Similarly, a cross between two heterozygotes would yield a 3:1 ratio if it is an example of dominance, or a 1:2:1 ratio if it is "incomplete dominance." This can be easily visualized by drawing Punnett squares with each of the possible genotypes represented.
To Summarize
So, there are a couple of rules to remember when analyzing a pedigree and calculating probability.
In general, if a trait is expressed in every generation, it is probably dominant. If it skips generations, it is probably recessive. Finally, if it seems to affect males more often than females, it is likely to be x-linked.
The probability of having a particular genotype can be calculated using either the product or addition rules. If you want to examine the probability of two children inheriting a particular trait, you would use the multiplication rule. The probabilities are multiplied together to determine the probability of two or more independent events occurring together. If you want to examine the probability of at least one of the two children inheriting a particular trait, you would use the addition rule. The probability of any one of two or more mutually exclusive events is calculated by adding the probabilities of these events.