Chapter 14. Online Dating: Everything up to Factorial ANOVA (two-way between-groups ANOVA)

Introduction

Which Test Is Best?
true
true
You must read each slide, and complete any questions on the slide, in sequence.

Online Dating: Everything up to Factorial ANOVA (two-way between-groups ANOVA)

By: Marsha J. McCartney, University of Kansas, Warren Fass, University of Pittsburgh Bradford, and Susan A. Nolan, Seton Hall University

A woman’s advantage. (2016). The deep end by OkCupid. Retrieved February 5, 2017, from https://www.okcupid.com/deep-end/a-womans-advantage

Introduction

Everything up to Factorial ANOVA (two-way between-groups ANOVA)

appy afro american couple flirting in shopping mall
michaeljung/Shutterstock

Lots of people find dates online. There are plenty of articles about how best to meet someone in the online dating world, and it seems that everyone has an opinion. Can the data collected by these sites shed light on what leads to a successful relationship? That is actually a pretty complex question, statistically speaking, so let’s look at a few different ways that one online dating site, OkCupid, uses data to understand successful online dating.

Guidelines for choosing the appropriate hypothesis test

Choosing the Appropriate Hypothesis Test, Image Long Description

By asking the right questions about our variables and research design, we can choose the appropriate hypothesis test for our research.

Four Categories of Hypothesis Tests (IV = Independent variable; DV = dependent variable)

  • 1. Only scale variables
  • 1.1. Question about association
  • 1.1.1. Pearson correlation coefficient
  • 1.2. Question about prediction
  • 1.2.1. Regression
  • 2. Nominal IV; Scale DV
  • 2.1. One IV
  • 2.1.1. Two groups (levels)
  • 2.1.1.1. One represented by a sample, one by the population
  • 2.1.1.1.1. Mu and sigma known
  • 2.1.1.1.1.1. z test
  • 2.1.1.1.2. Only mu known
  • 2.1.1.1.2.1. Single-sample t-test
  • 2.1.1.2. Two samples
  • 2.1.1.2.1. Within-groups design
  • 2.1.1.2.1.1. Paired-samples t test
  • 2.1.1.2.2. Between-groups design
  • 2.1.1.2.2.1. Independent-samples t test
  • 2.1.2. Three or more groups (levels)
  • 2.1.2.1. Within-groups design
  • 2.1.2.1.1. One-way within-groups ANOVA
  • 2.1.2.2. Between-groups design
  • 2.1.2.2.1. One-way between groups ANOVA
  • 2.2. One-way between groups ANOVA
  • 2.2.1. Factorial ANOVA (e.g., two-way between-groups ANOVA)
  • 3. Only nominal variables
  • 3.1. One nominal variable
  • 3.1.1. Chi-square test for goodness of fit
  • 3.2. Two nominal variables
  • 3.2.1. Chi-square test for independence
  • 4. Any ordinal variables
  • 4.1. Two ordinal variables; question about association
  • 4.1.1. Spearman rank-order correlation coefficient
  • 4.2. Nominal IV and ordinal DV
  • 4.2.1. Within-groups design; two groups
  • 4.2.1.1. Wilcoxon signed-rank test
  • 4.2.2. Between-groups design
  • 4.2.2.1. Two groups
  • 4.2.2.1.1. Mann-Whitney U test
  • 4.2.2.2. Three or more groups
  • 4.2.2.2.1. Kruskal-Wallis H test

    • Example 1 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    One of the surprising findings presented in the OkCupid article, “A women’s advantage,” was that women prefer to split the bill on a first date more than men. Imagine that we recruited 20 male and 20 female undergraduates. We ask the participants to rate the likelihood, on a 5-point rating scale (1 = never, 5 = always), that they would want to split the bill on a first date.

    Which statistical test could be used to determine if there was a significant difference in preference ratings between the two groups?

    Question

    La87Q+SOXoXwjGGneRTBfwcJgrnguyxqmcWUSz4HjQXQ1mF6032cwhkfXIIo7Ebwmdk3z3BE+b5AOK0eNtE65SjI88EySHYscGCtxYICbBmF5KIDMKRVKCd+S9Fq6opQNzlcZnuX0bXH62MvdvDR0eoEJ+2/+T/vaA2B1NsNxDj8VOgY9b1jBi/aKKMp8JlhsW0Jel05kLpeHIsNgBeFNTtyKUC9lFlIBpaA48n7krQECzpo9uGZ5gODcqNORS8iPNy+i6Wp7XCsSREopLLpyuohZ4YPZ9+VWm/tiX0j7I254KcOQMKenL5hgvNooBmRMyM0/Ru9waexuz5slWjkvof0eX941oICLmkLCgePPFb+lMNIeNZvzcqda9gCLNWki85WH/+aTRCYNwUR2QLbbenV+NcJ6ZqovTcgRbdVxYcX7cwnjH3GXACBVv3uXd2f7lzsqpb/qxQUiQEyDtI2JJdmXWTzfQeT6MOi6I2FFiEL3Ab5o/iCjA==
    Correct! The researchers could have used an independent-samples t test, because there is one nominal independent variable, gender, with two levels or groups: male and female undergraduates. There is a scale dependent variable, likelihood ratings. And participants are only in one of the two groups, so it is a between-groups design.
     
    Now skip ahead to the next example by clicking here. Or, for more practice walking through the flowchart questions, simply click the Next button in the bottom right corner of the screen.
    Actually, that’s not the correct statistical analysis. Let’s walk through the questions on the flowchart in Appendix E to determine what analysis could be used in this case.

    Example 1 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    In which of the following four categories does this situation fall? Click to see the data again. And click on the flowchart button to see the overview for choosing the best test.

    One of the surprising findings presented in the OkCupid article, “A women’s advantage,” was that women prefer to split the bill on a first date more than men. Imagine that we recruited 20 male and 20 female undergraduates. We ask the participants to rate the likelihood, on a 5-point rating scale (1 = never, 5 = always), that they would want to split the bill on a first date.

    Question

    gkkMMcIDU6Sk/hqnYAvNuff6SNWH2Dc5b71a0WNQELw0PH+TwojgZgd0kWEqTvT4N/MmPw2F15iVOQ3TWaLD2k7fiYMzcaMAl8b6viJm/D1bJkqmzgCUUa3kcAM71AMB7YyBGibig5iG9Dwnkjrwgm10hilXUgSW/P1TczdIQ+oa9g0jQLRbU/LvzurchXfzyOKBYNRBR9uS/M/8yAVLajhhAGVf1KBBqGkkfdRcKemmgY+5/DdP7tCmwlfaCWOBKYjegYsXFdlinUCp0gYjaGurZ2nTYXxn5KiLNwJAIECjYBsr0PdZ0wjfsgCaekh0KZr1jb7cWhnqdYhdMxNfQxjeborjzQRwVJc0Joyx50YZEaUYneA3QA==
    Correct! There is at least one nominal independent variable and a scale dependent variable.
    Actually, there is at least one nominal independent variable and a scale dependent variable.

    Example 1 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many nominal independent variables are there?

    Question

    NmfX3PywsY556Fm5UMZd1mXX2ROSfZoNHvuq8AQgX+LYbcgFd3WxiSxQpLOTRo3k9SDEwIqsg2+gF+Mox5rt6s2cg9o3fLeWIblXCkWkaK9HL1iDpDYXTfLXw0CjifvaWWKCtJ6RBAIeWPARzIj5MIko7MSgLuvfT8eIwQ==
    Correct! There is one nominal independent variable, gender. (The dependent variable, likelihood ratings, is scale.)
    Actually, there is one nominal independent variable, gender. (The dependent variable, likelihood ratings, is scale.)

    Example 1 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many levels does the independent variable have?

    Question

    t1VpaahHGKTRHTD24jDcDmAj4sSmScIg2naP5NWhinvNZ+M0uD8BhoDJgb/6b/rXyyuAUpMaL3aKOZw55EL42Ye5vUZBhY/HTXP3V4wv1IjdNbvCOEFXdPXvtVc2EO0yPByDvc/x8usJdgBXKkSJ5w==
    Correct! There are two levels or groups.
    Actually, there are two levels or groups.

    Example 1 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many samples are there?

    Question

    2NV+iWDFlmeer3owksM55Ju2+NBNvaJeU8edg5blK9+EvJQ2gh4RfGCG4fyn78Y7j4HjQeyA1Vl12vesx6nY4RFgMSNCoNancYeN2W5TQ0yvXVEgBznuSUsqSasFIm1yXIdG+aeliQ8b88EMd6gSMbPy1ixtYEMDMMLMIzHU7dJlXQ3SADsCmkS693Pzq3E+VY2SsNrnA9FVamwL1gWbAJ8l3BxOFnqXo8ofzI9JKmE=
    Correct! There are two samples, one consisting of male undergraduates and one consisting of female undergraduates.
    Actually, there are two samples, one consisting of male undergraduates and one consisting of female undergraduates.

    Example 1 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    What type of design is this?

    Question

    CDx0RccBOaHuUkd1VF2jWDCFeUEqYoktqTWym2P35XhvtK7I8YUzIJQzav085gEKZoJSthZ/RMr9IlBHXpBUMs0A5/W/2Arvr2kRAm6kfL04hNpAjsRReOHsZW8XPyBLasDd6F+u1FYn+G+lSBlZJg==
    Correct! This is a between-groups design. Each participant appears in only one of the two groups.
    Actually, this is a between-groups design. Each participant appears in only one of the two groups.

    Example 1 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    Based on the answers to these questions, what statistical analysis could be used to determine if there was a significant difference in preference ratings between the two groups?

    Question

    La87Q+SOXoXwjGGneRTBfwcJgrnguyxqmcWUSz4HjQXQ1mF6032cwhkfXIIo7Ebwmdk3z3BE+b5AOK0eNtE65SjI88EySHYscGCtxYICbBmF5KIDMKRVKCd+S9Fq6opQNzlcZnuX0bXH62MvdvDR0eoEJ+2/+T/vaA2B1NsNxDj8VOgY9b1jBi/aKKMp8JlhsW0Jel05kLpeHIsNgBeFNTtyKUC9lFlIBpaA48n7krQECzpo9uGZ5gODcqNORS8iPNy+i6Wp7XCsSREopLLpyuohZ4YPZ9+VWm/tiX0j7I254KcOQMKenL5hgvNooBmRMyM0/Ru9waexuz5slWjkvof0eX941oICLmkLCgePPFb+lMNIeNZvzcqda9gCLNWki85WH/+aTRCYNwUR2QLbbenV+NcJ6ZqovTcgRbdVxYcX7cwnjH3GXACBVv3uXd2f7lzsqpb/qxQUiQEyDtI2JJdmXWTzfQeT6MOi6I2FFiEL3Ab5o/iCjA==
    Correct! TThe researchers could have used an independent-samples t test, because there is one nominal independent variable, gender, with two levels or groups: male and female undergraduates. There is a scale dependent variable, likelihood ratings. And participants are only in one of the two groups, so it is a between-groups design.
    Actually, that’s not the correct statistical analysis. The researchers could have used an independent-samples t test, because there is one nominal independent variable, gender, with two levels or groups: male and female undergraduates. There is a scale dependent variable, likelihood ratings. And participants are only in one of the two groups, so it is a between-groups design.

    Example 2 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    OkCupid also provided information about the numbers of messages sent by men and women in relation to their ages. OkCupid looked at different age ranges (e.g., 21-30-years-old, 31-40-years-old) and counted the number of messages sent by men and women from each age range. Imagine that OkCupid provided us with the following data from one month: The total number of messages sent for 50 men and 50 women from both of the following age groups, between 21-30-years-old and between 31-40-years old. We would then have data from 200 users of OkCupid.

    Which statistical test could be used to determine if there were significant differences in the number of messages sent among the four groups?

    Question

    hrV4ticNKcBDcUrtUu62Q8hqhJ3ChNZd9ED/ub/Logn6Si3pQrfxyqML2O92uIzmJd8y8NPoqiMButqIekWdumvdxXagZg0G0vY7sAe4SpK3V5ioO9xGcHclSGCI559yE8WCufYNvjxTCYfG0CYSJjkSS0YE+/Pl9I6W8yk6nh4P2HArlFjWmnHdHhHa4TeUZRk3xYEVC/UWAbK2tLS2Ojkmh8cpZO+soVE491S3HCmKMn52+z2knfyaNHE3FVWQjYKY03p7ISL5KoDPi0WUe9mSZQYutDivGOF1svlLEP9dJx7fsCuMI4xKEB9o128jyKUrTzyEps9wJbvmmfmXfuRO/0cuaxW06xWPxvq/LD+WY5Ht785opsE1DDegqjlRJteCmKBYmPBAZ1aETrWIaHYH7XZJUCritU2sjWo0BR4Jbll7WiFckmQ7Q8QAfQtG984wxKBJOH0aEHSy/n7KPAd23ktWe2U+oKTbiLq9+HhN4iOfKGENNg==
    Correct! The researchers could have used a two-way between-groups ANOVA, because there are two nominal independent variables, gender and age range. Gender has two levels or groups, men and women, and age range has two levels or groups, 21-30 and 31-40. There is a scale dependent variable, number of messages. And participants are only in one of the four groups, so it is a between-groups design.
     
    Now skip ahead to the next example by clicking here. Or, for more practice walking through the flowchart questions, simply click the Next button in the bottom right corner of the screen.
    Actually, that’s not the correct statistical analysis. Let’s walk through the questions on the flowchart in Appendix E to determine what analysis could be used in this case.

    Example 2 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    In which of the following four categories does this situation fall? Click to see the data again. And click on the flowchart button to see the overview for choosing the best test.

    OkCupid also provided information about the number of messages sent by men and women in relation to their ages. OkCupid looked at different age ranges (e.g., 21-30-yrs-old, 31-40-yrs-old) and counted the number of messages sent by men and women from each age range.. Imagine that OkCupid provided us with the following data from one month (e.g., May 2016): The total number of messages sent for 50 men and 50 women from both of the following age groups; between 21-30-yrs-old and between 31-40-yrs old. We would then have data from 200 users of OkCupid.

    Question

    gkkMMcIDU6Sk/hqnYAvNuff6SNWH2Dc5b71a0WNQELw0PH+TwojgZgd0kWEqTvT4N/MmPw2F15iVOQ3TWaLD2k7fiYMzcaMAl8b6viJm/D1bJkqmzgCUUa3kcAM71AMB7YyBGibig5iG9Dwnkjrwgm10hilXUgSW/P1TczdIQ+oa9g0jQLRbU/LvzurchXfzyOKBYNRBR9uS/M/8yAVLajhhAGVf1KBBqGkkfdRcKemmgY+5/DdP7tCmwlfaCWOBKYjegYsXFdlinUCp0gYjaGurZ2nTYXxn5KiLNwJAIECjYBsr0PdZ0wjfsgCaekh0KZr1jb7cWhnqdYhdMxNfQxjeborjzQRwVJc0Joyx50YZEaUYneA3QA==
    Correct! There is at least one nominal independent variable and a scale dependent variable.
    Actually, there is at least one nominal independent variable and a scale dependent variable.

    Example 2 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many nominal independent variables are there?

    Question

    Bm/jboLroAzpfYuUyC5pxuhLgxJA3JV6PbV6tq57xOwfvobDJt1LhFAe48miCjpmwMGA6JuKpuPNBFVzOp+kGNi+nywSakMKjjlY+TFk9xahy8KQdl/IGuI40HoGabOn03sId0DN2j7HHiUtHDhO42zF4v4utQ3NFSIIFP1Rcjf/MzN3
    Correct! There are two nominal independent variables, gender and age range. (The dependent variable, number of messages sent, is scale.) At this point, the flowchart tells us that we should use some kind of a factorial ANOVA. Appendix E directs us to the first table in the chapter on two-way between-groups ANOVA for further instructions. In the first column, it tells us that this is a two-way ANOVA because there are two nominal independent variables.
    Actually, there are two nominal independent variables, gender and age range. (The dependent variable, number of messages sent, is scale.) At this point, the flowchart tells us that we should use some kind of a factorial ANOVA. Appendix E directs us to the first table in the chapter on two-way between-groups ANOVA for further instructions. In the first column, it tells us that this is a two-way ANOVA because there are two nominal independent variables.

    Example 2 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    The then tells us to decide: What type of design is this?

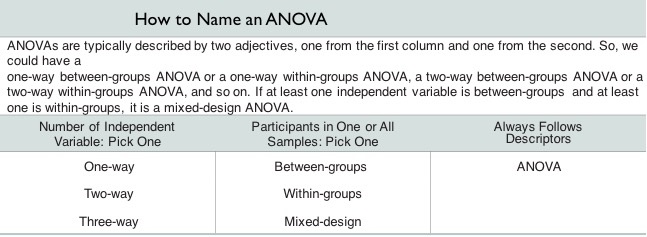
    ANOVAs are typically described by two adjectives, one from the first column and one from the second. So,we could have a one-way between-groups ANOWA or a one-way within-groups ANOVA, a two-way between-groups ANOVA or a two-way within-groups ANOVA, and so on. If at least one independent varibale is between-groups and at least one is within-groups

    Question

    CDx0RccBOaHuUkd1VF2jWDCFeUEqYoktqTWym2P35XhvtK7I8YUzIJQzav085gEKZoJSthZ/RMr9IlBHXpBUMs0A5/W/2Arvr2kRAm6kfL04hNpAjsRReOHsZW8XPyBLasDd6F+u1FYn+G+lSBlZJg==
    Correct! Each participant appears in only one of the four groups, so it is a between-groups design.
    Actually, each participant appears in only one of the four groups, so it is a between-groups design.

    Example 2 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    Based on the answers to these questions, what statistical analysis could be used to determine if there were significant differences in the number of messages sent among the four groups?

    Question

    hrV4ticNKcBDcUrtUu62Q8hqhJ3ChNZd9ED/ub/Logn6Si3pQrfxyqML2O92uIzmJd8y8NPoqiMButqIekWdumvdxXagZg0G0vY7sAe4SpK3V5ioO9xGcHclSGCI559yE8WCufYNvjxTCYfG0CYSJjkSS0YE+/Pl9I6W8yk6nh4P2HArlFjWmnHdHhHa4TeUZRk3xYEVC/UWAbK2tLS2Ojkmh8cpZO+soVE491S3HCmKMn52+z2knfyaNHE3FVWQjYKY03p7ISL5KoDPi0WUe9mSZQYutDivGOF1svlLEP9dJx7fsCuMI4xKEB9o128jyKUrTzyEps9wJbvmmfmXfuRO/0cuaxW06xWPxvq/LD+WY5Ht785opsE1DDegqjlRJteCmKBYmPBAZ1aETrWIaHYH7XZJUCritU2sjWo0BR4Jbll7WiFckmQ7Q8QAfQtG984wxKBJOH0aEHSy/n7KPAd23ktWe2U+oKTbiLq9+HhN4iOfKGENNg==
    Correct! The researchers could have used a two-way between-groups ANOVA, because there are two nominal independent variables, gender and age range. Gender has two levels or groups, men and women, and age range has two levels or groups, 21-30 and 31-40. There is a scale dependent variable, number of messages. And participants are only in one of the four groups, so it is a between-groups design.
    Actually, that’s not the correct statistical analysis. The researchers could have used a two-way between-groups ANOVA, because there are two nominal independent variables, gender and age range. Gender has two levels or groups, men and women, and age range has two levels or groups, 21-30 and 31-40. There is a scale dependent variable, number of messages. And participants are only in one of the four groups, so it is a between-groups design.

    Example 3 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    Another interesting OkCupid finding concerned who was more likely to send a first message to another OkCupid member. OkCupid reported that the sender’s gender and sexual orientation had an impact on the likelihood of sending a first message, but only for male senders. That is, heterosexual men were more likely than gay men and bisexual men to send a first message to another member of OkCupid. However, that difference was not found among heterosexual women, lesbians, and bisexual women.
    For this example, imagine that we recruited 30 heterosexual men, 30 gay men, and 30 bisexual men. We ask the men to rate, on a 7-point scale, the likelihood (1 = not very, 7 = very) that they would send the first message to another member from OkCupid.

    Which statistical test could be used to determine if there was a significant difference in likelihood ratings among the three groups?

    Question

    PRKx+pz2l50ki/1XftKBobb6xNgJDYNAqKe2G/D2em0FQiToOvnem3So/Mopmzsxd2GtSpwKkkpdNIAp8lNkVb6bSIqo8VUpiBOoejw6ZAYmCTpZ2v+0L9kbNqF+pe0LoYMYF4+29/6OWFjoEz6Zn5WvMnKD3X1ONneBp40YH8KfOJvNE5tBobmqypwmtblvWcMZUmmFmdLZeMfuD2dokgbw+LPEUfFL8S0olDlFw+bt9YVXcDL0hwa9QGqArkHuUG65M95dX7rZNR7Yi/Ehmh30WfZAohD8SK9v35Y7egx4kV0cdhsNvvwQ+RxPWGrVzhHanZh3I/4Sq75ZcKTOtJjE4r34Lel7f0b7m27bVbX2l1T7+KHaD8nEvYL53ry+nf2zwPaUs+u4lVQiY0O/15qQzerzLJDAKXTV4FbnpEbMSGIPSabwoP1J0dYXyXCmoIVc9tiIC0S7yM4HIsfkmj6C/5wHU8FDtIAQ/GsCjTrlXgZruW5tGA==
    Correct! The researchers could have used a one-way between-groups ANOVA, because there is one nominal independent variable, sexual orientation, with three levels or groups: heterosexual men, gay men, and bisexual men. There is a scale dependent variable, likelihood rating. And participants are only in one of the three groups, so it is a between-groups design.
     
    Now skip ahead to the next example by clicking here. Or, for more practice walking through the flowchart questions, simply click the Next button in the bottom right corner of the screen.
    Actually, that’s not the correct statistical analysis. Let’s walk through the questions on the flowchart in Appendix E to determine what analysis could be used in this case.

    Example 3 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    In which of the following four categories does this situation fall? Click to see the data again. And click on the flowchart button to see the overview for choosing the best test.

    Another interesting OkCupid finding concerned who was more likely to send a first message to another OkCupid member. OkCupid reported that the sender’s gender and sexual orientation had an impact on the likelihood of sending a first message, but for only male senders. That is, heterosexual men were more likely than gay men and bisexual men to send a first message to another member of OkCupid. However, that difference was not found among heterosexual women, lesbians, and bisexual women. For this example, imagine that we recruited 30 heterosexual men, 30 gay men, and 30 bisexual men. We ask the men to rate, on a 7-point scale, the likelihood (1 = not very, 7 = very) that they would send the first message to another member from OkCupid.

    Question

    gkkMMcIDU6Sk/hqnYAvNuff6SNWH2Dc5b71a0WNQELw0PH+TwojgZgd0kWEqTvT4N/MmPw2F15iVOQ3TWaLD2k7fiYMzcaMAl8b6viJm/D1bJkqmzgCUUa3kcAM71AMB7YyBGibig5iG9Dwnkjrwgm10hilXUgSW/P1TczdIQ+oa9g0jQLRbU/LvzurchXfzyOKBYNRBR9uS/M/8yAVLajhhAGVf1KBBqGkkfdRcKemmgY+5/DdP7tCmwlfaCWOBKYjegYsXFdlinUCp0gYjaGurZ2nTYXxn5KiLNwJAIECjYBsr0PdZ0wjfsgCaekh0KZr1jb7cWhnqdYhdMxNfQxjeborjzQRwVJc0Joyx50YZEaUYneA3QA==
    Correct! There is at least one nominal independent variable and a scale dependent variable.
    Actually, there is at least one nominal independent variable and a scale dependent variable.

    Example 3 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many nominal independent variables are there?

    Question

    NmfX3PywsY556Fm5UMZd1mXX2ROSfZoNHvuq8AQgX+LYbcgFd3WxiSxQpLOTRo3k9SDEwIqsg2+gF+Mox5rt6s2cg9o3fLeWIblXCkWkaK9HL1iDpDYXTfLXw0CjifvaWWKCtJ6RBAIeWPARzIj5MIko7MSgLuvfT8eIwQ==
    Correct! There is one nominal independent variable, sexual orientation. (The dependent variable, likelihood rating, is scale.)
    Actually, there is one nominal independent variable, sexual orientation. (The dependent variable, likelihood rating, is scale.)

    Example 3 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many levels does the independent variable have?

    Question

    yTJhBUq5mbELo7JTE+uIqQee6TRdauOLAdy5Hw7Lg9P15o+FGyRzfuEbmfCENBA5unVpyh7htT/hWDXRrhuQIWxZvQjr8TVJ5WYTOdGBzWK/zcXYULq6GuzRg1UHqPcYQc5CGG8uqgtBb9r7wXrvl5JQYWnFmWRvhwuvwFZlUDKBfYcv
    Correct! There are three levels or groups: heterosexual men, gay men, and bisexual men.
    Actually, there are there are three levels or groups: heterosexual men, gay men, and bisexual men.

    Example 3 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    What type of design is this?

    Question

    CDx0RccBOaHuUkd1VF2jWDCFeUEqYoktqTWym2P35XhvtK7I8YUzIJQzav085gEKZoJSthZ/RMr9IlBHXpBUMs0A5/W/2Arvr2kRAm6kfL04hNpAjsRReOHsZW8XPyBLasDd6F+u1FYn+G+lSBlZJg==
    Correct! This is a between-groups design. Each participant appears in only one of the three groups.
    Actually, this is a between-groups design. Each participant appears in only one of the three groups.

    Example 3 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    Based on the answers to these questions, what statistical analysis could be used to determine if there was a significant difference in likelihood ratings among the three groups?

    Question

    PRKx+pz2l50ki/1XftKBobb6xNgJDYNAqKe2G/D2em0FQiToOvnem3So/Mopmzsxd2GtSpwKkkpdNIAp8lNkVb6bSIqo8VUpiBOoejw6ZAYmCTpZ2v+0L9kbNqF+pe0LoYMYF4+29/6OWFjoEz6Zn5WvMnKD3X1ONneBp40YH8KfOJvNE5tBobmqypwmtblvWcMZUmmFmdLZeMfuD2dokgbw+LPEUfFL8S0olDlFw+bt9YVXcDL0hwa9QGqArkHuUG65M95dX7rZNR7Yi/Ehmh30WfZAohD8SK9v35Y7egx4kV0cdhsNvvwQ+RxPWGrVzhHanZh3I/4Sq75ZcKTOtJjE4r34Lel7f0b7m27bVbX2l1T7+KHaD8nEvYL53ry+nf2zwPaUs+u4lVQiY0O/15qQzerzLJDAKXTV4FbnpEbMSGIPSabwoP1J0dYXyXCmoIVc9tiIC0S7yM4HIsfkmj6C/5wHU8FDtIAQ/GsCjTrlXgZruW5tGA==
    Correct! The researchers could have used a one-way between-groups ANOVA, because there is one nominal independent variable, sexual orientation, with three levels or groups: heterosexual men, gay men, and bisexual men. There is a scale dependent variable, likelihood rating. And participants are only in one of the three groups, so it is a between-groups design.
    Actually, that’s not the correct statistical analysis. The researchers could have used a one-way between-groups ANOVA, because there is one nominal independent variable, sexual orientation, with three levels or groups: heterosexual men, gay men, and bisexual men. There is a scale dependent variable, likelihood rating. And participants are only in one of the three groups, so it is a between-groups design.

    Example 4 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    OkCupid also provided data indicating that if heterosexual women were interested in sending the first message to heterosexual men, the heterosexual women would perceive the heterosexual men’s attractiveness to be greater than their own attractiveness. That is, the heterosexual woman would be more likely to send the first message if she perceived the heterosexual man’s attractiveness to be greater than her attractiveness. Imagine that we recruited 120 heterosexual women and asked each to view two pictures of heterosexual men. The pictures were previously sorted for perceived attractiveness by each woman, which resulted in identifying two different pictures. One picture would be of a man perceived to be more attractive than the woman, and one picture would be of a man perceived to be less attractive than the woman. We then ask the woman to rate both pictures for the likelihood (1 = not very, 10 = very) she would send the first message to the man depicted in each picture.

    Which statistical test could be used to determine if there was a significant difference in the likelihood ratings between the two groups?

    Question

    8xikYm+8CsGPgjRIkH8SeMxFL5c43uhvSjiAgSx6lU8n5ISjPI3+SEL4O98DLa33KLECYJH4z8hNC3iPqoxh0U8IMk2T6nvuvzUFQCWqRvdni6Iy67qaj0wgIXk/hVgeMeYIIR4V9u4fqMbkYIcr2ilAicizpXysJ3n2H+6McgMZh8Uzaf5w7hPqxWROoh4kDKBvoqdw7FUgKFM/+rvbTLSIVbEmIvmvSErnv+nvx71SvxLY5jugd6SPzEf12wNp1prA2/eLltcoxjUnaSu3qt9CwYEDibjfU+7XzhF3MXDGIiYR+S+olV6uL/hnFjQKYLb2YT4buCJqDlZ1Juhdw8t6nz7BrI4tm2g10don4SNp1oBzCVn5s6oT3ihzQZ20GCXOUEuplXXskT6+9HkxZpb67yeZ0SM0lMSkGCL21TAAFRCvbx3umEqQhHL24lj4QzxjI1l5nWIOwWs1PaLa8Q+vxAuW4Z7InbE2dM7u33zxVw941XOJeA==
    Correct! The researchers could have used a paired-samples t test because there is one nominal independent variable, attractiveness of picture, with two levels or groups: more attractive and less attractive. There is a scale dependent variable, likelihood rating. And participants are in both of the two groups, so it is a within-groups design.
     
    Now skip ahead to the next example by clicking here. Or, for more practice walking through the flowchart questions, simply click the Next button in the bottom right corner of the screen.
    Actually, that’s not the correct statistical analysis. Let’s walk through the questions on the flowchart in Appendix E to determine what analysis could be used in this case.

    Example 4 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    In which of the following four categories does this situation fall? Click to see the data again. And click on the flowchart button to see the overview for choosing the best test.

    OkCupid also provided data indicating that if heterosexual women were interested in sending the first message to heterosexual men, the heterosexual women would perceive the heterosexual men’s attractiveness to be greater than their own attractiveness. That is, the heterosexual woman would be more likely to send the first message if she perceived the heterosexual man’s attractiveness to be greater than her attractiveness. Imagine that we recruited 120 heterosexual women and asked each to view two pictures of heterosexual men. The pictures were previously sorted for perceived attractiveness by each woman, which resulted in identifying two different pictures. One picture would be of a man perceived to be more attractive than the women, and one picture would be of a man perceived to be less attractive than the women. We then ask the women to rate both pictures for the likelihood (1 = not very, 10 = very) they would send the first message to the man depicted in each picture.

    Question

    gkkMMcIDU6Sk/hqnYAvNuff6SNWH2Dc5b71a0WNQELw0PH+TwojgZgd0kWEqTvT4N/MmPw2F15iVOQ3TWaLD2k7fiYMzcaMAl8b6viJm/D1bJkqmzgCUUa3kcAM71AMB7YyBGibig5iG9Dwnkjrwgm10hilXUgSW/P1TczdIQ+oa9g0jQLRbU/LvzurchXfzyOKBYNRBR9uS/M/8yAVLajhhAGVf1KBBqGkkfdRcKemmgY+5/DdP7tCmwlfaCWOBKYjegYsXFdlinUCp0gYjaGurZ2nTYXxn5KiLNwJAIECjYBsr0PdZ0wjfsgCaekh0KZr1jb7cWhnqdYhdMxNfQxjeborjzQRwVJc0Joyx50YZEaUYneA3QA==
    Correct! There is at least one nominal independent variable and a scale dependent variable.
    Actually, there is at least one nominal independent variable and a scale dependent variable.

    Example 4 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many nominal independent variables are there?

    Question

    NmfX3PywsY556Fm5UMZd1mXX2ROSfZoNHvuq8AQgX+LYbcgFd3WxiSxQpLOTRo3k9SDEwIqsg2+gF+Mox5rt6s2cg9o3fLeWIblXCkWkaK9HL1iDpDYXTfLXw0CjifvaWWKCtJ6RBAIeWPARzIj5MIko7MSgLuvfT8eIwQ==
    Correct! There is one nominal independent variable, attractiveness. (The dependent variable, likelihood rating, is scale.)
    Actually, there is one nominal independent variable, attractiveness. (The dependent variable, likelihood rating, is scale.)

    Example 4 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many levels does the independent variable have?

    Question

    t1VpaahHGKTRHTD24jDcDmAj4sSmScIg2naP5NWhinvNZ+M0uD8BhoDJgb/6b/rXyyuAUpMaL3aKOZw55EL42Ye5vUZBhY/HTXP3V4wv1IjdNbvCOEFXdPXvtVc2EO0yPByDvc/x8usJdgBXKkSJ5w==
    Correct! There are two levels or groups.
    Actually, there are two levels or groups.

    Example 4 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many samples are there?

    Question

    2NV+iWDFlmeer3owksM55Ju2+NBNvaJeU8edg5blK9+EvJQ2gh4RfGCG4fyn78Y7j4HjQeyA1Vl12vesx6nY4RFgMSNCoNancYeN2W5TQ0yvXVEgBznuSUsqSasFIm1yXIdG+aeliQ8b88EMd6gSMbPy1ixtYEMDMMLMIzHU7dJlXQ3SADsCmkS693Pzq3E+VY2SsNrnA9FVamwL1gWbAJ8l3BxOFnqXo8ofzI9JKmE=
    Correct! There are two samples, one consisting of more attractive pictures and one consisting of less attractive pictures.
    Actually, there are two samples, one consisting of more attractive pictures and one consisting of less attractive pictures.

    Example 4 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    What type of design is this?

    Question

    6FNIgWDYUsgGpUPNrs7Hs99wloy08LoQ7oJhDxxI+28BvIIePz0SlA1F5fbzTNHrRhyaalWVnCXh6yXVbLqDdM/iwSNfyY+bd86uMeLNvIUURUySd3H1XAmRSJmK91wMjAuFrMJlQweX8J+wGOW+0w==
    Correct! This is a within-groups design. Each participant is in both groups.
    Actually, this is a within-groups design. Each participant is in both groups.

    Example 4 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    Based on the answers to these questions, what statistical analysis could be used to determine if there was a significant difference in likelihood ratings between the two groups?

    Question

    8xikYm+8CsGPgjRIkH8SeMxFL5c43uhvSjiAgSx6lU8n5ISjPI3+SEL4O98DLa33KLECYJH4z8hNC3iPqoxh0U8IMk2T6nvuvzUFQCWqRvdni6Iy67qaj0wgIXk/hVgeMeYIIR4V9u4fqMbkYIcr2ilAicizpXysJ3n2H+6McgMZh8Uzaf5w7hPqxWROoh4kDKBvoqdw7FUgKFM/+rvbTLSIVbEmIvmvSErnv+nvx71SvxLY5jugd6SPzEf12wNp1prA2/eLltcoxjUnaSu3qt9CwYEDibjfU+7XzhF3MXDGIiYR+S+olV6uL/hnFjQKYLb2YT4buCJqDlZ1Juhdw8t6nz7BrI4tm2g10don4SNp1oBzCVn5s6oT3ihzQZ20GCXOUEuplXXskT6+9HkxZpb67yeZ0SM0lMSkGCL21TAAFRCvbx3umEqQhHL24lj4QzxjI1l5nWIOwWs1PaLa8Q+vxAuW4Z7InbE2dM7u33zxVw941XOJeA==
    Correct! The researchers could have used a paired-samples t test because there is one nominal independent variable, attractiveness of picture, with two levels or groups, more attractive and less attractive. There is a scale dependent variable, likelihood rating. And participants are in both of the two groups, so it is a within-groups design.
    Actually, that’s not the correct statistical analysis. The researchers could have used a paired-samples t test because there is one nominal independent variable, attractiveness of picture, with two levels or groups, more attractive and less attractive. There is a scale dependent variable, likelihood rating. And participants are in both of the two groups, so it is a within-groups design.

    Example 5 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    Let’s look at one final research finding from OkCupid. We frequently do not send an immediate response to email messages; our email inboxes have an accumulation of messages waiting for our responses. The same is true when using online dating sites. OkCupid found that, for heterosexual men, the number of messages received had an impact on the probability they would respond to all of their messages. That is, the more messages in a person’s inbox without a response, the more likely the person would send a response to all of the messages. Imagine that we recruited 120 heterosexual men. We show each person three message inboxes containing different ranges of messages without a response: 20-39, 40-59, and 60-79. For each message inbox, we ask each man to rate the degree of probability (1 = low probability, 7 = high probability) that they would respond to all the messages within 48 hours.

    Which statistical test could be used to determine if there was a significant difference in probability ratings among the three groups?

    Question

    ApBZxU5cu/XS9eEZysSRFWqt8NH8zu6iPDpFvJlzDzEDKd4GsaV5YnbbaTjr/HYj4eq2/hkm81Y+1cwr8e5nzL2WLE7JL/kgTYg9Kvpka67MYdj4b4D2xCk59I0Gg/5vLJSS/L6AQSHVr9ZBYidY0qMPenNfoMQjUv/8A8Ytov/n8U03CAHDWzIg+dW/r2SdCLN2bgNvNJ2igNk9k7XSNdetnLo1i26pJtmsKe32dJtG3gHree7lighcJ+D+ego48C+aeQTQCHvR4W+9dV7XsqZwdNMtFzMazPA3cGGBm2Nbzh9evGx4+AmC9DLXPJy5Wzcmy0wsBlXPfezmdqTfh6o4kON9oqtjXKLE+z1UwGQHxa2TCqiqGtCmT4KrXXgyPMJ7WBE4jX/Jk7L7BkIB00UTLC5xNSmw9hsXqNCr0Yr+a/dHL3G/zd+Jx9pN2uSzk5Lq6EcPClpjGNR6dOM2t+zpD71T0cSnNFiKxF1F/Qb2yd72qCxmfQ==
    Correct! The researchers could have used a one-way within-groups ANOVA, because there is one nominal independent variable, number of messages, with three levels or groups: 20-39, 40-59, and 60-79. There is a scale dependent variable, probability rating. And participants are in each of the three groups, so it is a within-groups design.
     
    Now skip ahead to the end of the activity by clicking here. Or, for more practice walking through the flowchart questions, simply click the Next button in the bottom right corner of the screen.
    Actually, that’s not the correct statistical analysis. Let’s walk through the questions on the flowchart in Appendix E to determine what analysis could be used in this case.

    Example 5 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    In which of the following four categories does this situation fall? Click to see the data again. And click on the flowchart button to see the overview for choosing the best test.

    Let’s look at one final research finding from OkCupid. We frequently do not send an immediate response to email messages; our email inboxes have an accumulation of messages waiting for our responses. The same is true when using online dating sites. OkCupid found that, for heterosexual men, the number of messages received had an impact on the likelihood they would respond to all of their messages. That is, the more messages in a person’s inbox without a response, the more likely the person would send a response to all of the messages. Imagine that we recruited 120 heterosexual men. We show each person three message inboxes containing different ranges of messages without a response: 20-39, 40-59, and 60-79. For each message inbox, we ask each man to rate the degree of probability (1 = low probability, 7 = high probability) that they would respond to all the messages within 48 hours.

    Question

    gkkMMcIDU6Sk/hqnYAvNuff6SNWH2Dc5b71a0WNQELw0PH+TwojgZgd0kWEqTvT4N/MmPw2F15iVOQ3TWaLD2k7fiYMzcaMAl8b6viJm/D1bJkqmzgCUUa3kcAM71AMB7YyBGibig5iG9Dwnkjrwgm10hilXUgSW/P1TczdIQ+oa9g0jQLRbU/LvzurchXfzyOKBYNRBR9uS/M/8yAVLajhhAGVf1KBBqGkkfdRcKemmgY+5/DdP7tCmwlfaCWOBKYjegYsXFdlinUCp0gYjaGurZ2nTYXxn5KiLNwJAIECjYBsr0PdZ0wjfsgCaekh0KZr1jb7cWhnqdYhdMxNfQxjeborjzQRwVJc0Joyx50YZEaUYneA3QA==
    Correct! There is at least one nominal independent variable and a scale dependent variable.
    Actually, there is at least one nominal independent variable and a scale dependent variable.

    Example 5 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many nominal independent variables are there?

    Question

    NmfX3PywsY556Fm5UMZd1mXX2ROSfZoNHvuq8AQgX+LYbcgFd3WxiSxQpLOTRo3k9SDEwIqsg2+gF+Mox5rt6s2cg9o3fLeWIblXCkWkaK9HL1iDpDYXTfLXw0CjifvaWWKCtJ6RBAIeWPARzIj5MIko7MSgLuvfT8eIwQ==
    Correct! There is one nominal independent variable, number of messages. (The dependent variable, probability rating, is scale.)
    Actually, there is one nominal independent variable, number of messages. (The dependent variable, probability rating, is scale.)

    Example 5 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    How many levels does the independent variable have?

    Question

    skNA66n+M9vPlt+G0bEIzaMgH7DeynOctY853HyPpe9VAyfpezvmzRWISDvepchfMqvtLPAqMexiE8z/L6eMA7xDtFLTZAQ1Wt9wkh7Iceytc7UbDzkCtS+BM/uM1JiAvvW09GFDT/0/OkhnZ5RUAg==
    Correct! There are three levels or groups, 20-39, 40-59, and 60-79.
    Actually, there are there are three levels or groups, 20-39, 40-59, and 60-79.

    Example 5 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    What type of design is this?

    Question

    6FNIgWDYUsgGpUPNrs7Hs99wloy08LoQ7oJhDxxI+28BvIIePz0SlA1F5fbzTNHrRhyaalWVnCXh6yXVbLqDdM/iwSNfyY+bd86uMeLNvIUURUySd3H1XAmRSJmK91wMjAuFrMJlQweX8J+wGOW+0w==
    Correct! This is a within-groups design. Each participant appears in each of the three groups.
    Actually, this is a within-groups design. Each participant appears in each of the three groups.

    Example 5 of 5

    Everything up to Factorial ANOVA (two-way between-groups ANOVA)

    Based on the answers to these questions, what statistical analysis could be used to determine if there was a significant difference in probability ratings among the three groups?

    Question

    ApBZxU5cu/XS9eEZysSRFWqt8NH8zu6iPDpFvJlzDzEDKd4GsaV5YnbbaTjr/HYj4eq2/hkm81Y+1cwr8e5nzL2WLE7JL/kgTYg9Kvpka67MYdj4b4D2xCk59I0Gg/5vLJSS/L6AQSHVr9ZBYidY0qMPenNfoMQjUv/8A8Ytov/n8U03CAHDWzIg+dW/r2SdCLN2bgNvNJ2igNk9k7XSNdetnLo1i26pJtmsKe32dJtG3gHree7lighcJ+D+ego48C+aeQTQCHvR4W+9dV7XsqZwdNMtFzMazPA3cGGBm2Nbzh9evGx4+AmC9DLXPJy5Wzcmy0wsBlXPfezmdqTfh6o4kON9oqtjXKLE+z1UwGQHxa2TCqiqGtCmT4KrXXgyPMJ7WBE4jX/Jk7L7BkIB00UTLC5xNSmw9hsXqNCr0Yr+a/dHL3G/zd+Jx9pN2uSzk5Lq6EcPClpjGNR6dOM2t+zpD71T0cSnNFiKxF1F/Qb2yd72qCxmfQ==
    Correct! The researchers could have used a one-way within-groups ANOVA, because there is one nominal independent variable, number of messages, with three levels or groups: 20-39, 40-59, and 60-79. There is a scale dependent variable, probability rating. And participants are in each of the three groups, so it is a within-groups design.
    Actually, that’s not the correct statistical analysis. The researchers could have used a one-way within-groups ANOVA, because there is one nominal independent variable, number of messages, with three levels or groups: 20-39, 40-59, and 60-79. There is a scale dependent variable, probability rating. And participants are in each of the three groups, so it is a within-groups design.

    14.1 Activity Completed!

    Congratulations! You have completed this activity.