Chapter 8
8.1 Screen 1 of 1
Question 15
true
true
You must read each slide, and complete any questions on the slide, in sequence.
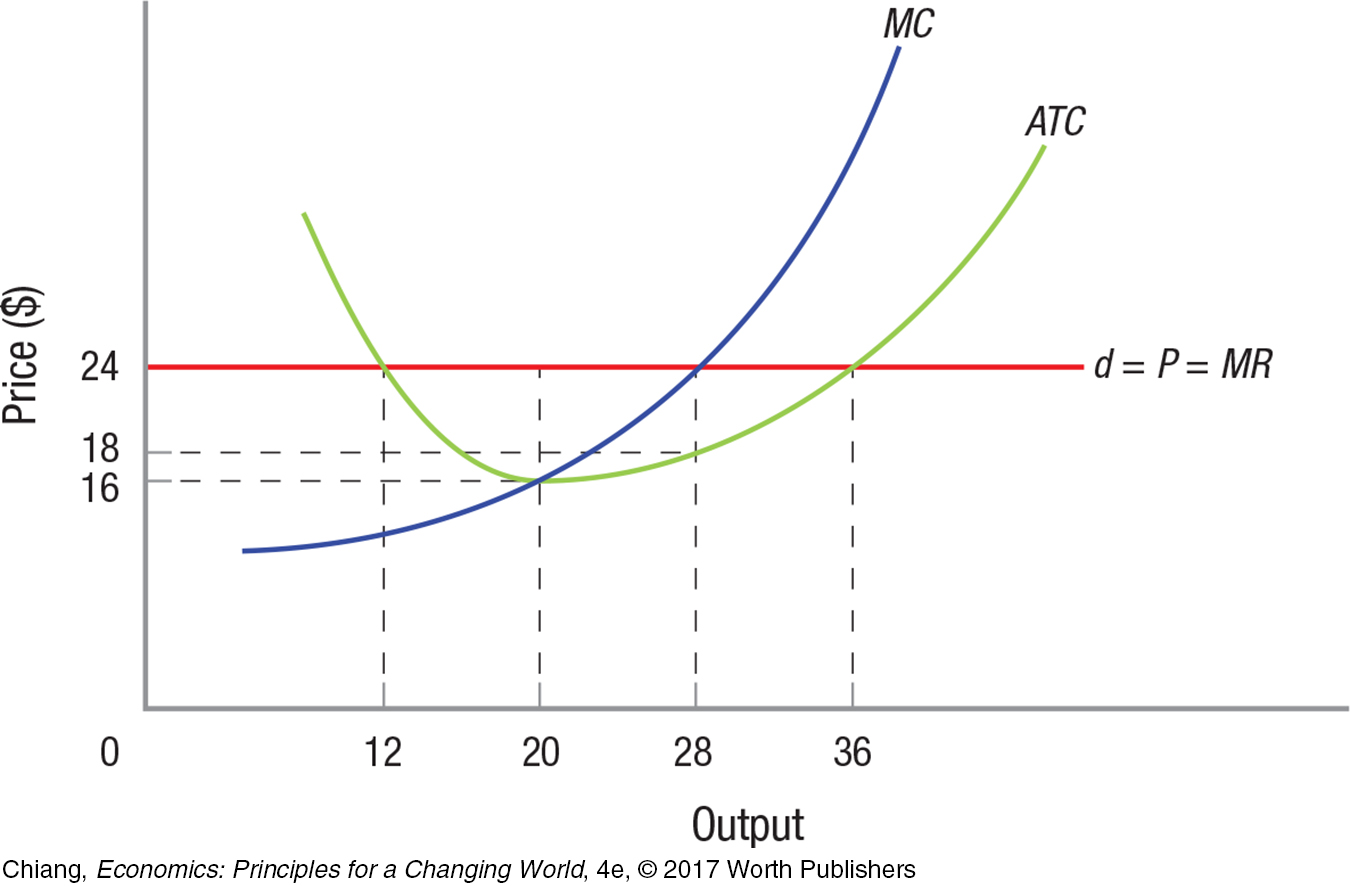
A. The accompanying graph gives the marginal cost, average total cost, and marginal revenue curves for a firm in a perfectly competitive market. What is the output that maximizes the firm’s profits?
| A. |
| B. |
| C. |
| D. |
Correct. The output at which any firm maximizes profit is where MR = MC. At this point, marginal revenue equals marginal cost, so profit cannot be increased by changing output.
Incorrect. The output at which any firm maximizes profit is where MR = MC. If output is less than this amount, profit will be increased by increasing output, so a profit-maximizing firm will produce more.
B. For this firm in a perfectly competitive market, profit is maximized where Price = $24 and output = 28. At the profit-maximizing output, total revenue is $.
At the profit-maximizing output, total cost is $.
Total revenue equals Price × Output. At the profit-maximizing output, total revenue equals $24 × 28 = $672. Total cost equals ATC x Output. At the profit-maximizing output, total cost equals $18 × 28 = $504.
C. If the firm maximizes profit, it earns $ in profit.
Profit = Total Revenue minus Total Cost. If revenue = $672 and Total Cost = $504, then profit = $672 – $504 = $168. (Alternatively, using the formula Profit = (P – ATC) × Q gives ($24 – 18) × 28 = $6 × 28 = $168.)
Profit = Total Revenue minus Total Cost. If Total Revenue = $672 and Total Cost = $504, then profit = $672 – $504 = $168. Alternatively, using the formula Profit = (P – ATC) × Q gives ($24 – 18) × 28 = $6 × 28 = $168.
The presence of profits attracts new entrants into this perfectly competitive market. This shifts the market supply curve to the right. Demand does not change but there is a movement along the market demand curve.
A rightward shift in the market supply curve results in a lower equilibrium price, all else equal.