Chapter 1. Chapter 2

Step 1

Work It Out

true

Work It Out

Chapter 2

true

You must read each slide, and complete any questions on the slide, in sequence.

Question

Here’s another specialization and exchange problem. This problem is wholly made-up, so that you won’t be able to use your intuition about the names of countries or the products to figure out the answer.

Consider the following productivity table: Which country has an absolute advantage at making rotids? At making taurons?

A table with three rows and three columns. The second and third column headers are Number of hours to make one Rotid and number of hours to make one Tauron. The second row is for Mandovia with the values of 50 in the second column and 100 in the third column. The third row is for Ducennia with the values of 150 in the second column and 200 in the third column.

GYRQ7NU824gmvQBsFc+mZkM29hwDa047 has the absolute advantage in producing rotids and GYRQ7NU824gmvQBsFc+mZkM29hwDa047 has the absolute advantage in producing taurons.

Correct! Mandovia can produce 1 rotid in 50 hours but it would take Ducennia 150 hours, so Mandovia can make a rotid using fewer resources. Likewise, Mandovia could also make one tauron using fewer resources than Ducennia.

Sorry, please make sure you consider how long it takes each country to make 1 rotid or 1 tauron. Remember, absolute advantage is the ability to produce the same good using fewer inputs than another producer. To review how to determine absolute advantage, please see the section “Comparative Advantage.”

Step 2

Question

A table with three rows and three columns. The second and third column headers are Number of hours to make one Rotid and number of hours to make one Tauron. The second row is for Mandovia with the values of 50 in the second column and 100 in the third column. The third row is for Ducennia with the values of 150 in the second column and 200 in the third column.

9WQrVZFHKVmf/vpWqNlvgn1Tg2kDyoWxvbGiphWGSAdq26MdjCyWNeWWrsTbi+q+DOOJN2IPm1p4it7p3Dpjzo2IGRDjv6jhoMKp2E151Ayjfstn/Zmc8kaetI1B+WDduEhJ0TvdlKuKGLoN4bilWAHrjWr+PN6zhCafQHq0vFgZImqyizMbo5F0C2I017XPeHrkeHyS6tKtFVZZKDmrwASil8MiEWdySDrRiJULlH3SeT5hy2Y4IgPacRSFxtYJ9TXmifdM42iz3OCVk/RDGNJazALylkBK8RsYeOuIet5m0XTUFsHsdmXmIUw86Rs0ogWxKtgP8fs1CmvM5tQdX5jw/o7f/aa3qpX+GrEdM3wOn4DtxMY6HBufObPNQ4h2rYwKKPU/IOAy3HCpTFuRJP/izz7N+oqzo1qnsyzDaVDk1l3AfpDNKxmaeK3OixggkOr92/HeqAM+R3DXRlImofVKrBdcFHoVIiBt9N8z7EE8QW/CuQLwf/5swuL3tv81N2A69ObF0Pbw09+lCmDW0nTGQrKBSPSogtIf/oQiOmNI75Qi7KrgUB7VWpmXS2AUzjHAjFoMYqt2nt1ooU/NTTnXqceYkeiiuOpGDpHHYv2uoPyPvPXdZ8zhpgfwjNZzitv9VpRnMJPicRcSb0KEHqrYoxOvAQcBCKT6OTHAyQxEpFWoiaSljiMYaAAwnBNtTJxeTUdrKstRfJFGtsCNKPZqI9IFFE0PUejsGb5AQNlHSevWuVvHrKJNW783CjcNk7gueF0tYvumwv1YGYi9np8hASQEypIqkgLUCWLPfnQnQUxV3G1zfceaJYshXvWpy2MQQbzl+KpzsY+17FMTkTCBkQFKYpUK58bF9h+BamBCmOQMWG1mAjMTxNDCcw2vD33NjmFhbYudKr+cSyEhr+50t0xEboQS7mydzxEj7C8FW9UQ4KIbey4MqbHHkJZfoXPD0h+8ECkMOyXXTUxn75ntLKRW7wUavAjx4wYzcqcQrzrm0wZHKezfb6OZfAjHyt1MZEMBh+Rti1F2U2KCwj4LVd8J7L3Im0/XOceYLik8vfbYVIy3/HLkjPY6BtdwU/cnlXFzoqEO/ZHAjoyZyqK5C2+F+S6Zl8JAyUzrMOtrYYGx21kzRcGYzjbqKku3g/fg2gc/jgnE4moFqMT+XcFxz/EaZ2jnihF2racBaSTpbNqJ+WEfkoSepxpwxkjFQcJglZDN+7+bUosuebDmcX69woLFYHKIYaSCqGfCrUGniNck7WtJCN5r8DMzEIOIoR35APMHZIxGvkI6D62eOWThdclaYXjfAPrSKwI7GBa5ozZiuUT4K1NGM+4quY2Lt+KibvMQx9l9NY4YmMXHBzH6kjaaoKGA6gJDFXA7389x7uFoOaRsl50tWHgtcn3F9ruTYkTx/YkReHIxc5qBdpxlgFs9hQP/+tMTq4qPBv3hh+dtjl9h44xrVAFSPCUAV4GwCEQDxvNMFGFtZdQA4gRz2e3cr+N66Ud7dV8vzmZO5jZ8JOo8nR+MDxjOfKUEWyi8krgYHeTL2Pwp8nnG1mknvOyEQ3PrzLGWJ94CZk0hp4apQnDwcEdGBwqr3+4Y1X+qByn4pN27BzYChfgQWAQzzOfAtsUjZf5N35Cufrg7JZeTb5VdBEN43+fXrWfvw+SWP348qi8u6rsAPbgxIn4GEMf01wQYEVnyFxFKGgArccCMrhOQmHqwZEqYDIxUWowJcr9BddbPo9qQY+PLi5hV/HeViSBfFuunNRXh5Q2xrGrPGeJhIVzQIf2LYdJJZWdsoLHy+mP4SkrbRUJ1YyWbO/JrhkKIVUjbW/vRKPjdP2Eh5UPp2yeDO1klgwrm/o2hGz9L2iAjYVZYj0TEy/pNQ/VuGy6gcJf9C+Fulz6y7iK9SREtjdjNqkZfBM2FcfChT0y1zFnen7EmK8mx0a/Zr57nV1Aqgp/d0h/pq+kkh3XUIRDnKtgVPExBcRZXEOeBYYb2CXseJVmV/4ePoni3jNShSFbq8lpHcPTakLOQ8Ig9qclrLNQcZw+M6OXqve+V0uNTaVfZT77ktsAzmY/5/IFf8lZqGOf5AgC7JiC6r54KDcPQdPDf5cIrBShDnrWddzaN/g/IL3ud0RX5HFiMnUcQ39idY6jODve+stpZMP5yvmSBbKU01d80NivSFB7b0ngjaUyveaODLzKmI1wwOJIDizWlG7dTU0rIOj/sHL8ysP4EdTG+IZxuMws1xxN4Uw3Pos4n2LQrBmwt/qndlM1ocyWohV47NLhAHcIEmDd36ROKOnFyc6/j9/MwQV8xaevEY4SYmTHiWiB5cDta5D3/qMcj7jsbAf2k7J0mvQ586tH4+PDOoTq/16unyoke4kZLSz9sD5O9R6G72YK0e611ol7nVRqaDGD9QyhhquX3Q/y1qDjrk3NIKL3xQcdjj6tBNhRicKIdAvkgsL30JoL2yWuGQ4CEuls83T0MswOe2dZC5JSeB+wb9HV3mvcsaf4ixQ92bB11uB7XewEYmQ2aazw2flnZWESP8Eu8jQkPmjSmnjGUCUVRGZ/jh5kaRA0ua3IESMUmIR9DWHy5Dc4boW8TY5xF7a86mHbNfkBMYmWhwpsruHh9se/YpFHu+A925/i905drxM21+dLtEZYWTVIECatEHi8jOgH5yfvFI0jrBnXTUkbONmLJaS/avb9haXpAEZ15Kf/EG4rdGeXiQQ9DfGZIalTiblANR3iBMe8l7cMNQxI9NchfEDcj5eFdouQS6iBbqYgeBKGEOwjIuC8VKZF4p2pa5EhMvQaPyJawQqFQfCeKGYhS7kDO5vovSPMT+Fdt3O0i1FWELAronHF2MTBPOCfNigtXkahfepDNo6ZtS5/4B6G0e/A1kEl8NgwcCn9HjjUAATHOGZ5Xt4MbRAU6a2npUo4mY+PBHfk81fKMMnTHsEQtIZ8wFdxiEkG1DHAWdRTPyzJ3v7NhbQFj511egQgUUyVZTk5V4OSrbYymL4/8/TeVAqNkEArQUWnMhH1wHiYm2EKqqfVo0Si9x5vuOveTcYnre2ppOiTPdlnGftbo+DuP0HMa9t9kSoO4R/QkhLgiUhG6HVlbJubtXIxo+qxD90CmwSlE1P6Gq50Es6/IEqDEd30nJoEgZuPi+GvK3o2j+zB6KlKmex92piEf0s44kucdj8ZQPvmVW8dw3MxOD8tpd0oZ9ou/MGeEe6/0chwLM2nQzz/1ihNLzsQzl4b44GJhdkG1drcIUL+8j9K7SQP6DPjOc/F7+8vjW7ZQs3y7kE179s5lXDSd5EyRv1e4rlHZ3/BBM2BrlCvEi7TVIYJ+Qwq/6nhfT0Vs2c/Efc+ZiemPVbdeTe5FIGxjFGUutwITB53eFWBPnPCp8/x6u65jOdV0yVWzMQLRDTll/tJG34oJbZGc3sHIjisJEeaKghqpLKxYzrJO7RuG8yEdE1YHOCnTYZHSN4rVN6vA2dU3AjNnEK6UKEoJiHMGviltOBhGfeMQzc0HCv51QFPBUeCf5ffyVP2ZXhUoJbKNEjlhMvqlmygV21QmeK3YWLuVUySmq+d7MRO6xQipeK8hDgiLjL0hEwKainWd/Cpt9+96xop+qSFKcxUsEvwBLNHZnvijXQkyK/7yGqfXVoIV0qevwzTRu/7go/zUqy+awZXIajx27Zs7g7LbKTG7dCOU2v46ju4rEa8Pfw/8uzL3KVDjGDbgBW2BoFoqjOiQtP6LskEju/aXCugrworKfXk5P9Pw0/eqgF9eHQImwOxuwbqyxUPay/k2b3F9qSPQRezHSJqt7Ah6OzgkuJEJKFvE+tzFk0ixJcqGnf9JbkOPvTaJKUEeRg==

3:00

Step 3

Question

Based on your relative opportunity cost calculations, Mandovia has the comparative advantage in producing vb9A9e4Lzm2K6pGGjuv1r+iYorY= and Ducennia has the comparative advantage in making SchntS6vbu0PmBzvRiykPLAyozA=.

Correct! Mandovia’s opportunity cost of producing 1 rotid is 1/2 of a tauron while in Ducennia the opportunity cost of 1 rotid is 3/4 of a tauron. Likewise, Mandovia’s opportunity cost of producing 1 tauron is 2 rotids, while in Ducennia the opportunity cost of 1 tauron is 4/3 rotids.

Sorry, please make sure you thinking about comparative advantage and not absolute advantage. Remember, comparative advantage is the ability to produce at a lower opportunity cost compared to another producer. To review how to determine absolute advantage, please see the section “Comparative Advantage.”

Step 4

Question

One billion hours of labor are available for making products in Mandovia, and 2 billion hours of labor are available for making products in Ducennia. In a no-trade world, let’s assume that half  the labor in each country is used to make each product. (In a semester-long international trade course, you’d build a bigger model that would determine just how the workers are divided up according to the forces of supply and demand.)

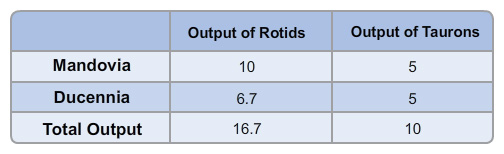
Fill in a value for each letter in the table by completing the following statements. Enter 1,000,000 as 1; 2,300,000 as 2.3, and so on. Round numbers to one decimal place.

	Output of Rotids	Output of Taurons
Mandovia	oZI9zh14cXqi/yhvMX+1w8eUGbdDoWk8	oTr4GFJmXRqi7w4qHG2Qf3G5pqY=
Ducennia	nEo0Hz9nobX4JflhG2hd98vtSpB9zVfW	oTr4GFJmXRqi7w4qHG2Qf3G5pqY=
Total output	+ca9UHjM8DZ02WjfMb6daN44XQAqUj7t	oZI9zh14cXqi/yhvMX+1w8eUGbdDoWk8

Table

Sorry! Think about how much each country can produce by itself given the amount of resources they own. If Mandovia equally splits 1 billion hours between the two products, then how much of each would it produce given how long it takes to produce 1 unit of each? To review how to calculate overall production, please see the section “Comparative Advantage.”

3:05

Step 5

Question

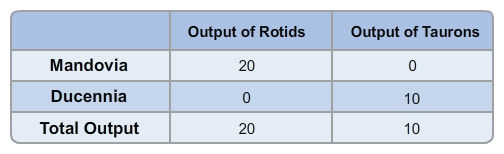
Now allow specialization. If each country completely specializes in the product for which it holds the comparative advantage, total output of rotids would be Tu9IG1n3UyE= and total output of taurons would be Pz2PEfhsNWI=. Enter 1,000,000 as 1; 2,300,000 as 2.3, and so on, rounding to one decimal place. The total output of each product is VTd5VKUscpoVGkH50Jd5CQ== than before.

Sorry! Think about how much each country can produce by itself given the amount of resources they own. If Mandovia has 1 billion hours to use, then how much could it produce of the product in which it has a comparative advantage? To review how to calculate overall production under complete specialization, please see the section “Comparative Advantage.”

Step 6

Question

Finally, let’s open up trade. Trade has to make both sides better off to occur (or at least no worse off), and in this problem, as in most negotiations, there is more than one price that can make both sides better off (think about haggling over the price of a car or a house). Let’s  pick out a case that makes one side better off and leaves the other side just as well -off as in a no-trade world. The price  both sides agree to is 3 rotids for 2 taurons. Ship 5 million taurons in one direction, and 7.5 million rotids in the other direction. You’ll have to figure out on your own which way the trade flows. In the following table, calculate the amount that each country gets to consume. Which country is better off under this set of prices? Which one is exactly as well off as before?

Fill in a value for each letter in the table by completing the following statements. Round numbers to one decimal place where necessary.

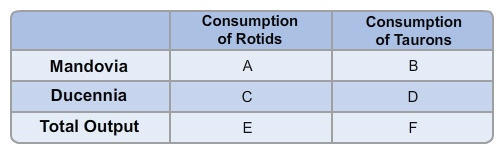
A table with four rows and three columns. The second and third column headers are Consumption of Rotids and Consumption of Tauron. The second row is for Mandovia with the consumption of A in the second column and B in the third column. The third row is for Ducennia with the consumption of C in the second column and D in the third column. The fourth row is the total output with the consumption of E in the second column and F in the third column.

Mandovia would consume A = KDcUqOYoaQA= million rotids and B = DYU2tVvtzEQ= million taurons while Ducennia would consume C = k3jMG2T1npQ= million rotids and D = DYU2tVvtzEQ= million taurons. Mandovia is h/bF7OaaJqGzjNzY/vsU1ma2U9WzvDnBlxGgRDii0ukqW1m6hJidkWN1g6g=, while Ducennia is h/bF7OaaJqGzjNzY/vsU1ma2U9WzvDnBlxGgRDii0ukqW1m6hJidkWN1g6g= under these prices.

Correct! Mandovia will consume 12.5 million rotids after giving Ducennia 7.5 million rotids. Ducennia will consume 15 million taurons after giving Mandovia 5 million taurons. Ducennia can make 0 rotids and 2,000,000,000 / 200 = 20 million taurons under complete specialization. Together, with trade, they can consume 20 million rotids and 20 million taurons. Both countries are better off than before but Ducennia gains more at these prices.

Sorry! Think about how much each country has left after it gives the required amount of the product that they produce to the other country. To review how to calculate overall production under complete specialization, please see the section “Comparative Advantage.”

3:16

Step 7

Question

This time, the trade negotiations turn out differently: It’s 2 rotids for 1 tauron. Have the correct country ship 10 million rotids, have the other send 5 million taurons, and fill out the table. One way to make sure you haven’t made a mistake is to make sure that “total consumption” is equal to the “total output” from Question 4 of 7. We can’t create rotids and taurons out of thin air! Are both countries better off than if there were no trade? Which country likes this trade deal better than the deal from Question 6?

Fill in a value for each letter in the table by completing the following statements.

Mandovia would consume A = Pz2PEfhsNWI= million rotids and B = DYU2tVvtzEQ= million taurons while Ducennia would consume C = Pz2PEfhsNWI= million rotids and D = DYU2tVvtzEQ= million taurons. Mandovia is Iz9qSGHltVsKOtJzLslwcYRiytlY9zwa0pUAd0H3I2mZid4ENk/EEgXoF8g= while Ducennia h/bF7OaaJqGzjNzY/vsU1ma2U9WzvDnBlxGgRDii0ukqW1m6hJidkWN1g6g= under these prices.

Correct! Mandovia will consume 10 million rotids after giving Ducennia 10 million rotids. Ducennia will consume 15 million taurons after giving Mandovia 5 million taurons. Together, with trade, they can consume 20 million rotids and 20 million taurons. Mandovia consumes that same amount as before trade but Ducennia gains at these prices compared to the prices in Question 6.