Chapter 4. Chapter 4
Step 1
Work It Out
Chapter 4
true
true
You must read each slide, and complete any questions on the slide, in sequence.
Question
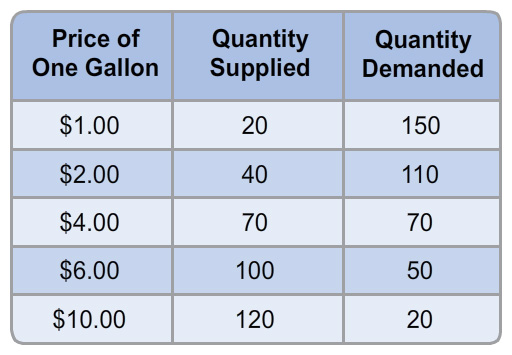
Consider the following supply and demand table for milk.
Step 2
Question
Y0S8JWQSLWCJHoW3BtJ81g08hcYw1uvWiNTvvY8+gwoePaIZXg4h/20TVOIBc0TPGwfVlqtxyfrGuVvmt64AuqTcowFPV3VZskF+2kAYXJw9FRLe1GcsOJom8ImCzmQYLMjfE68vGFpT57D6MHJhX86mnuJO75eSLoS3923AjnQ5glM4ATD9Y1wIZjawl111iHRhkG9ZsAqNRFsXdviqiyGl/JwRsQxzbHSMlFePAuRTejVnPof3LPtbCPQhQwYYAlK9NWng3Q6CTV+RSE36nXe0+QppUCRh89K6CSE3GeA1X0tBI1NGHpTHjhUHU4jHIsfFXptW3G7VswkHIYT6vM+mJHKELXcNTEXC4oT9dBtmXJXMILFi1rCURWXRhf+8xysz1uZ31vHGM6R7PupdscwU/z/PSsoRAiV7TXKX/ximXMjJAhsl39PG/o8/sAC9SSFkOstYJmeVFYkVUR+lwMAfCNx/xP5wuXFSKs/FInGeetHRHRmiPAR88ki5IRriTPQ/dnf2+xFKMTSpH4DKpS/GfMPdB2pEy8lrzkH687rl4fP7RBBlzRrPCmHdKDoovuV83WPSYhvmVQ3U7Deszve6Qkg5/+dxqt+3AKz3NSHf1PnfjzS1k7gMUSNkFyDtue3uQ2WFyv7Ayz5y0qNTv/+/2hY6DAlq9jZ8/ReJTAPje0X8LmFBBcxvHc+vQLEDQDzVl6QC3sMPguDfKIj7HhvnEAOJ0Fh8fLYOSgmWthEBNLOE1/zRnXkK16A7vevlZor3R/LsD6J2D3ewuTJFIQAZtjE28+g/5KQyeISXfd4KPOP1xkB9Too/2pWZsNN6rE9EYWn12cDWSMyRMFsAzQOzLq423uohF+DRyrdSRAi+mgD9EoXd7+MdiU6aejzCjIQv/C6BUWnFcE3moTdZh5ha7jpP87GrCnLRfo3FUqjeb65ONEqFETaE5vXkNpg0OakHCmmRGaz2QWcegoBkncQ42CTVn4jiHJ3klgD5oTnizw1vR3h9IlJAsHvXQMP3bHciFPGGjasZ2KWv3o9QkpFP2RDGZzmwreIA3+5NfZtDutNUiQKiiv/QSGbVIRB5BK3Gag8e1QpeeYQd/9kRAhpCNQGEHwZbRNbtpZJdjhCw86DYpEBTCqKOcu8eLKJxQN5CMqrgyu48A6eFB40ifEHf97MzreT5vEuOezfVgLI0nArobmJ0UhJ5OwU+OoAqjyjvPf6oWWbf2ONE2QnnYRbj+vxV1lbRmYpAAI2hbWg5aCDa3fR6M9RVrmB+UfwG+QlWRF+/h/AEgr9riQmwZQPkXGCh+ADDUSgvVVm0uo2k41pRpZoI8Bf+0e1cJJ3+r4K+W8qj/MPlkwzwkEg9EoUQSbY1vr4TOM7Qj5MXxM4CZnwxeC/12x2YYOir82fpvQ9te7VDNzJdiHw1HfLiHFMKZgvfUi/T4A/d+4YK0FtxH6RINCuDAbi0GiQDNfu79lND+K3OPo/5hAXib9LEdlZc3pjxQLqZaYwg1j+8bQwm+FZE55GjgjNlujnlaidxypqUkpRNGhjQ+KZTCkF/wqvfsQd3iPtOe+2l2NEuJNGOkxrPYDxDaZPd3OUnjfagHkUCgyOhJYyqiwJmjwCyAL5AR3ldESY/P4l10oqbDwBflkPVR6GqyURcYyFQnDuOGddPkcH8OhAIfjwWrQMwF9PLtLaM7VU6WdP45L9zfNycCtKIZw1EGW7DlzsewAYC++QxMS3wP3NeTGFpNiVaa0wCh7WmvRdBWSe3LbI9ZDY5cY+uiw11gsZCgoiREXmCnwYWJjfQ0IrG4lEEtXrDJPNokNfZyXxx2meatO0XjwDvRSZRS9iWe9natrwoWr/VqJngQrDfp+7Ih3Ddo51d0yR/tLcWHfbkIsUBcvryWedHptSkefHYLm4Fi0jRY56TeRoawxldMHJo/j9IDRCTaBbFPmc7ummavKVJU938igtgl6IylIb/h8x71AbtJ3fNi1ojcAjtHpOlYWz9rglP4lH0V8fCT4B47gnJmsfzHxP88jMZQ+dfIFP4yrDOhZ/L+WM0B0HEOENUonTWIk/dWZbMOIeX7epzCISws8R1wqXSrpJx/azgrozicIgzMcse1UUIMnCHVARyY6iYYOVSGd+FjWq8o/giWn0DrIUUjURQQkczHkpf27169hphc1GkRpDB3CHqR+4ZWlc7ocgUB7E/xAi4raGKAzbJv5H2oe59qD3lhqjiNhsQS6iuq9bZ4GyVWPStUnz97OYaHsOrp8/DQepakjOzz0d7JLL/yxQ3NywFx/8Z1wrdeZ97bW0QgEMKZLuOnborbfySex11kTq0r9/a6yVKXHf71DSQQsYtyT50prA5zr8ovpR+/KqLZAdCY5GY1dGvk/2H36qkBLzdvLazAIHIGDlQSE3RRhjvjfsdcBezh5VfKXA4ydyusniVBhj5+bNU3V7HczcLKey/Nd+LuhnvCu3yC4YHSgbJNZZRgauRFRyW6rWclRigTjUTATxNeQUp0X107sC0EIJSw7//5dF+wO92iYHiy8y5yPHKVcpd2oWY8O7akumi64vsYyUIPfosvFLDnthEgiea5zIFIangvFKIhR7I/3IxzGcjlp7H7zmVj69afPLERi5df219Q04dy3Ml/EjUkPZEXEGxTnUN50kqf84EtQ9+KclMAwtGJd7a9Ffbq3ZLnSHp2SCJr98HLX1E+JFqKpHqkJvhPybWd3KUqEpSMTIQXSMechAJoNYXfsUH6o9oGHXdftDZt87mWcGNbDYI3vcO/nBVRlpNXsvaXI5jIk/Yh4HgfqPr7O1E5n5Pirrh9ilB6ZMdxL+JTD3t16FY+8xTs4mXjqKTqCNKXBckL09Rrlex5e3Oy6oDqEil0tQiI44v5ppD24NDIZrXBqxC3N1Z2F1rXQxo8346jpw+jTCbssByFuJMj9KiHp2SN1ci85se/t3112aDBRgUN7K5sNpfRrTlE/c92IfhuLOePKk1frU5zGUHtiz6VAWeJj2WkV0w4tLcvQysj8OJ9pq9FaCK0lkNJphUrIrwM9fTmsarhueecc00JoupTF7ttWwOsDwDBXpL32Ag0eeNZmWqtqtHBlDc20JH6r2P93NaRV97j5mXevSVQ1+H+9TJdLWkQPLBGyOi1XWVi6bmPQUKVBAvRWtkaY2/wCPODOenS7OCzzGA3TGkQFb1a8y9f3PFy+VCsOwREFDWy4kbeXiZK/t2Tl+Va+XcPzRaqTf5vz4bYe32E4k/7U8mEuidwKW+e1IMyxwGQ0G1HY2blPPKbw5Ovhhlx0VBb2M3SpwdpK3+8Com0ZdyeVmavzyvJhSb/i4Mgo48FbPYUFSsI0RQ21Wxygwbi80XB0o58n2EVyBRpGft8lvEGnvli48H1GwnoM/3a+VCBo0zHo+JxJWm4FoiLZMb5+Pwall22gyFX1BB9zmMaInj5lNkiJQk88VYQTbNuY3fAwY1G/A59T+EIiPt38Ij4eV7JKSdRp7GDtfeMHwUXWBLvbrXX4JC5JCd7VzwuYK3QFdYFwNcrs8yr9AhmnY/OxgxQQcEHUcC5qBROsudx9tnrghZt5SPOnv8M1yty0AlsYfXN/zfROA8lh9K/JhI63rbrf4xlmG1hghK9JoYDoTiQfUeoNRSsFn4CzK3EBnAItrMJ0iAVt37xUBIEo9gnOOj9vQSTDWd+lh4bK4iqdIFAqvF9ubIOnjPflUxPrFaScA2yEmlfZNvW2Rmz5XQHJbbQw+POzeIGyuDcYywXX+z7oF6d8f5rCWyQoneROubhvmXNOCKebeuOE832qK2SEh9pCG+GvPRej/HhXU8mVy1ID6CaYxQPswSxQ0ciigP/C/m2lGTt6LPJ1m1wlZn/SUS7rp6pdn+J7nOrg/40HHL00klU4FAEbKpbHHet8RfAaCG7ljCqT2gRYH3OAkyE5N+W1SyXeyPQmO0KDQlQRuzodlxQYwAagJCM8euVqCewghgkLhVaxqXzO1kU67NPoZoE1vD5h7vOPY4lGSIMrIQ0scoAyaV+IXMxEvmdoQ+xWMoKjg4Q9ccfPrM18KEnfvImLZBEigV9zX/sOe7ROJo8u2EkaUKHOmfZICd3v/HhDNCRy2wFQujMkqa6GXGb7VaDCpP0aN8nT2kD9jg0AQ7tj2XxSW8VSnJjnk9VN6IZTklM+LHPu1yngbxEI+t+/XOS0bK53wpHJnW0l7t8Mt2MDjUrc2GXC8lkl7f/E4CtkzDrB38HSJzXyCDeS66tojMJ3FD0NZvn4hrnTB+SdETwE3Q2OCkkZD0GV67wdGyNGgYMJp5uOmU2hQq2RPwrXAdfZ3dbMfe/+4ljzcJTLwkYCd3abSqZflBtdMcwBFzPA4USzl5PsdsArPCi3crA5AunOGL7S/0l8YvkorhZe7A2G/Lc9LPflgkR+rbtGjgALVAEN7ksF/9OPhUAqCdAlA0GHuUKvqckyB7Gud5QXnuvwr3lwr54pJfVS0ClPPc3weEEv3KNJ4eymx19zM2OK4ZUaf3Sp2sggzyiLt03grAwk4+QuRJFzd5adE0Q9FcjhBFSGm+cVaSekgSdAM6EVos0ytR3fO7hvWZqQ2hYmGd3TV13zudI3r3e8xrrXVXPeA4YTEZvxfxlNZOStkiJ0i+HFF+YRTjE/Q0jSDN1cjsgBPnq2TWzBcHy7pi1qbdxreengech+mbzfYtyddYQ13/xiI8r/+1ue+TkY3F6eq6qQaQKVd8pIdlKYOY50PJWnZgO2fTrOTdRVmQqo7Iy14VxeDo89nR/bwpQg/utPMonk8yF6hcWkQo0yxx476UjxeSkCrj6WlPISQKHL4gVP1Nhk4a9UlTXqndN9mslqLbv5i0R9XENJmYYNqokX5l6fno5IB4uZnbs27TdYfu118h8m7j++iWAkLoyNScDRvW1LnybGhqer/x1BpZ187vj08tV+tIZbjiO8wt8iK9TAO5D1+iyTSCkiyX6B9lj59bpFebchsL5fcR3V/l+PV6qxmRH3yQ3XkCU2ppwGsJSuv/1KnK2LUTQ9koghkndWx2v+ca+P77rmc3I+pTLVa4gpSQ/VKEfFvoRERPRgml/G8k6r8dyCRcwA72RYL8JZgMz9sPBvHsMCiP4YsjO9GoGcitwPdzXlL5GNRWDbmvmMLPrFDt/KGUTnByFBA/30rulcuSOVLMelJjFS/gcJ56TE1TlQHqtnDLV6ZOaVRXC5wXrYj9pnIxYphwRMOrChDnbd6zspN4IVXOQ9dPhqBYkQ+CJ2aW86HCh5MXYbwMx+r0dwKdAtqnWXd6mjjwAVodYM/4jo7z2UBZH4hta4BBiVPHVmSDHuyEF/Xe4XHLR+3vudlPGO5/q2iBh0CkwD211x54R2WDf1QKQ4ZGA6ONLbu3mUtMZD1w0r17dt07+IPE1RjCmHGmYZgBd/5sJECAhV9WFSouuWuNwThbW/cC6D3pECXEnpVsbuJ/eSS8UW2bUThhW2Bk2f63UHHnfvEhmi/nhsctusNz5m0MOcjYWkZo54naM44OZbMXi7pb75V5O+UeNfz5GFazBsaSeeZmfKWXREB4ezLzwkJMnw8h4M/h4rboXHwHThWReM3DkyJ5s3hphThxiur6kb2Rl3GNu3+D97LkEfG6uUnqqgP0VrjaUNQST6+Hpwor9kMTEzivtaoDphCbwNpzwaZ3xy+YtcT/xI3LQekMh0nGruB6s+l3OP80piAWrHjHx/Qm4NZLRk/65PnN65i7BOnUACFMOtFkj/O/o8VX9AHy3oGM1aQipFb81q5HTB54HRtuI/kdhrnaqrIl+HFASSiHJm2vXdjmhc8dYLNoqy+YLflUqRro1HZLytZG6wUtRAdZ8k39uQohp5HU9HwUOB3MyrLZUASoDdXaYrv5E8nf6SNR6x4jDtGxz8gnS0DXSdAYYIvxFQ3vBIu27xdRQYlWL16TFz8h4UupGS9OgapddHuX2MuhlTVTCHQ828Mtbtjej8Ugr59ojWEUdJfmd4MHDKwGc89+JGxpZsZXGBjDEZBjb3XJENYbWBZ8dQ5ljXsfftH2BaFyYeto1rFjoccgpEkYS0VJZyD82S4w+bxZtPGdUPe9fpognUH6AHSFx9OPK2OCSEqncuKkd/2/FszHitErP+D/pPsHPwHaLIVXrqODnu9PJmjD1R3xbfzJNSj/tOEz54LmkZ38Xf5EVwE6y8DWHJh/YGt+mJoJ7d+ELJLQWtzO0FCxG6yyA4HuJAfCrcjfaw21RpBHTcS7qKCLTM6g31fFOiUmRHObmPNPV3h34cbIv+2OVvKZNLOEKSlhbm53VlIwT/u/jTRfsF+Pi6gIpLfAEPb+48eS/syFq5jznOyRB4wUlOPeO+zoHXTSAq3jOh1G5Dp4zMIClWzIKKF+gy7XdXebvbLrKNP5iHRUEWlnK5VxIhzPL2uEYoqrElGSqJFqOjtLigIcYhBLOSrsHpH/Tjamz5Fk125gmEODkmD+pYAVFvvwsfUx5o27sjs2WgFDdnuIYbsX/CoLX00Oj6ScBbnX32oAT591go7a9M64eGZN0vB0fLoBOiTh36y3MYQPagKuAGbBaCAie02hbvzn31ntWFhe/hNcbxjLwSL2nEBmc0GEUOZsrrOeaRwAOc1c8kVct3LqMDfW3XhZUgirkubcn1EMz4qG/4anXht6iKFdTsV14xntlhUagQTBTbGXm3aSgYfx8c03Hzk9hkWOMg4wrpZl80umAhDEofP+MSkNmopRFSRhDWopClFWl/N3fnTtJ8DNjfg/1Do1KpVRWz8JI4TKkUgAeWiGh64/+OAlwEXOrw7Deod/J4RaF0IX1RFipKMLZDhjbNLjdv7KjBCtCs8Rh72Wmt8KtBod0OdyqyT4kiklc6SJ/pXh8Z1+ilHntIrX1k+d5cjnL+Llt+MA7WheoIf/SYFer9bBSOxaKmQnTD0hFNGmdYWmZ5bMACyOBuDhnc2E/qt0cshUQRIyK0M62tvsb1D5gL6JKbNIBrdsS1j37cwyk7WWDpSp4cplS26MFv184qNYhR8RsKp7B3vKQWqvkaIqU8QBRzrC08Jiar7Hhfvbg1FPDgc0Kwvlo7XNs5A279MsAgOEyD9YSWSr+mU1PltnfV/ZpjdKx2s3cwhhfOcrNJlMB08njzpCuUaEVCgvJeKD3P7ex+TlBOaIPwxORKfWvZ3hfDuIHkH0ZswqkU8v7OnTU8W/TGDL/lVDSkjMl6FcfzjZ0f8keijmqHNEz+83yNbzd5Ga5948OJBm6CIlcePNLoyl3sULVvphdy1UmwLOh/JePTR7Jvyt8WpNNAmofNtiKppAn42X1zMIUe+vNCh5bpdWCsZdWG2o1ujXPdSWAgrABUtqn/5BTr4MYKxx5YoB2lTltj3lojtaEcNnSBctPu6U+uNBtLjLd7/OUHLSUawq4y+zrvHrL8zzJBDzRA5SQ5eUN1FJdflh8MqZjtJ4cXiuBKn8tDgG9mmDSveyO+x8yC4q3Aq3zAaxO9PUrD08UW4etsKHeRpJ+H9EY+Y8j7WOc4P6UiT7fFKN5sbH66Pm5hpPht6QeF5TJfm2FSa4QED2hWrec7mI2zWzt++fn0rh2M/jX28PU5W0rLxt8Gy8Jlgftj/Afudd4/ZRt36IOQSkU5+9DczeiaIzWFqiywx1XU6SPTHilHlNjohYTaKuP/mtBxC6fdR3bIsiC3Fv5alzRvcSBZglxXUYsnpOZS5nSUG9EuxV7j4o/VS/QCfnOJ3b0SMfe5kcYLge5UPaRfQitIBN+3C7UbRzQHnp3+Vyx9pqDkGvqiGRz6qqDPgenxMz9Um0ITv1A9RxQpbnEMi0wacnyCzFfVoENcVsyR3fdi/GSEIUubTIfwMSsp16yPtje12wKe5QPHJksePRY+n2QgD/JJQUFXKEvyw6wLRFtyzLTAuKcG3syZGnKTQVRWfAnGSrrzFl+WoGJEmoIBKA2NPUbwJE5AU6yA3/I1wuHynZam5z6wt6MiG90BhrFfv7XSmP+7nfZQ==3:31