Chapter 5. Chapter 5
Step 1
Work It Out
Chapter 5
true
true
You must read each slide, and complete any questions on the slide, in sequence.
Question
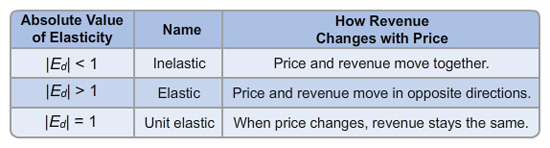
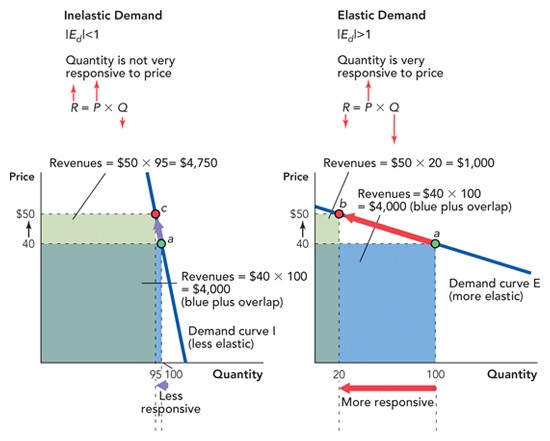
The figures above both set out some important but tedious rules. For each of the following cases, state whether the demand curve is relatively steep or flat and whether a fall in price will raise total revenue or lower it. In this case, note that we present the elasticity in terms of its absolute value.
BdZqHcIiEW1SRC0l7nl3z7LtfNvtGENoqj8urndsUBSzsIZiPmu95bZa+mHA3++lz2ttMqF1PjMEbcGL6vos/bGvPmxdeMkqvJI5ITy02hDepQ5eZgWfT+3af7T2b9cRWObm8o/5osCNa3rYqntPWCi5AuqhecuAfAQxGQBby9EdeGrr3+dDcd9ox+iODAaVNn8ZDzvTTfIIX2h/gxLN4WyWKZjHXno1bWJftGVVMaYwPh/vXDylYhOqDVhlSGZMpC2xPi8Gh9cr54WhB3MueJGSAwjie/GV99s0SDhPBA8JRO+jyXGOfrWIH75BuyutpR70YtysCbNLCvhgMWhySgAjH/vbVgsM4kQzGEf78/IQz5iGBPknRGcLl0yo6ShNmS8j3s4cRUtX1dElijVT9H4/y+fn2Vt6a/Br+FKrj8l3SvWEQCRymkR7ICfixKbugEm3jSCW6wSPdZVoPGXgj+Wj4U1ACH4GTXopIHiLDNrj1T+lndeJdg/8Kno4vPdiuzW+l4UDGB6AhmE0cfKXHRljBgHlnN5ZYDrnmFRjEvCn/gKWWv4YGFrz//El1gRA/grhBEMnBUG9OL/qOOvPs9fP7BxUZG6GT+YxZNEb5P29OhgUJHViTzz8xlmrfgpDKA2qTG2rBkNJitZK+9tq1CzDKtmjIWU1E+hdsrh/hW765aOqprH9/tZ3gwkvArE40F16plUM2iV91hO6MkR9/HOSMQxkdEjIhEdHDSG+UuY3QTolwznUTVwa7kbX3vXnkhFBXbxRZROYnznxoM4ydoDQwbisOcHdoXZ9svCwEgv1HO64csVrtxLhsskg7IchFlYkl+IeCnEirjAlnITlW2EPYWXi2ejx+wvulnFMn5VWf2mqTheovw0TxX4JOb8C2+JOclCym2wEKWffBTx01MUVgd8NwyWLwyA5IOyV9N2Xs7lhxscXLwwBCzKGpiSZT+DS0tJXdMIvHNVHaK3MjautHUqFDoCcVlkpweMaEJvLPERi6nE3Mc4dS1+l1Q+t7U78rgGz2Wh68QrxnnEsWGy5UO+PvS/axYstSiUDpOW9oCBXj7mEfTyogwqLBNmFEkClgg3Z2N5/9ieo+TRHTp65LnN+YVkT8B8zs+gC7cljU/tQqNfKl3NHwH8kyHy+DSg3trIIE3SCBea+98HiUEsgY4tbN/uDa23fBjhiJ3crm33a9eUqNubYOaNtNxUDICF3vPokzATT7jUO6z/zCT/dT4m/gT2lsVNB9xrj11b5IHnF2QjdpVW0lGbwpXBJ0+wvzXwn6/xc6fXU6WbtwFdl34ZGnAbTr3lvmVDJfcKVoaXhZgYRy/6eD/3CODfT4n1RAhgj5hYhw+mi10lZFBIF9ikRLaQUmP4BXuWLbkGu0+Yk6ewJ/pB7+s0hCDCukcKjqVrs1uloPXbVxzy+kKtWut/9nWzieg10v8OFrSoLovB/PV32KW75Y3Gy1FPNfKqFzi3V06fDJ8w0Y1oNwlLIIxpN/dQlGbGn92r/vXQGI5/Hba6KmLc5W2J8d/yC8BbN1uoCJECNAZP1BdiiacxlhjYNfCgR/xYIOFsBY++FGqmD+W6vPQ2iecdbW08rfilg/udKrYUQtczjZNgqGGDvsiDmXFQXOzbUO1hlK3ht0/P7dIHTikLEEUIaCv1+c3C+IHXH28CVBlkRwU0HVYe7B1aK+Mpaw6/jMsVIGLHu9SOwSMxowfP+9jxUqUW5n1IStvVa8ptMF2U7CASKR8P1D3ZDwtCc3WyctKKidPPbfHQQyna3F99nTkUCMOKHy+srHUfnT4wvxG142sHksbVF6rqrYyIQj8XJXHMoJepm8ly+RAFqWO1HtvFgsRHCZRiypuJQwOeBuRWH9DHUWZ/mDYLReqdq1VLAe0G8OZdG+vag0gsqZ/YK5z8I4M0FKnfbHzJoogRSsRnB9y/mPrkMbTxR0H3VI5hMiiqto95WNisRlvo66JXene0IJRM8R9PmHgN7X5t8mVwE19AuEfSZywdZ0TEp5nZyAToWFxonISajd2yTShrIH5S7kJI/YbRxBEYCd7fAlloSZr44CmAHSUxMeMsAw2QfKrVoqhhPeLp5g9VVrvqaWwgpQFoB0b7Q+1XfueZfP2eL5uOBcB6mihbtpnxvPCQibXA7OiN/ceov04dExpPufp87TVvgO1tgv+R31Hd16NBCs4D6/aiPNB+oPcckW0zeooKUJbMnDX6CfmY5/n3Z2TtceS7GOFApliEE8LrP/gkvg6Q4F3BPk5PvtfPYww17azU0lEQtS3A407ogGf4odF/6T7oHzK27LxJ23b6NE6EREjCTzU4qGeEeUPkPcfAgYCsm36/zQaoRo4MWEkequFtUlnoH+G0LBUEeW6yLZAT7r2VDKg4mtxxhrEEK4+RsOJiSSBp3RWaKg6Q2bgio3U58osahBYycxFP4ehsVHMyd5fVcf+jjofQubY2/7GtkHXHC1McYHZivSeVDuRtDyWjWGWTVzawf7kJgN2+2FnVNNFUr+XQlYIHyM+5Y9+vdI+UanRVpalu4qIyPtDxYgD+J2+Z4Rt077UGbozcyfBnspKbzsyS4va/5ErnEpFqBzBiopGfufsqKc4XmB4ivP1kt8k02jT7A6cKbcMfnzz1d/9IvrDulYnEzZdgL4eM0BsyYT0Tqx4/DkegOLjtyRCFZ8wQyIDbW9prJMcywkil4M7b2sYzIGPbe4X4boA7j7TMSd6F/pYFlwBAgnOr4L4s=Question
prXFaIL/Jzokz/kZ4mG0EdDKjLvNXGQT7PSvMKwaPCqE3K3X9NWNwd7Y/Svr862Usm+HVCLN9AGlTOeLKZVeh0THRAAiDkiulX43xNN7wZU70bJGtd39gnLcbTtCCtBIY8F2lt+Rs1IHipBCg0DfY/JakYfRbgnKcSbqulk+G1Z5JBuwWVb8NwoksV5N72RByGAP8QysMcBe/yXsSNpSqcI+VSmFVgq7eSWSXJ4fnAfpuG2lb38lCH8v9d0Ea15N4FRqltCCBTrOfoBsj8Jv29SSdNQ99Nu7kApXtcVNzn3kseDvp64aUB63ln8yDzyS6+DKCVjSXohOl8WOlZZH9kMP5stvDraWIzNqdjxINJVfQSWSGjiUJGESF1YxMPctEkiZx42bg+izIcuv83T/vBDXuyKQqzgcwoixZQwbnZPgbNinLxmsbvTbP6z2OkfakoeWe0wx3Ub5/+E/fXpw7zHceN0TDY0ilRFbY2lU4j9lL2Xt5wUQoyQptLTT4bZZ6sSjxtDIooqQw8rDRpYL0z4VKciAqdYve9XFnWf2MUT2woWmdJInCEMVFbMGkpP8O7LYchc1HZIYoIeOWae4fogAnyzQbe/qNk5xOiaLl/tZ1JMPQfDqLplbgQ7jbyMUZOXg1NeKQ6Oi13uDhS6We4w7tAka4ROhBAReTE5VDQ3h3jUAD6xCg5nHmXosRUDXWclTWB53FV7CNtmuCY/HtS86De+8//E51HrsxUvu5nWov6FL0n/ZS/O7c+GoD8c01ncxHqRzQ5MCFYfUWcUqciEFw4wPtsoWbmZmGrmbjoXaGBsuCUH+pVjk7IhYW/2oDEg3J36iArw/PARFhWchfzCMhTccQ4NEgyLwh+mxqvhk6pmCidRkEUvkPfQGeW6CfkA3+aJMU2NRJTTbppwHvV5XCrU2nn1ubTF00Ut0UYwMiPtZ2Ick/VYZ95GNUhIbQcOQIKIipLHpsV9c8MyEeEgHnAPSWj7Cbsf/pp8ek7W4MvJPygTZiAeAR3MDUiV1A5jZcSdhAClEGOZXR6QYveC5s5gxKyaHoHnJSmhZmJmMCaxc79gQpMEd3kgvNPTpUhy3GdJo/76GEcHuN9j2Er16armnOknvGdAJa1gUJWwoxVgSLTZ1rne1EgcJo6XO+9PfgPmU+yY4G0OvDdaWaRkI1Mxi94YKjVPz0t7RqqQ954Lb3eQOBUveUXJ1Gc+AcvdC5kkJgkSa9FGjep2VQvvSvSGN9G2sZvW5GvFZGQO8lH29GDdSjIUw7BG4S9FKcyCLAGpHju/AUAlYulpoiyzpuxZRajIEAdbzjz4DUha/QuSVW9L5f4tnxvDTVJgt89/NuwVSGajGRatx9qXFAo+z1KJKYOHPoCKdyyw1Hbtp1lh9/MXj1bWgEyZVaCKZwjXouO8EhfzF7A4Bg3VmAyEjSgJI2eCS2dPUHs39AdA5vY5XDh1vPbj2ZgZ8pb4NIpTewlgdE/ghT5ATqS/UKkI3hAOePbpyUrVSd7VGjoqOZsijty/AcGh35UkyrzWASafYzm3EjKv0AOuzwr073/rYa+yhOShDCEOMvrV5e75r5J9HB0SY9xA26wpMEwBX81fYeUiPeXBPZirwVQfKGWdbq8yM2mz0rlp1IiaCSq4vUAgMZkw2jmnbCSg8f4FT6Y+nlfUDURuE7+9IYMAB/ISa6lzZzRwM7lVM3e0IeDGCG5BcAozNMBj9XBQhBwemP2GwqrQ+mKYdq5wZH7G0sSI/PSu2RRnmvlOVh8G43eYj7sIHvkCQF1Q2vcwUgcM2Gm4NcG7yImLpcEpoaBX9RPN5KlB4d+qmK4A9dPY7joa0Ta968D9UUVuoemhk8HltbyCqZdXZFcpw4HQkSbb8QuCdGZeKybUBTdxbGXB9G6I2qUO68jZgx3xG99qVMjNYkRX1Wv0p7rk+MRZ9Rp8dZ9Yj6QE8/cmFEefDAXgYj8//KzaoxwYQ8qxbusliKAIY5ksf6Ws6JZi3UTPjf3E9WQgaf8ITo82SIipUv+bqLKDhblmAPBl7EVy1QOuyvoeXJuGgvRO8Q/1NWIqa6e/adfj5I4cFpyxOtfqqXkFGIoGRvBOQEZUHZGlEJz8dOie3ZoJncDKeCWiX+7t+ejKg09nx1zVdBeLzMpc221vUm4uz0VItQfroL2SlG/31z8dVOqmRzFz0prwRbfLF52UrrFzmu/QmcPdyf1fXv30v9XQcz0xRZAsLjYLBLnyszedEP8r3plZfCk8m5WGLWP+w2LyFu796AmflzhsfsJYsqlZx34osPbosBG8Rw6QKvFXVyQMaohs0SqRVGInrFvpnm+C/ivCOBE5qXgro2jlBLSLo61A4n7H4MFLM1zcc+xSfV+OT4jb37hv4/SiCoj2+2CgUYaH4s7BVXdHE+5XhWIXYEBJuiThNxyBMzQ1YI5tfNya4GT61LfVsoFWvem64OfjGmiJc4X6p1V3AH2trN0gFi2foDde0uOXEifcg5vLH3vhfR9D3cKjrFI/V47KiXWBZHMedHhHWWUgRYdwBYMRFG3vV3QgI/HJ8ZsqRkIdXk3FZ2UDBpEg3d4h+qV9FHSqOMUyx/1PGueU2YtTt/V17cvVP/5xpcmftRQgAL5vPdT0tzMuCupo9EewKb90sjxawAliG6bKswZv6JXt40QXyh8N57CmZuiehmtp2Q5tw3ds6P3I5IaPJntwy659hT1c2YW31uRUz95+YsSq/Ht0=Question
wRzJWd72gv8tF915jofPNoNlHdSWnocVXiCG5+mEQVMtVxbMzBBjHj+a5ECh5HgbG0olBH4XdYd3p2FVLkSd1kZvOauHrmRw1wPaSUpU53hElt+l0q5KtdNmB22PF1wrzKVoYKyOClc7dL0jKtAtkbAZbQBaisflanJ8ZgCZ6tM8swO0tsZUwNQU0AjUzyqxWoPEHDIbVNiAVjP4M+r2Hizh0w5k/UpEZuGebY7S1MiI7PXaW5sn4sKEEXuJHqPJDeAhO1Xk6C1qzPWn3iVTaiE5R+am0pvY2NYgdLB/2YDQ2KrQF1tPwXLkUVLQ8+B3S6zjwBaxHdCxi2qzqn0JncPDdAO99vmUjNjZXhCXRoOSBsCSdAjOAuAdmpy/WPryg2W5FD9++mYYYjyx4wM1ASM+WHXhTCtN+EFnUfI8rSpkir0oi9SAziSZSv/Y81QfDl4m8U/uaLyAnB2MHXPCK8jVWQuAP5S/iX8gXG+uXfkGIT2lJ/knYyBdECgisTnicsjP5omZfgM9/NICCjlwV2T50OadTQ6BYFy/13CX/N8erxbJespFl90s9HCAjZVdXJt+rDjqqJvX/RBMzOtb41JZkRmH42YkNh/IhfZp0DJzOVwbmTYpojur0NYe0K967PzxddyK5gzBCWb4osGgL060cjzcezLrHd8l2TO5QjrB3Zpj5fI78NkCjMx4nXkpJhgxgp38u+7ghu601uXnCHOup6VWqPOCEHbwi4crEBH8sTGHSIZoQvRoAuEoyFYZsb3PqNMau37cjwfS1wR9CteoZ+banZQDKKFE5ZCdp6Zf4vSuxYwOKj4KIzmV/RV5F5TczQb/MjDw+DXDZa3XwU7jKbBjDBjiWulHZDjH7PvTnzlzpfS5nCvtGSyAFrn4IgE3HryX1CCpGYfyS+YDSwJae32IBBX6t5jW+Ifnt0vDdd2sR5XCzyy4rjqyylEdZeTpLnoZLM4CrJ9d+PlN7YQ7JAHJKz17Cl30Uh5dqbEoTLibyL/V0ovX1TFHuTlh6nlC5vdQmFUEjM+KDTrQCAPlgAtcqZVdDTGewK28Ct+N7DMpq3mAWq/UZXujMpWXPCdXaYJ1u4JxtkxfVe+xeCwf4Ei0yqeSmq4gYqVoYKbsAsScUwHr2Ay0RZkMG4iyIJYfDh/cL1d71YKk69gwXmrqCCiVvnMU04ETKY0lvvawM6N4H6yBBxxWJ5fTPa8XSWY8j1WfpPqbBJYKzNf+YQAOFb2gjDg/gmjbw13/N4f8yb/5+JRw6TkT7NCLS/+eBS6B97zlYAAHh72F4kT3YuGD0hfVjkDVNDuFjVe96O1ccmKiDAWGDPJrhsXhcWJufyjRj7bLRl+/Gc3odTrD/C53FbPw5HysDoCKASbQtRIgN6GHgVo6XmWX/PoVENhJXBCulLt08yRvLvRZS3Q29KwHP24YW0kPf4JpT0r1oyHvAQHa3OWSwazhGQHVTeQ9RoSUgczIoq8/7QE99NsNW/5v20EgmSUG5nln4/leA6KC4gLBC0MWUvRMpchYcupmfFSmO0/HEHounvWCK41CW9KSn7fgnWL4INKvPOLHRaC5JAkNvaJPvvRlJFiBXcRZ3EWhD46pm6XTDRSn+1wTQkR2zRmWhxApkpJ1oR0LlJNncOWovGDNHq/sElYQvbvBHS4gCyz0zeeQEJVbLo8QCNtcIYA+y1G3wZoz/UmvfndQyBTCJ3zJK50rn7GDnvH3z6scSUcJniFQn57/vKU/M8t3CaZK8V3Kharrp14ulJ+aw5lo9hJyA7EOiasuj4BqZI+l1hRgbZ+dSSCQnsxYhAA+rlxbNCwzlyYk0HKBK8vRPA4Am3/uGfSlqZIdo/CiAYb0y7xpfNnANxE1S/JK/dNbQSrLRj631snWfX54ZKa6q5cIE2mTfaS+5+e1HNCpzQpCQXP95Qc0+NOZh2Nb85fL6FTHg/Kz3qwRzxRqkd2rQrZBqVmlNMti7+8z2W7BFB63dqzKmvMsBPxamS4GF5lnWwJRR3Lq7enEXUa0+7OceU6djTHU5Y/EhHLBEgdwl8MUMv2S8FY7XvhtLeB6DnT5w/lDbg/ubsRM8qifNSgK7nZ8NjgCkvMUMNfrdIwJbI6xeUPD77fJQd8oJT9/4c0YCV7VHuzy8wmNZdij6xRK6oFMEPOXWA8PuW8PQ7L7hfBD7ZRM8Yirx96mA/Ys+gl70vMpP59chLgm4DGHb9XM1tTquqseNTI9wVigwgppeF0ShGVdcgIs+VuELp7Ae5Ibz3Xkl5UYU9/4PmuDs1ytnsD/86r96wsBpJQF1Qfj/mCD7goll2k2eJTQloVXAn4poYwD4gnm/JN3En6/ojIjkbo34N43FV8hbLQpy53O++XEw8rjRm15bxVDQgsyL+32Vy+/2P5dgGbuCOX94BC7GLQj8GLjmMLRtH7GFub0xZeZPPDK9eLisbF4vFrBUxaI2XcIy2zEEtAK5HcUyJJoI+WX8Szvq8djCGtCS9lRNG/ikE6o17vID2PnRjNDL7M0F8us82EDuUjWWf7XDWbIbl9Q4/e9xhaN6I/JHb7sb9rxv1y2Wo5xl6zjckzodrJgHSfDk9EpaCsU7+b20pGcRI4uDC3DgmGOqBwSmnbAXQyr62Y+jEoN4TWEOw9iyI2RAtvlDQmJrBi1EZyliY3N/eOOT1otJXBzgexq1zUMo6HBp9OlQtM3DmC4InGD06KV2CAQRbO+m0EVHWfM6RUDcN9AmijyuQ==Question
TIAZeWMLCDr4InodfdbSI2iJTDRbOxIxmAnd6tdulNRcwJpKjmRGzjn7o9FnhnBZyIPeEj3AICtPWbK47RSuIHbp5PcroOGZPwzEcL8a1Ph9sWxsSPBpoK2gQLhw2gL7/LvfRbrD3X+8GCE2WNrecvU+5j5MvHC6eNTeC3kUx3h+b5Kl5pEIelxUBHeRYYTOCygGori9ZEwRMzCYY3coj6XBHXxXC4cuL6qArQb5hnHazx/O83RvBWLfnBjRudjGn6KaVb7lS883+7QSlEPP6IcIoe63kORMKgd2XUUJnRwGGh33iKqIkq2TzRCbo96tUimS3rV0O+xWI8HmOBbPygK/5kYp1bvtFtcJap4N6axcfAAa+u7BpAZlymFK1JmD13qfSfsY60CDCmZawCTotwDymluKK5y4cgKcC5l7UoECZAq8pSXhcK2xgXF9bBzi69BArn7Eb66K0Ee/9nwBJaiY7O9L8JkBU5cl35xBSTzf7HjMLcGoeVm2dtIu+hLURqTIJltoLTBXxr/0fFuhTOASFs9NG6XVyi+31vrgbNqH9DPH6JSM4SdWSbxdJu4W+81npiSqwFLvHu4PzSe3EL8UyF7YG4nQHAawM9bWcVutqO2GVXmcB4umvdza9wmrk4xWgZ1fp5ibIyHibwyr+bRrhVDrBFuW49PhxTFY54P8OAy+YZ1Co9FvkOB3GqUFPaNsEk9Gbz8wsrbncQAaOs17JY836/zqr+iyiIHFOyh4rcEk+Bi3SrT/8JZfnh7k/lI4BPshDsmOUdLqPMtR1tCBsrShnu6J+4Yh/96+VADmE5SDXBiUo4XQi/2ksK7E1jyfkVCOrSuMe9AdyUP661pcohzJpDn37yn/fVmR7eGfTFtIRNhMn1agvPmgJTLZJB9kRzmPi9SbgBwsPk2MRrEwV2m3QHDrvWzuMu5BHD1oMhaIPDBX5LoKs1mhVFa4RRNcyjyHCrmwfNKjqCTG0m30B/hQ0vfmc2FH3NluXDlfZzMZ0tLLkINP1CSjUYPi8A+G7wgrEi4QscKehLSvFx9ZHmnqB197LVmbT0OaqHwoL+bl4FWLR4+6olU2ofbC8GknoEEeSPPOCtiF+3OZkarNd8ltCJqIo+MFktOWbPCotW/Sqb6C4zLQmn+2t1Nc0kJekQCdcOLubzdI8H8VrvlSw89BhQ0zh/zkWNnVY3x0HLeOIL9EcZkm2IgzRmLFyWvfL3Y27kfUBe5TmWfEoIS5f40H0kukvafCUuksKAiNIpDs9xtJyvo/JFzJOqf14Dtocrzpialim2S9g1aGuqeadlYajmb7ZC3sdlHtKdxd/fkzqUkzJ0VCFQBU1UjI6UwRjqyEgoTSbjxu8wTHVSpdxdYa/EpgoE+5Nhm5zvMnY7TR5PhsDK8dhDxqcRQNDhFf8jFjWzB/lKsl55d1GxCVLMm5Ng4BORtTPd9eIO6zyaOF4wrhpuJj7kSo9dOb7Io68baXam7uMZVcnDycq8ASn/DRDqTmXVImSMKk+TbZGU6Cgd1sSsHsppE3JCIz3hwOKoEmd6hB/F7q5rWSJbC5ghj3Ue1zglyZ/sRLiwq8iDH/caO5qqJOTZSc/AesD43v1awiKhKPDo9CRZZsJKL182GCFduEBg3zjnVUwnU/sFQo2/zYCOtTtpYiNchiLZQW6WQSDTwlCfRlK8gZO9EqUrCbkdnlaYTVsY9+CZWNH62VZEjACRrqBTh5DEDeHc5zs9HOg6Pn9yh/Ut9ddIwhzORsvRbEekjSz2QIQ6zuM2UT6Vj3Q5qlMfJ/yN0aIvMfsfJOf88nM7/a5UTTFDMU5IxrWr00VsEbcfLOh3hTU/FAMd1hJiNzsvFoWwtscfAtAJ62fC58heTxDNhsvA+z0ytY7BOUYQmdgbt1jlVAQny/Ngs0a2NcWCK5PTWA/jvm5YgdgJ1vgk2QUJaNWDAotpHyJ65GIf2DRtMlPbOi+8ueIda3qS7DEKXFkBo1FNuoZyYlCrE0fVwZOIYYc2ciCenz4BokSo45stYzEHvhrZMfniLJyu4er3KxCxJwdp/G+JRJZvyNMu2Fn7UpShy/MHDDpJ+3XcCNJ4WB4K5lSPe4Kb/aiTpDvWmPJ1ekcYs8erMKUyrBOg+xEFQk+rcCQ10OpXSoK2i5qnuT8bEjUAwLiiRh8eGOGmre6UwBbRR6k+nkWpdNeOuNIKVJ+YiHAQZc815rXzs1bH4laX5ydkmoN5ehD7HTD0duKeiGVulY2ZKg08sHHiWL0UXRK1iRddrdUCVsvLzRF5N2+D+T4ZmrP4aEu5G1xPGRWOeG1KHwsqXJYit8cwpzx0jztUIXy7Zi+aOM5nRf18WWNggBPNlLFm0hfNetGCYwp+AM1HUi2+zdYQMKKHS11kCBfvoEb1OzxIhVUa8NaTpa6N98f1akuJKJlG+yIqWFJ57w/M7YtlTV7kk+CQ/04i/VEB1sHeulxIc3QEIXfNaNKvAzdygdZGZerPrh3fPNGqyE72V2Bg0q6H8CrT0Fl9OSDb62IT+TIAHyVgfdbLsUdTmUUVtuUkzchPo2E3WGkwz83onWWTPE8GYUgG/MF9BiPuVYeiwAG1SpKCn0n8lu4fQeQxuWcJaFZXDl4nQuTJoKN7MdO9AnG0e0o5oXAzxe0967M5qy8IAzGAwijZ8UTu7aDgPzQEOptoJ45B7ZDbZZ1e4smTT2yeXMt/8S4CdhmrVh0zUKqcosJWzTz1Km9UZHjxjceShvEgbB5LJAG4nHXkyP99Xv6Ow=Question
8RR+SI4NmBzH5qwZFgeBKGXP9B42YEnYqt5JoZBMttG86RyED54PiKy3wmsXQU43gWLYg70ZcotO8KKMxnlivICktSqSUA0E3NumdFAho5VsrcGNOQ4ga9k8FGDKJQTyec+xTeyRvOQRto1WlEXmhT5pDM+d3Wga7KSaz2cozjJJcvyxfXw9Mh55SARYL+qhK38mZ+uDHw1WBRRROa+t/+dtVRU1ylmCX28DRYARIZvrhFnoJ7HKzk1dmYzbNzqTqATTOssfWoClrRJmAqZdwScl8T2jSBreagE8ziAdz5HfzGjCwODfOntz4iPKb2XBZAExN/PC3lSEHVdiUlZVzptzVsUSas9MNn5Gi5qNUg7MfDXTrfEmy67kO96HIdrku1qmCkDC+QL+sVCiIZBLl5dMBhDXQkx8jiKdUCK42UV85L3SeoNb7tQjWeWi2lk0ctpaR3JYUnBiF14Oiq7UMc+GYcbPwpUWQVAvheL0dmFvfnkvlqEbpJZVg7fmhdxG2Xsli6+tkHrCY/V0F5ie/KBlG7qD2tkcvhnNebfAm1TXhwtsyBc8o6H1gp8UMlbQO7L8VkTQF/CNOwSiVrh1Vrx5AzQI/TIfRBNy15E2nQbIEl7PrUTfXxakDeCW6tk0Dyq6He3CYJC/4PgTucivL6vyPKG4TGdwbXzFKHFFOmROF4tzxoocFTY5OIFyXhp/OMKjUfKilFffoexjHLLAcjlTCp8V6Wbzhcfs0kO7DNPKB7qvurLVfxsdcus4vPh7kKF7ulVRCpDWs6u7aqL72pNLz3ceSc34xtD5pTsKuUNEwfy9/CWmAFhRHUEVtFHRB9k5Umaro/3xG/6NuhM+kmlB7WtS9X79BHkcWhQc4Em/ugyOtUWBIUunGBQW6BXQvrMiNEzHm/zcWrbVOBqNmhnpkerbZXY8T1shaoZ+rI66aBiSKfiVyZV/guDp+rEd6EqOH8vrDM42Mm5gcYrgz4CjGn1bJHL8sSwjUW9sltKTkPHHtWIjoAK2xuJXVgkcjDvW7QlxB4xXeAgMZkqeCLDaZ+XFASVcjDdV74gzCiqgdvHcFBK20g1rYBalVjKHln58ptjtINK+bs3lXceG2yBAzoR5U1l2JjBq12wDdiZIi/0j/jZcyWRdaMYH0FbG+jpQW6TYEHloQUoccg8DgGyLw3okMI+SuSaMf4isn7wmtibQ25TvDHVooULEgocBoZRK0WaxW8ekCNSCTmFbdjCs63Mkccv2Mrs6va4wvcGbb+DkKjqsH30LA8+gdeW/uDx+6IaA3D/zplUCmb70HlvL4HLHfyAVHJGwclIH53HH4X0u5caNcnlf2yXKFC4VfSrNzpVqExCdnKhV3wa+50MserLmQvLc/AjjY3MrxIQ/HN8Q1ObVfUhYEc5vExNuiH0N5p4eVdoAp7X/YOGyBqE7SRbOB+pDRkZd1yU6hUZNk6jOEv3OxMIz+u9uy6DD6OWtwvD8JFPeTtWbolgnou1GRTeCm4W5r2U/YQicilE3EhiVsHA61B5B4tp0WjjAYz61Bg/EL0AVIQQEKygB/2Pl+dTpwzF0ye3ivayoJHkq2XdnGwseAvjxlZyBcO/V9N3awEKAm1IhjMFkAuzXkKcpYzsA0viZYkYdujWB1pSgonMVOC8VR6Xt13iwRs5wE1FD1PDK0+LiiGi6JWliJewIXj9GgLZSLHDE9L+nrIUbklm/aVxcaQ65Doh4UrFGKb7FJSeIU32iY1nlmPFP42c+lhIdaydleSIxZvIfaGT3vgOXzFRB+fV/aPXUfNyZlNdlGeSL4mqK/HmTc2KCZ/d+/xb+bRo+3axoH1pbw9IDdNmN+CJ9dBW6baJoNdy7CBWVQzpk0xVOJsrXCg8LdkZHv0DEPsiUZcINF7ZYyQZH5DLd3CY26GAI+y+JlvlCYqf/1WVOE69969Ej/tp3s9UpIdot5T1IrnJNInKujA69kucOfefTLYZS4uYrp8TlRBpKPApJwhPDH0mDfZo7iY+r1adOmp37KJFyHJUshhK+RZzo1cfFGirumUB0q8FzK+Z8ZP8oUYkM3/L6F5Z3HJB2ceASvrxeiwhpgbHVmdW6OJYX7nki54aUnr4LRkOJ8l8xPbInX9WYawSybIT7v1FD4plUk0CGkZygoFFuPlO0hTfHkAfWR1FDFvukLF8qa7ir+JYObwwh1h2ozc9Y0ZUAo+KvlUVWgo4cltymfcFuwAGUyt1uiXMxA0O56fHyuMbpvxtnNyQSBn8ZRbTxJwRaO2qSZx7ZL1ZhOg8Vhf4avR/yNQI5DTXFIvfykz5bjcWyBo4EBqImpRGQo45JKKItp15gKDl2YYPEckoNj763rsaRtAogMCOimSfhN15wmComp6UY3Rk0jYAdPtT3zY4ExmcZ0K4gsBJMAe50B4csiFYzEHJc7O4VTGmVpFDTT8SUwDjSY5+QiM9zKcbZ0LlNCW7/x4DgzXfiC+YYZl4joiOn07FmztxtMJG5gYVpnW8uwaf23zQL9ZXI7ne+qa4L3nwFZqR+/Zyp1rtBVD4AfKpWW2b0PC+i8E0t6AK1lSEmq1bed2N9TDGfcq3ggc/865Ye61gwhFaKpfiOZ3fueY0pG4BCeu0W+4jHfQJcKeti4ezeqiHiL9p/45RiTFmE29GC/dWief7T3qoX4Ac377l4wf6glGbdIGNw7w9VFvccp7/NUITjkkkbgJc2gX0MdHL31Tfk1Hj7M+kTtN/SXMwdllvL+D4z1FjUG+KR7:04