Chapter 9. Chapter 9 (Chapter 19 Macro)
Step 1
Work It Out
Chapter 9 (Chapter 19 Macro)
true
true
You must read each slide, and complete any questions on the slide, in sequence.
Question
According to Chinese government statistics, China imported over 1 million cars in 2012. Let’s see what would happen to consumer and producer surplus if China were to ban car imports. To keep things simple, let’s assume that if car imports were banned, the equilibrium price of cars (holding quality constant) would rise by $5,000.
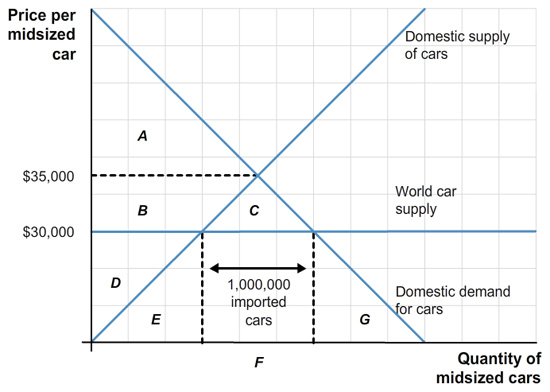
Correct! Total gains from trade when imports are allowed equals domestic consumer surplus plus domestic producer surplus. Consumer surplus equals areas A + B + C and producer surplus equals area D, so the total gain is A + B + C + D.
Sorry! The area you selected is a part of the gains from trade, but it does not equal the total gains from trade. To review how to determine the gains from trade, please see the section “The Costs of Protectionism.”
Step 2
Question

Step 3
Question

1:49