Chapter 12. Chapter 12

Step 1

Work It Out
Chapter 12
true
true
You must read each slide, and complete any questions on the slide, in sequence.

Question

Now let’s take a look at the equations for the marginal cost functions that are graphed in Thinking and Problem Solving Question 3, and see if we can combine them into one equation for industry-wide marginal cost. This is what the two equations for the graphs in the question look like:

MC1 = 2 + 4q1

MC2 = 7 + 2q2

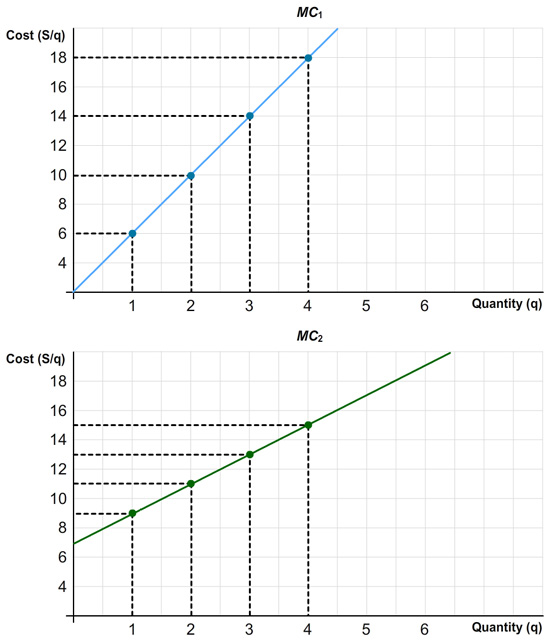
The figure has two plots. These two plots show the quantity (q) versus the cost (S/ q). The horizontal axis is from 0 to 6 units, the vertical axis is from 0 to 18 units on both plots. The MC subscript 1 on the first plot is an increasing line passing through the origin and the following points: 1 and 6, 2 and 10, 3 and 14, 4 and 18. There are also four horizontal dashed lines and four vertical dashed lines connecting each point with the vertical axis and the horizontal axis, respectively. The MC subscript 2 on the second plot is an increasing line passing through the following points: 0 and 7, 1 and 9, 2 and 11, 3 and 13, 4 and 15. There are also four horizontal dashed lines and four vertical dashed lines connecting each point with the vertical axis and the horizontal axis, respectively.

Can you create an industry marginal cost equation that shows MCTotal as a function of qTotal instead of just q1 or q2?

First, solve both equations for q and fill in the missing information. (When you input your answers, round to two decimal places if needed. For example, if your number is .3490, enter .35; if 8, do not enter 8.00.)

q1 = O/5zOqbS1ag=MC1 − 9QTCBFxAkBk=q2 = 9QTCBFxAkBk=MC2 − brVrJl3J7nE=

3:12
Correct! Solving MC1 for q1 results in q1 = 0.25MC1 − 0.5 and solving MC2 for q2 results in q2 = 0.5MC2 − 3.5. Note that they both have positive slopes and that q1 has a relatively smaller slope. We can check our results by plugging in numbers from the graph and see if they match the equations. Plug MC1 = 18 into q1 = 0.25MC1 − 0.5 to get q1 = 0.25(18) − 0.5 = 4, which matches the graph. Plug MC2 = 15 into q2 = 0.5MC2 − 3.5 to get q2 = 0.5(15) − 3.5 = 4, which matches the graph.
Sorry! Make sure to check your answers. Take a value of marginal cost from the graph and plug it into the corresponding equation to see if the equation provides the same number. To review industry marginal costs, please see the section “Invisible Hand Property 1: The Minimization of Total Industry Costs of Production.”

Step 2

Question

Now, replace MC1 and MC2 with MCTotal, since Invisible Hand Principle 1 tells us that marginal cost will be equal for all of the firms in the industry. Next, write an equation for qTotal, which is just q1 + q2, by filling in the missing information. (When you input your answers, round to two decimal places if needed. For example, if your number is .3490, enter .35; if 8, do not enter 8.00.)

qTotal = G0+n1+REjHA=MCTotal − h4XZagboIgc=

Correct! If qTotal = q1 + q2, then qTotal = 0.25MCTotal − 0.5 + 0.5MCTotal − 3.5 so qTotal = 0.75MCTotal − 4.
Sorry! Make sure to check your answers. Take a value of marginal cost from the graph and plug it into the corresponding equation to see if the equation provides the same number. To review industry marginal costs, please see the section “Invisible Hand Property 1: The Minimization of Total Industry Costs of Production.”

Step 3

Question

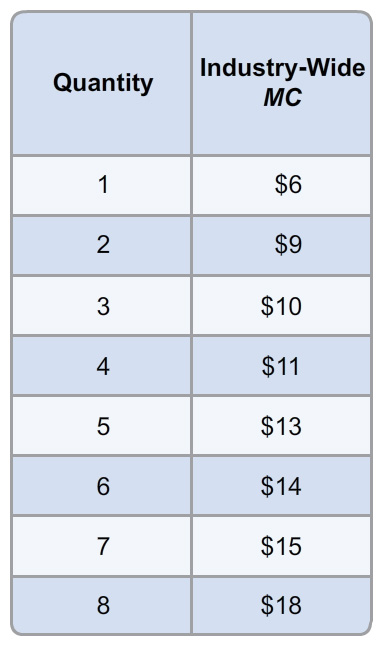
A table with nine rows and two columns. The column headers are Quantity and Industry-Wide MC. The values in the second row are 1, 6 dollars. The values in the third row are 2, 9 dollars. The values in the fourth row are 3, 10 dollars. The values in the fifth row are 4, 11 dollars. The values in the sixth row are 5, 13 dollars. The values in the seventh row are 6, 14 dollars. The values in the eighth row are 7, 15 dollars. The values in the ninth row are 8, 18 dollars.

Finally, solve the equation for MCTotal to create an industry marginal cost function from the cost functions of two different firms in the industry. You can check your work by plugging in quantities from the table (based on your answers for Thinking and Problem Solving Question 3) to see if the equation generates the same approximate number. Note that the equation assumes you can produce partial units at either firm, whereas your table was based on the assumption that only whole units were produced. Fill in the missing information:

MCTotal = [SLOPE]qTotal + [INTERCEPT]

MCTotal = FB:*1.33qTotal + xlSoIpNdi90=

Correct! If qTotal = 0.75MCTotal − 4, then solving for MCTotal leads to MCTotal = 1.33qTotal + 5.33.
Sorry! Use the provided table to check that you have the correct equation. To review industry marginal costs, please see the section “Invisible Hand Property 1: The Minimization of Total Industry Costs of Production.”