Chapter 16. Chapter 16
Step 1
Work It Out
Chapter 16
true
true
You must read each slide, and complete any questions on the slide, in sequence.
Question
Prisoner’s dilemmas are common in real life, but not all real-life games are as dismal as the prisoner’s dilemma. One game, known as “stag hunt,” describes situations where cooperation is possible but fragile.The philosopher Jean-Jacques Rousseau described the game. He said that a lot of social situations are like going hunting with a friend: If you both agree to hunt for a stag, then you each have to hold your positions near each end of a valley so that the animal can’t escape. If you both hold to your positions, then you will almost surely get your kill. If one hunter wanders off to hunt the easier-to-find rabbit, however, then the stag will almost surely get away. Rabbit hunting works fine as a solo sport, but to catch a stag, you need a team effort.
This is the usual way of writing the game:
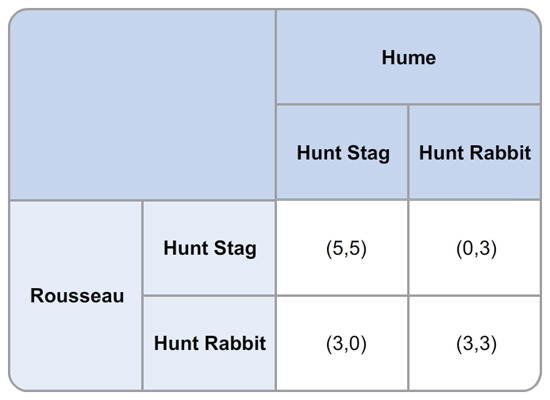
If Rousseau is quite sure that Hume will hunt stag, he will .
Correct! From the table, we can see that both Hunt Stag and Hunt Rabbit are likely outcomes, but Hunt Stag is riskier since Hunt Rabbit has a guaranteed payoff, implying a level of trust is required to achieve that outcome. If Rousseau is “quite sure” that Hume will play Hunt Stag, that should be a sufficient amount of trust to make that outcome feasible.
Sorry! Consider Rousseau’s best response in this situation if he is quite sure that Hume will hunt stag. To review how to determine the equilibrium of a game, please see the section “The “Best” Product May Not Always Win.”
Step 2
Question
If Rousseau is quite sure that Hume will hunt rabbit, Rousseau will .
Correct! From the table, we can see that both Hunt Stag and Hunt Rabbit are likely outcomes, but Hunt Stag is riskier since Hunt Rabbit has a guaranteed payoff, implying a level of trust is required to achieve that outcome. If Rousseau is “quite sure” that Hume will play Hunt Rabbit, that would be a sufficient amount of trust to make that outcome feasible, so Rousseau will choose the less risky option of hunting rabbit.
Sorry! Consider Rousseau’s best response in this situation if he is quite sure that Hume will hunt rabbit. To review how to determine the equilibrium of a game, please see the section “The “Best” Product May Not Always Win.”
Step 3
Question
There are two Nash equilibria in this game. In the first one, Rousseau while Hume . In the second one, Rousseau while Hume .
3:16
Correct! From the table, we can see that both Hunt Stag and Hunt Rabbit are Nash equilibria. For example, if Rousseau chooses to hunt stag, then Hume’s best response would be to play Hunt Stag. If Hume chooses to hunt stag, then Rousseau’s best response would be to play Hunt Stag.
Sorry! Consider Rousseau’s best response for each of Hume’s strategies and then consider Hume’s best response for each of Rousseau’s strategies. To review how to determine the equilibrium of a game, please see the section “The “Best” Product May Not Always Win.”
Step 4
Question
Of these two equilibria, economists call the “payoff-dominant equilibrium” and the “risk-dominant equilibrium”. The is the biggest risk that might push someone to choose the “risk-dominant equilibrium”.
Correct! The (Hunt Stag, Hunt Stag) combination of strategies is payoff-dominant while the (Hunt Rabbit, Hunt Rabbit) outcome is risk-dominant. Remember that payoff-dominance means that the outcome yields a higher payoff for each player compared to the lower payoff equilibrium while risk-dominant implies that the outcome is less risky. The more uncertain a player is about an opponent’s actions, the more likely they will choose the risk-dominant outcome.
Sorry! Consider the two equilibria you found in Question 3. Which of those would be more likely if players felt there was a great deal of uncertainty regarding what action the other would take? To review how to determine the equilibrium of a game, please see the section “The “Best” Product May Not Always Win.”